Main Content

interpolateStrain

Interpolate strain at arbitrary spatial locations

collapse all in page

Syntax

intrpStrain = interpolateStrain(structuralresults,xq,yq)
intrpStrain = interpolateStrain(structuralresults,xq,yq,zq)
intrpStrain = interpolateStrain(structuralresults,querypoints)

Description

intrpStrain = interpolateStrain(structuralresults,xq,yq) returns the interpolated strain values at the 2-D points specified in xq and yq. For transient and frequency-response structural problems, interpolateStrain interpolates strain for all time or frequency steps, respectively.

example

intrpStrain = interpolateStrain(structuralresults,xq,yq,zq) uses the 3-D points specified in xq, yq, and zq.

example

intrpStrain = interpolateStrain(structuralresults,querypoints) uses the points specified in querypoints.

example

Examples

collapse all

Open Live Script

Create an femodel object for static structural analysis and include a unit square geometry into the model.

model = femodel(AnalysisType="structuralStatic", ...
                Geometry=@squareg);

Plot the geometry.

pdegplot(model.Geometry,EdgeLabels="on")
xlim([-1.1 1.1])
ylim([-1.1 1.1])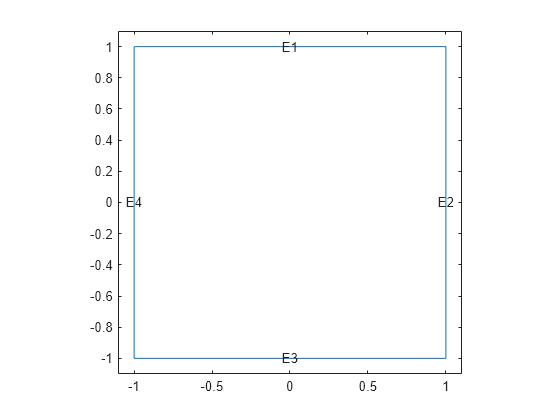

Figure contains an axes object. The axes object contains 5 objects of type line, text.

Switch the problem type to plane-strain.

model.PlanarType = "planeStrain";

Specify Young's modulus and Poisson's ratio.

model.MaterialProperties = ...
    materialProperties(YoungsModulus=210E3, ...
                       PoissonsRatio=0.3);

Specify the x-component of the enforced displacement for edge 1.

model.EdgeBC(1) = edgeBC(XDisplacement=0.001);

Specify that edge 3 is a fixed boundary.

model.EdgeBC(3) = edgeBC(Constraint="fixed");

Generate a mesh and solve the problem.

model = generateMesh(model);
R = solve(model);

Create a grid and interpolate the x- and y-components of the normal strain to the grid.

v = linspace(-1,1,101);
[X,Y] = meshgrid(v);
intrpStrain = interpolateStrain(R,X,Y);

Reshape the x-component of the normal strain to the shape of the grid and plot it.

exx = reshape(intrpStrain.exx,size(X));
px = pcolor(X,Y,exx);
px.EdgeColor="none";
colorbar

Figure contains an axes object. The axes object contains an object of type surface.

Reshape the y-component of the normal strain to the shape of the grid and plot it.

eyy = reshape(intrpStrain.eyy,size(Y));
figure
py = pcolor(X,Y,eyy);
py.EdgeColor="none";
colorbar

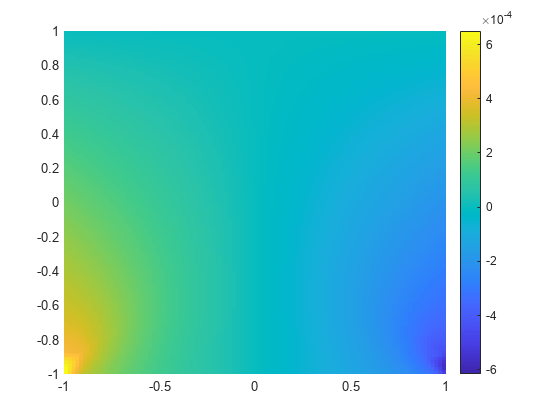
Figure contains an axes object. The axes object contains an object of type surface.

Open Live Script

Analyze a bimetallic cable under tension, and interpolate strain on a cross-section of the cable.

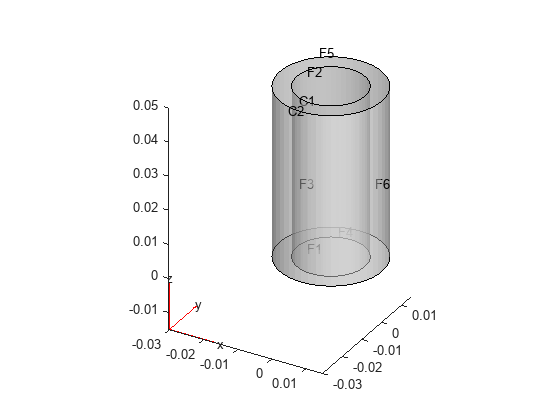
Create and plot a geometry representing a bimetallic cable.

gm = multicylinder([0.01,0.015],0.05);
pdegplot(gm,FaceLabels="on", ...
            CellLabels="on", ...
            FaceAlpha=0.5)

Figure contains an axes object. The axes object contains 6 objects of type quiver, text, patch, line.

Create an femodel for static structural analysis and include the geometry into the model.

model = femodel(AnalysisType="structuralStatic", ...
                Geometry=gm);

Specify Young's modulus and Poisson's ratio for each metal.

model.MaterialProperties(1) = ...
    materialProperties(YoungsModulus=110E9, ...
                       PoissonsRatio=0.28);
model.MaterialProperties(2) = ...
    materialProperties(YoungsModulus=210E9, ...
                       PoissonsRatio=0.3);

Specify that faces 1 and 4 are fixed boundaries.

model.FaceBC([1 4]) = faceBC(Constraint="fixed");

Specify the surface traction for faces 2 and 5.

model.FaceLoad([2 5]) = faceLoad(SurfaceTraction=[0;0;100]);

Generate a mesh and solve the problem.

model = generateMesh(model);
R = solve(model)
R = 
  StaticStructuralResults with properties:

      Displacement: [1x1 FEStruct]
            Strain: [1x1 FEStruct]
            Stress: [1x1 FEStruct]
    VonMisesStress: [23098x1 double]
              Mesh: [1x1 FEMesh]

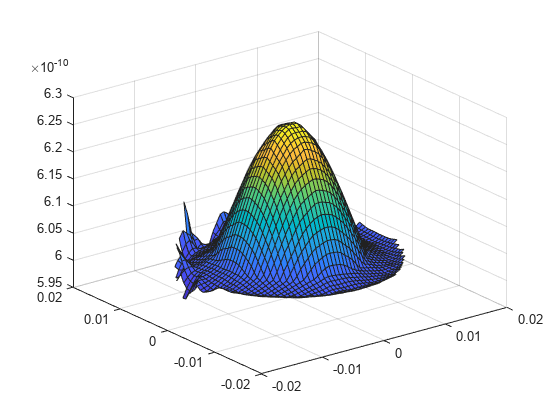
Define the coordinates of a midspan cross-section of the cable.

[X,Y] = meshgrid(linspace(-0.015,0.015,50));
Z = ones(size(X))*0.025;

Interpolate the strain and plot the result.

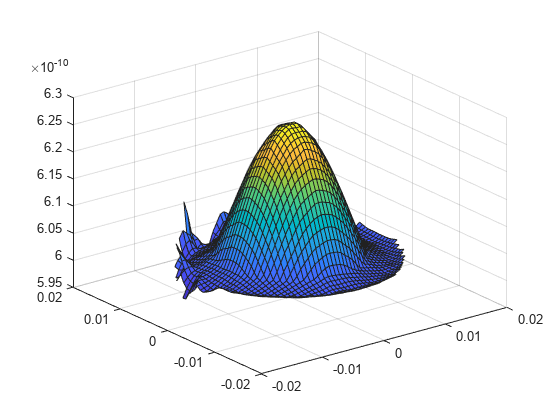
intrpStrain = interpolateStrain(R,X,Y,Z);
surf(X,Y,reshape(intrpStrain.ezz,size(X)))

Figure contains an axes object. The axes object contains an object of type surface.

Alternatively, you can specify the grid by using a matrix of query points.

querypoints = [X(:),Y(:),Z(:)]';
intrpStrain = interpolateStrain(R,querypoints);
surf(X,Y,reshape(intrpStrain.ezz,size(X)))

Figure contains an axes object. The axes object contains an object of type surface.

Open Live Script

Interpolate the strain at the geometric center of a beam under a harmonic excitation.

Create and plot a beam geometry.

gm = multicuboid(0.06,0.005,0.01);
pdegplot(gm,FaceLabels="on",FaceAlpha=0.5)
view(50,20)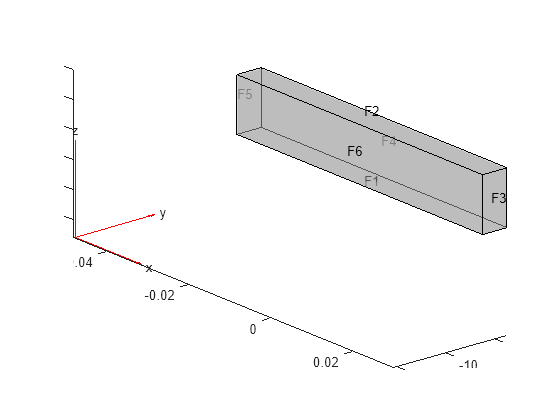

Figure contains an axes object. The axes object contains 6 objects of type quiver, text, patch, line.

Create an femodel object for transient structural analysis and include the geometry into the model.

model = femodel(AnalysisType="structuralTransient", ...
                Geometry=gm);

Specify Young's modulus, Poisson's ratio, and the mass density of the material.

model.MaterialProperties = ...
    materialProperties(YoungsModulus=210E9, ...
                       PoissonsRatio=0.3, ...
                       MassDensity=7800);

Fix one end of the beam.

model.FaceBC(5) = faceBC(Constraint="fixed");

Apply a sinusoidal displacement along the y-direction on the end opposite the fixed end of the beam.

yDisplacementFunc = ...
@(location,state) ones(size(location.y))*1E-4*sin(50*state.time);
model.FaceBC(3) = faceBC(YDisplacement=yDisplacementFunc);

Generate a mesh.

model = generateMesh(model,Hmax=0.01);

Specify the zero initial displacement and velocity.

model.CellIC = cellIC(Displacement=[0;0;0],Velocity=[0;0;0]);

Solve the problem.

tlist = 0:0.002:0.2;
R = solve(model,tlist);

Interpolate the strain at the geometric center of the beam.

coordsMidSpan = [0;0;0.005];
intrpStrain = interpolateStrain(R,coordsMidSpan);

Plot the normal strain at the geometric center of the beam.

plot(R.SolutionTimes,intrpStrain.exx)
title("X-Direction Normal Strain at Beam Center")

Figure contains an axes object. The axes object with title X-Direction Normal Strain at Beam Center contains an object of type line.

Input Arguments

collapse all

Solution of the structural analysis problem, specified as a StaticStructuralResults, TransientStructuralResults, or FrequencyStructuralResults object. Create structuralresults by using the solve function.

x-coordinate query points, specified as a real array. interpolateStrain evaluates the strains at the 2-D coordinate points [xq(i),yq(i)] or at the 3-D coordinate points [xq(i),yq(i),zq(i)]. Therefore, xq, yq, and (if present) zq must have the same number of entries.

interpolateStrain converts query points to column vectors xq(:), yq(:), and (if present) zq(:). The function returns strains as an FEStruct object with the properties containing vectors of the same size as these column vectors. To ensure that the dimensions of the returned solution are consistent with the dimensions of the original query points, use the reshape function. For example, use intrpStrain = reshape(intrpStrain.exx,size(xq)).

Data Types: double

y-coordinate query points, specified as a real array. interpolateStrain evaluates the strains at the 2-D coordinate points [xq(i),yq(i)] or at the 3-D coordinate points [xq(i),yq(i),zq(i)]. Therefore, xq, yq, and (if present) zq must have the same number of entries. Internally, interpolateStrain converts the query points to the column vector yq(:).

Data Types: double

z-coordinate query points, specified as a real array. interpolateStrain evaluates the strains at the 3-D coordinate points [xq(i),yq(i),zq(i)]. Therefore, xq, yq, and zq must have the same number of entries. Internally, interpolateStrain converts the query points to the column vector zq(:).

Data Types: double

Query points, specified as a real matrix with either two rows for 2-D geometry or three rows for 3-D geometry. interpolateStrain evaluates the strains at the coordinate points querypoints(:,i), so each column of querypoints contains exactly one 2-D or 3-D query point.

Example: For 2-D geometry, querypoints = [0.5,0.5,0.75,0.75; 1,2,0,0.5]

Data Types: double

Output Arguments

collapse all

Strains at the query points, returned as an FEStruct object with the properties representing spatial components of strain at the query points. For query points that are outside the geometry, intrpStrain returns NaN. Properties of an FEStruct object are read-only.

Version History

Introduced in R2017b

expand all

See Also

Objects

Functions