Main Content

interpolateStress

Interpolate stress at arbitrary spatial locations

collapse all in page

Syntax

intrpStress = interpolateStress(structuralresults,xq,yq)
intrpStress = interpolateStress(structuralresults,xq,yq,zq)
intrpStress = interpolateStress(structuralresults,querypoints)

Description

intrpStress = interpolateStress(structuralresults,xq,yq) returns the interpolated stress values at the 2-D points specified in xq and yq. For transient and frequency-response structural problems, interpolateStress interpolates stress for all time or frequency steps, respectively.

example

intrpStress = interpolateStress(structuralresults,xq,yq,zq) uses the 3-D points specified in xq, yq, and zq.

example

intrpStress = interpolateStress(structuralresults,querypoints) uses the points specified in querypoints.

example

Examples

collapse all

Open Live Script

Create an femodel object for static structural analysis and include a unit square geometry into the model.

model = femodel(AnalysisType="structuralStatic", ...
                Geometry=@squareg);

Switch the model type to plane-strain.

model.PlanarType = "planeStrain";

Plot the geometry.

pdegplot(model.Geometry,EdgeLabels="on")
xlim([-1.1 1.1])
ylim([-1.1 1.1])

Figure contains an axes object. The axes object contains 5 objects of type line, text.

Specify Young's modulus and Poisson's ratio.

model.MaterialProperties = ...
    materialProperties(PoissonsRatio=0.3, ...
                       YoungsModulus=210E3);

Specify the x-component of the enforced displacement for edge 1.

model.EdgeBC(1) = edgeBC(XDisplacement=0.001);

Specify that edge 3 is a fixed boundary.

model.EdgeBC(3) = edgeBC(Constraint="fixed");

Generate a mesh and solve the problem.

model = generateMesh(model);
R = solve(model);

Create a grid and interpolate the x- and y-components of the normal stress to the grid.

v = linspace(-1,1,151);
[X,Y] = meshgrid(v);
intrpStress = interpolateStress(R,X,Y);

Reshape the x-component of the normal stress to the shape of the grid and plot it.

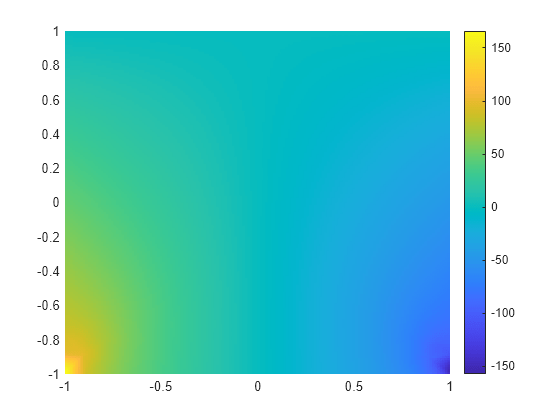
sxx = reshape(intrpStress.sxx,size(X));
px = pcolor(X,Y,sxx);
px.EdgeColor="none";
colorbar

Figure contains an axes object. The axes object contains an object of type surface.

Reshape the y-component of the normal stress to the shape of the grid and plot it.

syy = reshape(intrpStress.syy,size(Y));
figure
py = pcolor(X,Y,syy);
py.EdgeColor="none";
colorbar

Figure contains an axes object. The axes object contains an object of type surface.

Open Live Script

Analyze a bimetallic cable under tension, and interpolate stress on a cross-section of the cable.

Create and plot a bimetallic cable geometry.

gm = multicylinder([0.01,0.015],0.05);
pdegplot(gm,FaceLabels="on", ...
            CellLabels="on", ...
            FaceAlpha=0.5)

Figure contains an axes object. The axes object contains 6 objects of type quiver, text, patch, line.

Create an femodel object for static structural analysis and include the geometry into the model.

model = femodel(AnalysisType="structuralStatic", ...
                Geometry=gm);

Specify Young's modulus and Poisson's ratio for each metal.

model.MaterialProperties(1) = ...
    materialProperties(YoungsModulus=110E9, ...
                       PoissonsRatio=0.28);
model.MaterialProperties(2) = ...
    materialProperties(YoungsModulus=210E9, ...
                       PoissonsRatio=0.3);

Specify that faces 1 and 4 are fixed boundaries.

model.FaceBC([1 4]) = faceBC(Constraint="fixed");

Specify the surface traction for faces 2 and 5.

model.FaceLoad([2 5]) = faceLoad(SurfaceTraction=[0;0;100]);

Generate a mesh and solve the problem.

model = generateMesh(model);
R = solve(model)
R = 
  StaticStructuralResults with properties:

      Displacement: [1x1 FEStruct]
            Strain: [1x1 FEStruct]
            Stress: [1x1 FEStruct]
    VonMisesStress: [23098x1 double]
              Mesh: [1x1 FEMesh]

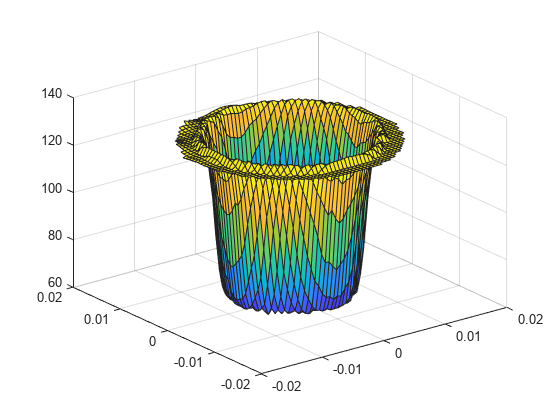
Define coordinates of a midspan cross-section of the cable.

[X,Y] = meshgrid(linspace(-0.015,0.015,50));
Z = ones(size(X))*0.025;

Interpolate the stress and plot the result.

intrpStress = interpolateStress(R,X,Y,Z);
surf(X,Y,reshape(intrpStress.szz,size(X)))

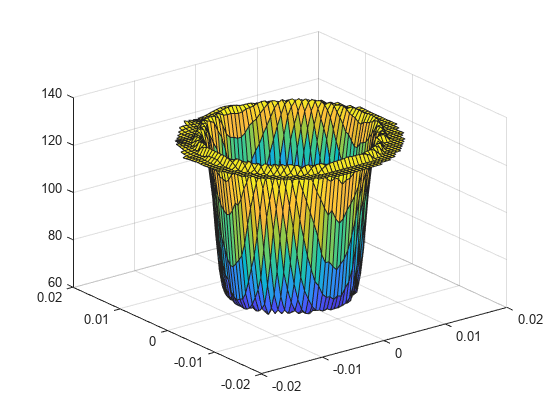
Figure contains an axes object. The axes object contains an object of type surface.

Alternatively, you can specify the grid by using a matrix of query points.

querypoints = [X(:),Y(:),Z(:)]';
intrpStress = interpolateStress(R,querypoints);
surf(X,Y,reshape(intrpStress.szz,size(X)))

Figure contains an axes object. The axes object contains an object of type surface.

Open Live Script

Interpolate the stress at the geometric center of a beam under a harmonic excitation.

Create and plot a beam geometry.

gm = multicuboid(0.06,0.005,0.01);
pdegplot(gm,FaceLabels="on",FaceAlpha=0.5)
view(50,20)

Figure contains an axes object. The axes object contains 6 objects of type quiver, text, patch, line.

Create an femodel object for transient structural analysis and include the geometry into the model.

model = femodel(AnalysisType="structuralTransient", ...
                Geometry=gm);

Specify Young's modulus, Poisson's ratio, and the mass density of the material.

model.MaterialProperties = ...
    materialProperties(YoungsModulus=210E9, ...
                       PoissonsRatio=0.3, ...
                       MassDensity=7800);

Fix one end of the beam.

model.FaceBC(5) = faceBC(Constraint="fixed");

Apply a sinusoidal displacement along the y-direction on the end opposite the fixed end of the beam.

yDisplacementFunc = ...
@(location,state) ones(size(location.y))*1E-4*sin(50*state.time);
model.FaceBC(3) = faceBC(YDisplacement=yDisplacementFunc);

Generate a mesh.

model = generateMesh(model,Hmax=0.01);

Specify the zero initial displacement and velocity.

model.CellIC = cellIC(Displacement=[0;0;0],Velocity=[0;0;0]);

Solve the problem.

tlist = 0:0.002:0.2;
R = solve(model,tlist);

Interpolate the stress at the geometric center of the beam.

coordsMidSpan = [0;0;0.005];
intrpStress = interpolateStress(R,coordsMidSpan);

Plot the normal stress at the geometric center of the beam.

figure
plot(R.SolutionTimes,intrpStress.sxx)
title("X-Direction Normal Stress at Beam Center")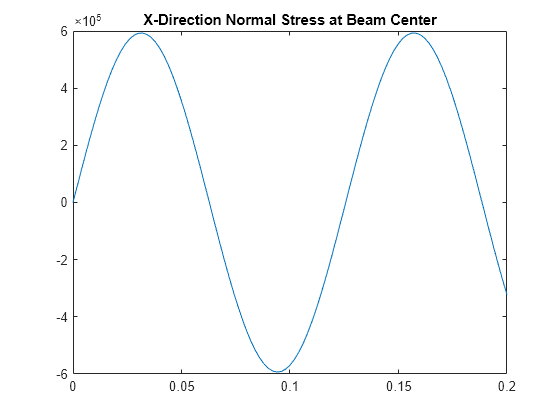

Figure contains an axes object. The axes object with title X-Direction Normal Stress at Beam Center contains an object of type line.

Input Arguments

collapse all

Solution of the structural analysis problem, specified as a StaticStructuralResults, TransientStructuralResults, or FrequencyStructuralResults object. Create structuralresults by using the solve function.

x-coordinate query points, specified as a real array. interpolateStress evaluates the stresses at the 2-D coordinate points [xq(i),yq(i)] or at the 3-D coordinate points [xq(i),yq(i),zq(i)]. Therefore, xq, yq, and (if present) zq must have the same number of entries.

interpolateStress converts the query points to column vectors xq(:), yq(:), and (if present) zq(:). It returns stresses as an FEStruct object with the properties containing vectors of the same size as these column vectors. To ensure that the dimensions of the returned solution are consistent with the dimensions of the original query points, use the reshape function. For example, use intrpStress = reshape(intrpStress.sxx,size(xq)).

Data Types: double

y-coordinate query points, specified as a real array. interpolateStress evaluates the stresses at the 2-D coordinate points [xq(i),yq(i)] or at the 3-D coordinate points [xq(i),yq(i),zq(i)]. Therefore, xq, yq, and (if present) zq must have the same number of entries. Internally, interpolateStress converts the query points to the column vector yq(:).

Data Types: double

z-coordinate query points, specified as a real array. interpolateStress evaluates the stresses at the 3-D coordinate points [xq(i),yq(i),zq(i)]. Therefore, xq, yq, and zq must have the same number of entries. Internally, interpolateStress converts the query points to the column vector zq(:).

Data Types: double

Query points, specified as a real matrix with either two rows for 2-D geometry or three rows for 3-D geometry. interpolateStress evaluates stresses at the coordinate points querypoints(:,i), so each column of querypoints contains exactly one 2-D or 3-D query point.

Example: For 2-D geometry, querypoints = [0.5,0.5,0.75,0.75; 1,2,0,0.5]

Data Types: double

Output Arguments

collapse all

Stresses at the query points, returned as an FEStruct object with the properties representing spatial components of stress at the query points. For query points that are outside the geometry, intrpStress returns NaN. Properties of an FEStruct object are read-only.

Version History

Introduced in R2017b

expand all

See Also

Objects

Functions