evaluateTemperatureGradient

Evaluate temperature gradient of thermal solution at arbitrary spatial locations

Syntax

[gradTx,gradTy]
= evaluateTemperatureGradient(thermalresults,xq,yq)

[gradTx,gradTy,gradTz]
= evaluateTemperatureGradient(thermalresults,xq,yq,zq)

[___] = evaluateTemperatureGradient(thermalresults,querypoints)

[___] = evaluateTemperatureGradient(___,iT)

Description

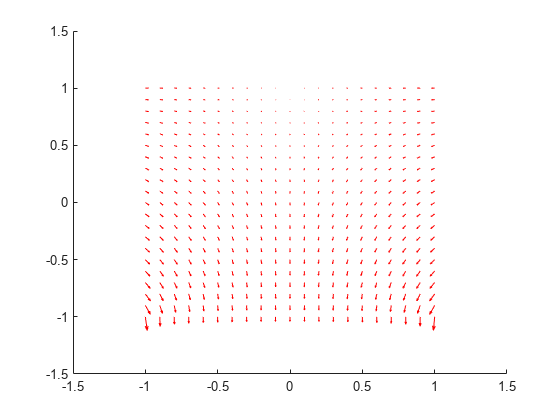
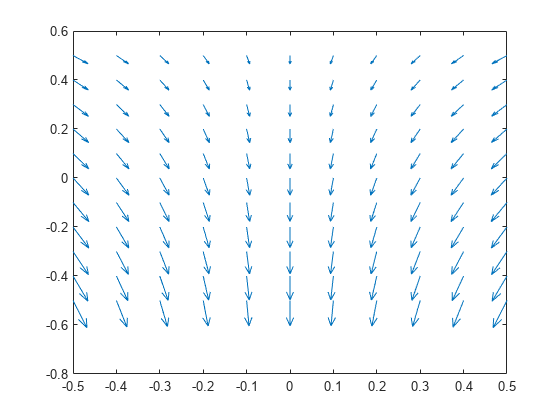
[gradTx,gradTy] = evaluateTemperatureGradient(thermalresults,xq,yq) returns the interpolated values of temperature gradients of the thermal model solution thermalresults at the 2-D points specified in xq and yq. This syntax is valid for both the steady-state and transient thermal models.

example

[gradTx,gradTy,gradTz] = evaluateTemperatureGradient(thermalresults,xq,yq,zq) returns the interpolated temperature gradients at the 3-D points specified in xq, yq, and zq. This syntax is valid for both the steady-state and transient thermal models.

example

[___] = evaluateTemperatureGradient(thermalresults,querypoints) returns the interpolated values of the temperature gradients at the points specified in querypoints. This syntax is valid for both the steady-state and transient thermal models.

example

[___] = evaluateTemperatureGradient(___,iT) returns the interpolated values of the temperature gradients for the time-dependent equation at times iT. Specify iT after the input arguments in any of the previous syntaxes.

The first dimension of gradTx, gradTy, and, in 3-D case, gradTz corresponds to query points. The second dimension corresponds to time-steps iT.

example

Examples

collapse all

Temperature Gradients for 2-D Steady-State Thermal Problem

Open Live Script

For a 2-D steady-state thermal problem, evaluate temperature gradients at the nodal locations and at the points specified by x and y coordinates.

Create and plot a square geometry.

R1 = [3,4,-1,1,1,-1,1,1,-1,-1]';
g = decsg(R1,'R1',('R1')');
pdegplot(g,EdgeLabels="on")
xlim([-1.1 1.1])
ylim([-1.1 1.1])

Figure contains an axes object. The axes object contains 5 objects of type line, text.

Create an femodel object for steady-state thermal analysis and include the geometry into the model.

model = femodel(AnalysisType="thermalSteady", ...
                Geometry=g);

Assuming that this geometry represents an iron plate, the thermal conductivity is $79.5 W / (m K)$ .

model.MaterialProperties = ...
    materialProperties(ThermalConductivity=79.5);

Apply a constant temperature of 300 K to the bottom of the plate (edge 3).

model.EdgeBC(3) = edgeBC(Temperature=300);

Apply convection on the two sides of the plate (edges 2 and 4).

model.EdgeLoad([2 4]) = ...
    edgeLoad(ConvectionCoefficient=25,...
             AmbientTemperature=50);

Mesh the geometry and solve the problem.

model = generateMesh(model);
R = solve(model)

R = 
  SteadyStateThermalResults with properties:

    Temperature: [1529x1 double]
     XGradients: [1529x1 double]
     YGradients: [1529x1 double]
     ZGradients: []
           Mesh: [1x1 FEMesh]

The solver finds the temperatures and temperature gradients at the nodal locations. To access these values, use R.Temperature, R.XGradients, and so on. For example, plot the temperature gradients at nodal locations.

figure
pdeplot(R.Mesh,FlowData=[R.XGradients R.YGradients]);

Figure contains an axes object. The axes object contains an object of type quiver.

Create a grid specified by x and y coordinates, and evaluate temperature gradients to the grid.

v = linspace(-0.5,0.5,11);
[X,Y] = meshgrid(v);

[gradTx,gradTy] = ...
evaluateTemperatureGradient(R,X,Y);

Reshape the gradTx and gradTy vectors, and plot the resulting temperature gradients.

gradTx = reshape(gradTx,size(X));
gradTy = reshape(gradTy,size(Y));
figure
quiver(X,Y,gradTx,gradTy)

Figure contains an axes object. The axes object contains an object of type quiver.

Alternatively, you can specify the grid by using a matrix of query points.

querypoints = [X(:) Y(:)]';
[gradTx,gradTy] = ...
evaluateTemperatureGradient(R,querypoints);

gradTx = reshape(gradTx,size(X));
gradTy = reshape(gradTy,size(Y));
figure
quiver(X,Y,gradTx,gradTy)

Figure contains an axes object. The axes object contains an object of type quiver.

Temperature Gradients for 3-D Steady-State Thermal Problem

Open Live Script

For a 3-D steady-state thermal problem, evaluate temperature gradients at the nodal locations and at the points specified by x, y, and z coordinates.

Create an femodel object for steady-state thermal analysis and include a block geometry into the model.

model = femodel(AnalysisType="thermalSteady", ...
                Geometry="Block.stl");

Plot the geometry.

pdegplot(model.Geometry,FaceLabels="on",FaceAlpha=0.5)
title("Copper block, cm")

Figure contains an axes object. The axes object with title Copper block, cm contains 6 objects of type quiver, text, patch, line.

Assuming that this is a copper block, the thermal conductivity of the block is approximately $4 W / (c m K)$ .

model.MaterialProperties = ...
    materialProperties(ThermalConductivity=4);

Apply a constant temperature of 373 K to the left side of the block (edge 1) and a constant temperature of 573 K to the right side of the block.

model.FaceBC(1) = faceBC(Temperature=373);
model.FaceBC(3) = faceBC(Temperature=573);

Apply a heat flux boundary condition to the bottom of the block.

model.FaceLoad(4) = faceLoad(Heat=-20);

Mesh the geometry and solve the problem.

model = generateMesh(model);
R = solve(model)

R = 
  SteadyStateThermalResults with properties:

    Temperature: [12822x1 double]
     XGradients: [12822x1 double]
     YGradients: [12822x1 double]
     ZGradients: [12822x1 double]
           Mesh: [1x1 FEMesh]

The solver finds the values of temperatures and temperature gradients at the nodal locations. To access these values, use R.Temperature, R.XGradients, and so on.

Create a grid specified by x, y, and z coordinates, and evaluate temperature gradients to the grid.

[X,Y,Z] = meshgrid(1:26:100,1:6:20,1:11:50);

[gradTx,gradTy,gradTz] = ...
evaluateTemperatureGradient(R,X,Y,Z);

Reshape the gradTx, gradTy, and gradTz vectors, and plot the resulting temperature gradients.

gradTx = reshape(gradTx,size(X));
gradTy = reshape(gradTy,size(Y));
gradTz = reshape(gradTz,size(Z));

figure
quiver3(X,Y,Z,gradTx,gradTy,gradTz)
axis equal
xlabel("x")
ylabel("y")
zlabel("z")

Figure contains an axes object. The axes object with xlabel x, ylabel y contains an object of type quiver.

Alternatively, you can specify the grid by using a matrix of query points.

querypoints = [X(:) Y(:) Z(:)]';
[gradTx,gradTy,gradTz] = ...
evaluateTemperatureGradient(R,querypoints);

gradTx = reshape(gradTx,size(X));
gradTy = reshape(gradTy,size(Y));
gradTz = reshape(gradTz,size(Z));

figure
quiver3(X,Y,Z,gradTx,gradTy,gradTz)
axis equal
xlabel("x")
ylabel("y")
zlabel("z")

Figure contains an axes object. The axes object with xlabel x, ylabel y contains an object of type quiver.

Temperature Gradients for Transient Thermal Problem on Square

Open Live Script

Solve a 2-D transient heat transfer problem on a square domain and compute temperature gradients at the convective boundary.

Create an femodel object for transient thermal analysis and include a square geometry into the model.

model = femodel(AnalysisType="thermalTransient", ...
                Geometry=@squareg);

Plot the geometry.

pdegplot(model.Geometry,EdgeLabels="on")
xlim([-1.1 1.1])
ylim([-1.1 1.1])

Figure contains an axes object. The axes object contains 5 objects of type line, text.

Assign the following thermal properties: thermal conductivity is $100 W / (m^{\circ} C)$ , mass density is $7800 k g / m^{3}$ , and specific heat is $500 J / (k g^{\circ} C)$ .

model.MaterialProperties = ...
    materialProperties(ThermalConductivity=100,...
                       MassDensity=7800,...
                       SpecificHeat=500);

Apply the convection boundary condition on the right edge.

model.EdgeLoad(2) = ...
    edgeLoad(ConvectionCoefficient=5000,...
             AmbientTemperature=25);

Set the initial conditions: uniform room temperature across domain and higher temperature on the left edge.

model.FaceIC = faceIC(Temperature=25);
model.EdgeIC(4) = edgeIC(Temperature=100);

Generate a mesh and solve the problem using 0:1000:200000 as a vector of times.

model = generateMesh(model);
tlist = 0:1000:200000;
R = solve(model,tlist);

Define a line at convection boundary and compute temperature gradients across that line.

X = -1:0.1:1;
Y = ones(size(X));

[gradTx,gradTy] = ...
    evaluateTemperatureGradient(R,X,Y,1:length(tlist));

Plot the interpolated gradient component gradTx along the x axis for the following values from the time interval tlist.

figure
t = [51:50:201];
for i = t
  p(i) = plot(X,gradTx(:,i), ...
      DisplayName=strcat("t=",num2str(tlist(i))));
  hold on
end
legend(p(t))
xlabel("x")
ylabel("gradTx")

Figure contains an axes object. The axes object with xlabel x, ylabel gradTx contains 4 objects of type line. These objects represent t=50000, t=100000, t=150000, t=200000.

Input Arguments

collapse all

`thermalresults` — Solution of thermal problem
`SteadyStateThermalResults` object | `TransientThermalResults` object

Solution of a thermal problem, specified as a SteadyStateThermalResults object or a TransientThermalResults object. Create thermalresults using the solve function.

`xq` — x-coordinate query points
real array

x-coordinate query points, specified as a real array. evaluateTemperatureGradient evaluates temperature gradient at the 2-D coordinate points [xq(i) yq(i)] or at the 3-D coordinate points [xq(i) yq(i) zq(i)]. So xq, yq, and (if present) zq must have the same number of entries.

evaluateTemperatureGradient converts query points to column vectors xq(:), yq(:), and (if present) zq(:). It returns the temperature gradient in a form of a column vector of the same size. To ensure that the dimensions of the returned solution is consistent with the dimensions of the original query points, use reshape. For example, use gradTx = reshape(gradTx,size(xq)).

Data Types: double

`yq` — y-coordinate query points
real array

y-coordinate query points, specified as a real array. evaluateTemperatureGradient evaluates the temperature gradient at the 2-D coordinate points [xq(i) yq(i)] or at the 3-D coordinate points [xq(i) yq(i) zq(i)]. So xq, yq, and (if present) zq must have the same number of entries.

Data Types: double

`zq` — z-coordinate query points
real array

z-coordinate query points, specified as a real array. evaluateTemperatureGradient evaluates the temperature gradient at the 3-D coordinate points [xq(i) yq(i) zq(i)]. So xq, yq, and zq must have the same number of entries.

Data Types: double

`querypoints` — Query points
real matrix

Query points, specified as a real matrix with either two rows for 2-D geometry, or three rows for 3-D geometry. evaluateTemperatureGradient evaluates the temperature gradient at the coordinate points querypoints(:,i), so each column of querypoints contains exactly one 2-D or 3-D query point.

Example: For 2-D geometry, querypoints = [0.5 0.5 0.75 0.75; 1 2 0 0.5]

Data Types: double

`iT` — Time indices
vector of positive integers

Time indices, specified as a vector of positive integers. Each entry in iT specifies a time index.

Example: iT = 1:5:21 specifies every fifth time-step up to 21.

Data Types: double

Output Arguments

collapse all

`gradTx` — x-component of the temperature gradient
matrix

x-component of the temperature gradient, returned as a matrix. For query points that are outside the geometry, gradTx = NaN.

`gradTy` — y-component of the temperature gradient
matrix

y-component of the temperature gradient, returned as a matrix. For query points that are outside the geometry, gradTy = NaN.

`gradTz` — z-component of the temperature gradient
matrix

z-component of the temperature gradient, returned as a matrix. For query points that are outside the geometry, gradTz = NaN.

Version History

Introduced in R2017a

evaluateTemperatureGradient

Syntax

Description

Examples

Temperature Gradients for 2-D Steady-State Thermal Problem

Temperature Gradients for 3-D Steady-State Thermal Problem

Temperature Gradients for Transient Thermal Problem on Square

Input Arguments

`thermalresults` — Solution of thermal problem
`SteadyStateThermalResults` object | `TransientThermalResults` object

`xq` — x-coordinate query points
real array

`yq` — y-coordinate query points
real array

`zq` — z-coordinate query points
real array

`querypoints` — Query points
real matrix

`iT` — Time indices
vector of positive integers

Output Arguments

`gradTx` — x-component of the temperature gradient
matrix

`gradTy` — y-component of the temperature gradient
matrix

`gradTz` — z-component of the temperature gradient
matrix

Version History

See Also

Objects

Functions

evaluateTemperatureGradient

Syntax

Description

Examples

Temperature Gradients for 2-D Steady-State Thermal Problem

Temperature Gradients for 3-D Steady-State Thermal Problem

Temperature Gradients for Transient Thermal Problem on Square

Input Arguments

thermalresults — Solution of thermal problem SteadyStateThermalResults object | TransientThermalResults object

xq — x-coordinate query points real array

yq — y-coordinate query points real array

zq — z-coordinate query points real array

querypoints — Query points real matrix

iT — Time indices vector of positive integers

Output Arguments

gradTx — x-component of the temperature gradient matrix

gradTy — y-component of the temperature gradient matrix

gradTz — z-component of the temperature gradient matrix

Version History

See Also

Objects

Functions

`thermalresults` — Solution of thermal problem
`SteadyStateThermalResults` object | `TransientThermalResults` object

`xq` — x-coordinate query points
real array

`yq` — y-coordinate query points
real array

`zq` — z-coordinate query points
real array

`querypoints` — Query points
real matrix

`iT` — Time indices
vector of positive integers

`gradTx` — x-component of the temperature gradient
matrix

`gradTy` — y-component of the temperature gradient
matrix

`gradTz` — z-component of the temperature gradient
matrix