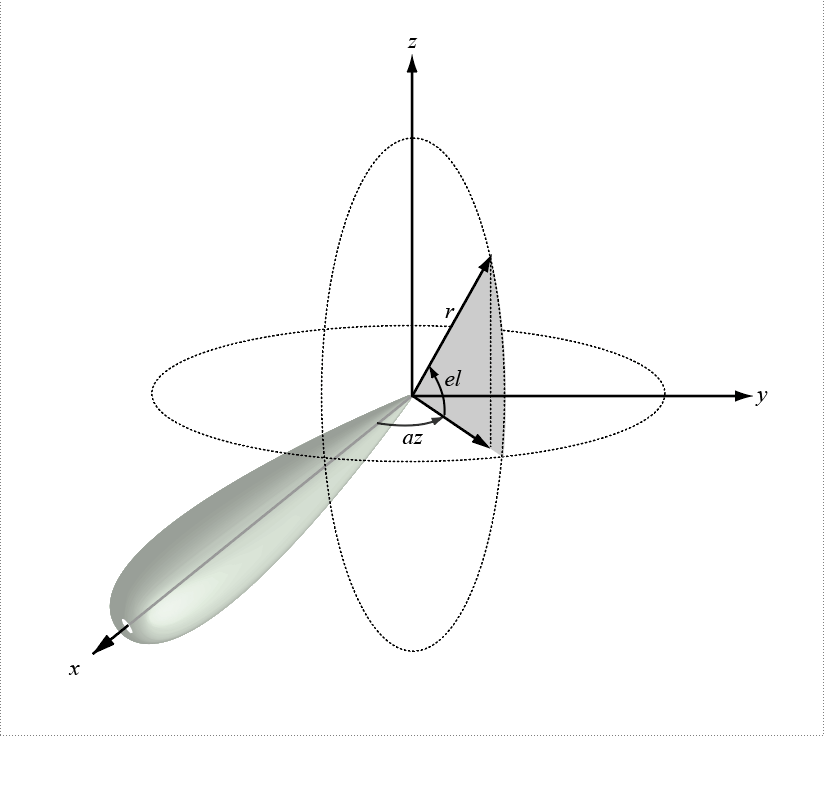
global2localcoord
Convert global to local coordinates
Syntax
Description
lclCoord = global2localcoord(___,localOrigin)localOrigin. Use this syntax with any of the input arguments in
previous syntaxes.
Examples
Input Arguments
Output Arguments
More About
References
[1] Foley, J. D., A. van Dam, S. K. Feiner, and J. F. Hughes. Computer Graphics: Principles and Practice in C, 2nd Ed. Reading, MA: Addison-Wesley, 1995.
Extended Capabilities
Version History
Introduced in R2011a
See Also
local2globalcoord | uv2azel | phitheta2azel | azel2uv | azel2phitheta | rangeangle