trendability
Measure of similarity between trajectories of condition indicators
Syntax
Description
Y = trendability(X)X. Use
trendability as measure of similarity between the trajectories of a
feature measured in several run-to-failure experiments. A more trendable feature has
trajectories with the same underlying shape. The values of Y range from
0 to 1, where Y is 1 if X is perfectly trendable
and 0 if X is non-trendable.
Y = trendability(X,lifetimeVar)X using the lifetime
variable lifetimeVar.
Y = trendability(X,lifetimeVar,dataVar)X using the data
variables specified by dataVar.
Y = trendability(X,lifetimeVar,dataVar,memberVar)X using the lifetime
variable lifetimeVar, the data variables specified by
dataVar, and the member variable
memberVar.
Y = trendability(___,Name,Value)Name,Value pair arguments. You can use this syntax with any of the
previous input-argument combinations.
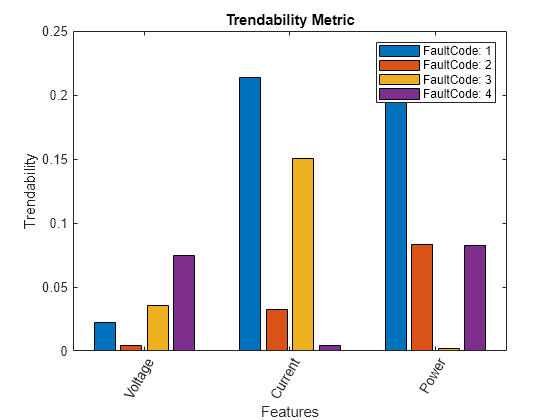
trendability(___) with no output arguments plots a
bar chart of ranked trendability values.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Limitations
When
Xis a tall table or tall timetable,trendabilitynevertheless loads the complete array into memory usinggather. If the memory available is inadequate, thentrendabilityreturns an error.
Algorithms
The computation of trendability uses this formula:
where xj represents the vector of measurements of a feature on the jth system and the variable M is the number of systems monitored.
When xj and xk have different lengths, the shorter vector is resampled to match the length of the longer vector. To facilitate this process, their time vectors are first normalized to percent lifetime, that is, [0%, 100%].
References
[1] Coble, J., and J. W. Hines. "Identifying Optimal Prognostic Parameters from Data: A Genetic Algorithms Approach." In Proceedings of the Annual Conference of the Prognostics and Health Management Society. 2009.
[2] Coble, J. "Merging Data Sources to Predict Remaining Useful Life - An Automated Method to Identify Prognostics Parameters." Ph.D. Thesis. University of Tennessee, Knoxville, TN, 2010.
[3] Lei, Y. Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery. Xi'an, China: Xi'an Jiaotong University Press, 2017.
[4] Lofti, S., J. B. Ali, E. Bechhoefer, and M. Benbouzid. "Wind turbine high-speed shaft bearings health prognosis through a spectral Kurtosis-derived indices and SVR." Applied Acoustics Vol. 120, 2017, pp. 1-8.
Version History
Introduced in R2018b