rlValueFunction
Description
This object implements a value function approximator object that you can use as a
critic for a reinforcement learning agent. A value function (also known as state-value
function) is a mapping from an environment observation to the value of a policy. Specifically,
its output is a scalar that represents the expected discounted cumulative long-term reward
when an agent starts from the state corresponding to the given observation and executes
actions according to a given policy afterwards. After you create an
rlValueFunction critic, use it to create an agent such as an rlACAgent, rlPGAgent, or rlPPOAgent agent. For
an example of this workflow, see Create Actor and Critic Representations. For more information on creating
actors and critics, see Create Policies and Value Functions.
Creation
Syntax
Description
critic = rlValueFunction(net,observationInfo)critic using the deep neural
network net as approximation model, and sets the
ObservationInfo property of critic to the
observationInfo input argument. The network input layers are
automatically associated with the environment observation channels according to the
dimension specifications in observationInfo.
critic = rlValueFunction(tab,observationInfo)critic with a discrete
observation space, from the table tab, which is an
rlTable object
containing a column array with as many elements as the number of possible observations.
The function sets the ObservationInfo property of
critic to the observationInfo input
argument, which in this case must be a scalar rlFiniteSetSpec
object.
critic = rlValueFunction({basisFcn,W0},observationInfo)critic using a custom basis
function as underlying approximator. The first input argument is a two-element cell
array whose first element is the handle basisFcn to a custom basis
function and whose second element is the initial weight vector W0.
The function sets the ObservationInfo property of
critic to the observationInfo input
argument.
critic = rlValueFunction(___,Name=Value)UseDevice property using one or more name-value arguments.
Specifying the input layer names allows you explicitly associate the layers of your
network approximator with specific environment channels. For all types of approximators,
you can specify the device where computations for critic are
executed, for example UseDevice="gpu".
Input Arguments
Deep neural network used as the underlying approximator within the critic, specified as one of the following:
Array of
LayerobjectslayerGraphobjectDAGNetworkobjectSeriesNetworkobjectdlnetworkobject
Note
Among the different network representation options, dlnetwork is preferred, since it
has built-in validation checks and supports automatic differentiation. If you pass
another network object as an input argument, it is internally converted to a
dlnetwork object. However, best practice is to convert other
representations to dlnetwork explicitly before
using them to create a critic or an actor for a reinforcement learning agent. You can
do so using dlnet=dlnetwork(net), where net is
any Deep Learning Toolbox™ neural network object. The resulting dlnet is the
dlnetwork object that you use for your critic or actor. This
practice allows a greater level of insight and control for cases in which the
conversion is not straightforward and might require additional
specifications.
The network must have as many input layers as the number of environment observation channels (with each input layer receiving input from an observation channel), and a single output layer returning a scalar value.
rlValueFunction objects support recurrent deep neural
networks.
The learnable parameters of the critic are the weights of the deep neural network. For a list of deep neural network layers, see List of Deep Learning Layers. For more information on creating deep neural networks for reinforcement learning, see Create Policies and Value Functions.
Value table, specified as an rlTable object
containing a column vector with length equal to the number of possible observations
from the environment. Each element is the predicted discounted cumulative long-term
reward when the agent starts from the given observation and takes the best possible
action. The elements of this vector are the learnable parameters of the
representation.
Custom basis function, specified as a function handle to a user-defined function.
The user defined function can either be an anonymous function or a function on the
MATLAB path. The output of the critic is the scalar c = W'*B, where
W is a weight vector containing the learnable parameters and
B is the column vector returned by the custom basis
function.
Your basis function must have the following signature.
B = myBasisFunction(obs1,obs2,...,obsN)
Here, obs1 to obsN are inputs in the same
order and with the same data type and dimensions as the environment observation
channels defined in observationInfo.
For an example on how to use a basis function to create a value function critic with a mixed continuous and discrete observation space, see Create Hybrid Observation Space Value Function Critic from Custom Basis Function.
Example: @(obs1,obs2,obs3) [obs3(1)*obs1(1)^2;
abs(obs2(5)+obs1(2))]
Initial value of the basis function weights W, specified as a
column vector having the same length as the vector returned by the basis
function.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: UseDevice="gpu"
Network input layers names corresponding to the environment observation channels,
specified as a string array or a cell array of strings or character vectors. The
function assigns, in sequential order, each environment observation channel specified in
observationInfo to each layer whose name is specified in the
array assigned to this argument. Therefore, the specified network input layers, ordered
as indicated in this argument, must have the same data type and dimensions as the
observation channels, as ordered in observationInfo.
This name-value argument is supported only when the approximation model is a deep neural network.
Example: ObservationInputNames={"obsInLyr1_airspeed","obsInLyr2_altitude"}
Properties
Observation specifications, specified as an rlFiniteSetSpec
or rlNumericSpec
object or an array containing a mix of such objects. Each element in the array defines
the properties of an environment observation channel, such as its dimensions, data type,
and name.
When you create the approximator object, the constructor function sets the
ObservationInfo property to the input argument
observationInfo.
You can extract observationInfo from an existing environment,
function approximator, or agent using getObservationInfo. You can also construct the specifications manually
using rlFiniteSetSpec
or rlNumericSpec.
Example: [rlNumericSpec([2 1])
rlFiniteSetSpec([3,5,7])]
Normalization method, returned as an array in which each element (one for each input
channel defined in the observationInfo and
actionInfo properties, in that order) is one of the following
values:
"none"— Do not normalize the input."rescale-zero-one"— Normalize the input by rescaling it to the interval between 0 and 1. The normalized input Y is (U–Min)./(UpperLimit–LowerLimit), where U is the nonnormalized input. Note that nonnormalized input values lower thanLowerLimitresult in normalized values lower than 0. Similarly, nonnormalized input values higher thanUpperLimitresult in normalized values higher than 1. Here,UpperLimitandLowerLimitare the corresponding properties defined in the specification object of the input channel."rescale-symmetric"— Normalize the input by rescaling it to the interval between –1 and 1. The normalized input Y is 2(U–LowerLimit)./(UpperLimit–LowerLimit) – 1, where U is the nonnormalized input. Note that nonnormalized input values lower thanLowerLimitresult in normalized values lower than –1. Similarly, nonnormalized input values higher thanUpperLimitresult in normalized values higher than 1. Here,UpperLimitandLowerLimitare the corresponding properties defined in the specification object of the input channel.
Note
When you specify the Normalization property of
rlAgentInitializationOptions, normalization is applied only to
the approximator input channels corresponding to rlNumericSpec specification objects in which both the
UpperLimit and LowerLimit properties
are defined. After you create the agent, you can use setNormalizer to assign normalizers that use any normalization
method. For more information on normalizer objects, see rlNormalizer.
Example: "rescale-symmetric"
Computation device used to perform operations such as gradient computation, parameter
update and prediction during training and simulation, specified as either
"cpu" or "gpu".
The "gpu" option requires both Parallel Computing Toolbox™ software and a CUDA® enabled NVIDIA® GPU. For more information on supported GPUs see GPU Computing Requirements (Parallel Computing Toolbox).
You can use gpuDevice (Parallel Computing Toolbox) to query or select a local GPU device to be
used with MATLAB®.
Note
Training or simulating an agent on a GPU involves device-specific numerical round-off errors. Because of these errors, you can get different results on a GPU and on a CPU for the same operation.
To speed up training by using parallel processing over multiple cores, you do not need
to use this argument. Instead, when training your agent, use an rlTrainingOptions object in which the UseParallel
option is set to true. For more information about training using
multicore processors and GPUs for training, see Train Agents Using Parallel Computing and GPUs.
Example: "gpu"
Learnable parameters of the approximator object, specified as a cell array of
dlarray objects. This property contains the learnable parameters of
the approximation model used by the approximator object.
Example: {dlarray(rand(256,4)),dlarray(rand(256,1))}
State of the approximator object, specified as a cell array of
dlarray objects. For dlnetwork-based models, this
property contains the Value column of the
State property table of the dlnetwork model.
The elements of the cell array are the state of the recurrent neural network used in the
approximator (if any), as well as the state for the batch normalization layer (if
used).
For model types that are not based on a dlnetwork object, this
property is an empty cell array, since these model types do not support states.
Example: {dlarray(rand(256,1)),dlarray(rand(256,1))}
Object Functions
rlACAgent | Actor-critic (AC) reinforcement learning agent |
rlPGAgent | Policy gradient (PG) reinforcement learning agent |
rlPPOAgent | Proximal policy optimization (PPO) reinforcement learning agent |
getValue | Obtain estimated value from a critic given environment observations and actions |
evaluate | Evaluate function approximator object given observation (or observation-action) input data |
getLearnableParameters | Obtain learnable parameter values from agent, function approximator, or policy object |
setLearnableParameters | Set learnable parameter values of agent, function approximator, or policy object |
setModel | Set approximation model in function approximator object |
getModel | Get approximation model from function approximator object |
Examples
Create an observation specification object (or alternatively use getObservationInfo to extract the specification object from an environment). For this example, define the observation space as a continuous four-dimensional space, so that there is a single observation channel that carries a column vector containing four doubles.
obsInfo = rlNumericSpec([4 1]);
A value-function critic takes the current observation as input and returns a single scalar as output (the estimated discounted cumulative long-term reward for following the policy from the state corresponding to the current observation).
To model the parametrized value function within the critic, use a neural network with one input layer (which returns the content of the observation channel, as specified by obsInfo) and one output layer (returning the scalar value). Note that prod(obsInfo.Dimension) returns the total number of dimensions of the observation space regardless of whether the observation space is a column vector, row vector, or matrix.
Define the network as an array of layer objects.
net = [
featureInputLayer(prod(obsInfo.Dimension));
fullyConnectedLayer(10);
reluLayer;
fullyConnectedLayer(1)
];Convert the network to a dlnetwork object.
dlnet = dlnetwork(net);
You can plot the network using plot and display its main characteristics, like the number of weights, using summary.
plot(dlnet)
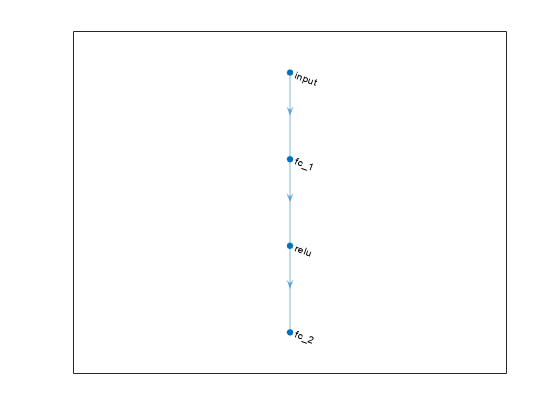
summary(dlnet)
Initialized: true
Number of learnables: 61
Inputs:
1 'input' 4 features
Create the critic using the network and the observation specification object.
critic = rlValueFunction(dlnet,obsInfo)
critic =
rlValueFunction with properties:
ObservationInfo: [1×1 rl.util.rlNumericSpec]
Normalization: "none"
UseDevice: "cpu"
Learnables: {4×1 cell}
State: {0×1 cell}
To check your critic, use getValue to return the value of a random observation, using the current network weights.
v = getValue(critic,{rand(obsInfo.Dimension)})v = single
0.5196
You can now use the critic (along with an actor) to create an agent for the environment described by the given observation specification object. Examples of agents that can work with a continuous observation space, and use a value function critic, are rlACAgent, rlPGAgent, rlPPOAgent, and rlTRPOAgent.
For more information on creating approximator objects such as actors and critics, see Create Policies and Value Functions.
Create an actor and a critic that you can use to define a reinforcement learning agent such as an Actor-Critic (AC) agent. For this example, create actor and critic for an agent that can be trained against the cart-pole environment described in Train AC Agent to Balance Discrete Cart-Pole System.
First, create the environment. Then, extract the observation and action specifications from the environment. You need these specifications to define the agent and critic.
env = rlPredefinedEnv("CartPole-Discrete");
obsInfo = getObservationInfo(env);
actInfo = getActionInfo(env);A value-function critic takes the current observation as input and returns a single scalar as output (the estimated discounted cumulative long-term reward for following the policy from the state corresponding to the current observation).
To model the parametrized value function within the critic, use a neural network with one input layer (receiving the content of the observation channel, as specified by obsInfo) and one output layer (returning the scalar value).
Define the network as an array of layer objects, and get the dimension of the observation space from the environment specification objects. Name the network input layer criticNetInput.
CriticNet = [
featureInputLayer(prod(obsInfo.Dimension));
fullyConnectedLayer(10);
reluLayer;
fullyConnectedLayer(10);
reluLayer;
fullyConnectedLayer(1)];Convert the network to a dlnetwork object.
CriticNet = dlnetwork(CriticNet);
To display the network main characteristics, use summary.
summary(CriticNet)
Initialized: true
Number of learnables: 171
Inputs:
1 'input' 4 features
Create the critic using CriticNet and the environment specification object. Set the observation name to observation, which is the name of the criticNetwork input layer.
critic = rlValueFunction(CriticNet,obsInfo)
critic =
rlValueFunction with properties:
ObservationInfo: [1×1 rl.util.rlNumericSpec]
Normalization: "none"
UseDevice: "cpu"
Learnables: {6×1 cell}
State: {0×1 cell}
Check your critic using getValue to return the value of a random observation, given the current network weights.
v = getValue(critic,{rand(obsInfo.Dimension)})v = single
-0.3229
AC agents use a parametrized stochastic policy, which for discrete action spaces is implemented by a discrete categorical actor.
This actor takes an observation as input and returns as output a random action sampled (among the finite number of possible actions) from a categorical probability distribution.
To model the parametrized policy within the actor, use a neural network with one input layer (which receives the content of the environment observation channel, as specified by obsInfo) and one output layer. The output layer must return a vector of probabilities for each possible action, as specified by actInfo.
You can obtain the number of actions from the actInfo specification. Name the network output actorNetOutput.
actorNet = [
featureInputLayer(prod(obsInfo.Dimension))
fullyConnectedLayer(10);
reluLayer;
fullyConnectedLayer(10);
reluLayer;
fullyConnectedLayer(numel(actInfo.Elements)) ];Convert the network to a dlnetwork object.
actorNet = dlnetwork(actorNet);
To display the network main characteristics, use summary.
summary(actorNet)
Initialized: true
Number of learnables: 182
Inputs:
1 'input' 4 features
Create the actor using rlDiscreteCategoricalActor together with the observation and action specifications.
actor = rlDiscreteCategoricalActor(actorNet,obsInfo,actInfo)
actor =
rlDiscreteCategoricalActor with properties:
ObservationInfo: [1×1 rl.util.rlNumericSpec]
ActionInfo: [1×1 rl.util.rlFiniteSetSpec]
Normalization: "none"
UseDevice: "cpu"
Learnables: {6×1 cell}
State: {0×1 cell}
To check your actor, use getAction to return a random action from a given observation, using the current network weights.
a = getAction(actor,{rand(obsInfo.Dimension)})a = 1×1 cell array
{[-10]}
To return the probability distribution of the possible actions as a function of a random observation and given the current network weights, use evaluate.
prb = evaluate(actor,{rand(obsInfo.Dimension)})prb = 1×1 cell array
{2×1 single}
prb{1}ans = 2×1 single column vector
0.5917
0.4083
Specify the optimization options for the actor and the critic using rlOptimizerOptions. These options control the learning of the network parameters. For both networks, set the gradient threshold to 1. For this example, set the learning rate to 0.01. For the actor network, set the learning rate to 0.05.
criticOpts = rlOptimizerOptions( ... LearnRate=1e-2,... GradientThreshold=1); actorOpts = rlOptimizerOptions( ... LearnRate=5e-2,... GradientThreshold=1);
Specify agent options, including the objects previously created for both actor and critic.
agentOpts = rlACAgentOptions(... NumStepsToLookAhead=32,... DiscountFactor=0.99,... CriticOptimizerOptions=criticOpts,... ActorOptimizerOptions=actorOpts);
Create an AC agent using the actor, the critic and the agent options object.
agent = rlACAgent(actor,critic,agentOpts)
agent =
rlACAgent with properties:
AgentOptions: [1×1 rl.option.rlACAgentOptions]
UseExplorationPolicy: 1
ObservationInfo: [1×1 rl.util.rlNumericSpec]
ActionInfo: [1×1 rl.util.rlFiniteSetSpec]
SampleTime: 1
To check your agent, use getAction to return a random action from a given observation, using the current actor and critic network weights.
act = getAction(agent,{rand(obsInfo.Dimension)})act = 1×1 cell array
{[-10]}
For more information on creating approximator objects such as actors and critics, see Create Policies and Value Functions.
For additional examples showing how to create actors and critics for different agent types, see Compare DDPG Agent to LQR Controller and Train DQN Agent to Balance Discrete Cart-Pole System.
Create a finite set observation specification object (or alternatively use getObservationInfo to extract the specification object from an environment with a discrete observation space). For this example, define the observation space as a finite set consisting of four possible values 1, 3, 5 and 7.
obsInfo = rlFiniteSetSpec([1 3 5 7]);
A value-function critic takes the current observation as input and returns a single scalar value as output (the estimated discounted cumulative long-term reward for following the policy from the state corresponding to the current observation).
Since both observation and action spaces are discrete and low-dimensional, use a table to model the value function within the critic. rlTable creates a value table object from the observation and action specifications objects.
vTable = rlTable(obsInfo);
The table is a column vector in which each entry stores the value of the corresponding observation, under the given policy. You can access the table using the Table property of the vTable object. The initial value of each element is zero.
vTable.Table
ans = 4×1
0
0
0
0
You can also initialize the table to any value, in this case, an array containing all the integers from 1 to 4.
vTable.Table = reshape(1:4,4,1)
vTable =
rlTable with properties:
Table: [4×1 double]
Create the critic using the table and the observation specification object.
critic = rlValueFunction(vTable,obsInfo)
critic =
rlValueFunction with properties:
ObservationInfo: [1×1 rl.util.rlFiniteSetSpec]
Normalization: "none"
UseDevice: "cpu"
Learnables: {[4×1 dlarray]}
State: {}
To check your critic, use getValue to return the value of a given observation, using the current table entries.
v = getValue(critic,{7})v = 4
Obtain values for a random batch of 8 observations.
v = getValue(critic,{[1 3 5 7 7 5 3 1]})v = 1×8
1 2 3 4 4 3 2 1
Get the seventh value in the batch.
v(7)
ans = 2
You can now use the critic (along with an actor) to create an agent for the environment described by the given observation specification object. Examples of agents that can work with discrete observation spaces, and use a value function critic, are rlACAgent, rlPGAgent, rlPPOAgent. rlTRPOAgent does not support actors or critics that use tables.
For more information on creating approximator objects such as actors and critics, see Create Policies and Value Functions.
Create an observation specification object (or alternatively use getObservationInfo to extract the specification object from an environment). For this example, define the observation space as a continuous four-dimensional space, so that there is a single observation channel that carries a column vector containing four doubles.
obsInfo = rlNumericSpec([4 1]);
A value-function critic takes a batch of observations as input and returns a corresponding batch of scalars as output (each element in the batch is the estimated discounted cumulative long-term reward for following the policy from the state corresponding to the observation).
To model the parametrized value function within the critic, use a custom basis function. Create a custom function that returns a vector of three elements, given an observation as input. Here, the third dimension is the batch dimension. For each element of the batch dimension, the output of the basis function is a vector of three elements.
myBasisFcn = @(myobs) [
myobs(2,1,:).^2;
myobs(3,1,:)+myobs(1,1,:);
abs(myobs(4,1,:))
]myBasisFcn = function_handle with value:
@(myobs)[myobs(2,1,:).^2;myobs(3,1,:)+myobs(1,1,:);abs(myobs(4,1,:))]
The output of the critic is the scalar W'*myBasisFcn(myobs), which represents the estimated value of the observation under the given policy. Here W is a weight column vector which must have the same size as the custom basis function output. The elements of W are the learnable parameters.
Define an initial parameter vector.
W0 = [3;5;2];
Create the critic. The first argument is a two-element cell containing both the handle to the custom function and the initial weight vector. The second argument is the observation specification object.
critic = rlValueFunction({myBasisFcn,W0},obsInfo)critic =
rlValueFunction with properties:
ObservationInfo: [1×1 rl.util.rlNumericSpec]
Normalization: "none"
UseDevice: "cpu"
Learnables: {[1×3 dlarray]}
State: {}
To check your critic, use getValue to return the value of a given observation, using the current parameter vector.
v = getValue(critic,{[2 4 6 8]'})v = 104
Obtain values for a random batch of 10 observations.
v = getValue(critic,{rand(4,1,10)});Get the seventh value in the batch.
v(7)
ans = 6.9592
You can now use the critic (along with an actor) to create an agent for the environment described by the given observation specification object. Examples of agents that can work with continuous observation spaces, and use a value function critic, are rlACAgent, rlPGAgent, rlPPOAgent. rlTRPOAgent does not support actors or critics that use custom basis functions.
For more information on creating approximator objects such as actors and critics, see Create Policies and Value Functions.
Create an environment and obtain observation and action information.
env = rlPredefinedEnv("CartPole-Discrete");
obsInfo = getObservationInfo(env);A value-function critic takes the current observation as input and returns a single scalar value as output (the estimated discounted cumulative long-term reward for following the policy from the state corresponding to the current observation).
To model the parametrized value function within the critic, use a recurrent neural network with one input layer (receiving the content of the observation channel, as specified by obsInfo) and one output layer (returning the scalar value).
Define the network as an array of layer objects. To create a recurrent network, use a sequenceInputLayer as the input layer (with size equal to the number of dimensions of the observation channel) and include at least one lstmLayer.
myNet = [
sequenceInputLayer(obsInfo.Dimension(1))
fullyConnectedLayer(8)
reluLayer
lstmLayer(8)
fullyConnectedLayer(1)
];Convert the network to a dlnetwork object.
dlNet = dlnetwork(myNet);
Display a summary of network characteristics.
summary(dlNet)
Initialized: true
Number of learnables: 593
Inputs:
1 'sequenceinput' Sequence input with 4 dimensions
Create a value function representation object for the critic.
critic = rlValueFunction(dlNet,obsInfo)
critic =
rlValueFunction with properties:
ObservationInfo: [1×1 rl.util.rlNumericSpec]
Normalization: "none"
UseDevice: "cpu"
Learnables: {7×1 cell}
State: {2×1 cell}
To check your critic, use getValue to return the value of a random observation, using the current network weights.
v = getValue(critic,{rand(obsInfo.Dimension)})v = single
0.0017
You can use dot notation to extract and set the current state of the recurrent neural network in the critic.
critic.State
ans=2×1 cell array
{8×1 dlarray}
{8×1 dlarray}
critic.State = {
-0.1*dlarray(rand(8,1))
0.1*dlarray(rand(8,1))
};To evaluate the critic using sequential observations, use the sequence length (time) dimension. For example, obtain actions for 5 independent sequences each one consisting of 9 sequential observations.
[value,state] = getValue(critic, ...
{rand([obsInfo.Dimension 5 9])});Display the value corresponding to the seventh element of the observation sequence in the fourth sequence.
value(1,4,7)
ans = single
0.0769
Display the updated state of the recurrent neural network.
state
state=2×1 cell array
{8×5 single}
{8×5 single}
You can now use the critic (along with an actor) to create an agent for the environment described by the given observation specification object. Examples of agents that can work with continuous observation spaces, and use a value function critic, are rlACAgent, rlPGAgent, rlPPOAgent. rlTRPOAgent does not support actors or critics that use recurrent networks.
For more information on input and output format for recurrent neural networks, see the Algorithms section of lstmLayer. For more information on creating approximator objects such as critics and critics, see Create Policies and Value Functions.
Create a finite-set observation specification object (or alternatively use getObservationInfo to extract the specification object from an environment). For this example, define the observation space as an hybrid (that is mixed discrete-continuous) space with the discrete channel carrying a single observation labeled 7, 5, 3, or 1, and the second one being a vector over a continuous three-dimensional space.
obsInfo = [rlFiniteSetSpec([7 5 3 1]) rlNumericSpec([3 1])];
A value-function critic takes a batch of observations as input and returns as output a corresponding batch of scalars, each representing the estimated discounted cumulative long-term reward (the value) obtained by following the policy from the state corresponding to the given observation.
To model the parametrized value function within the critic, use a custom basis function. Create a custom function that returns a vector of four elements, given the content of the two observation channels as input. Note that the first channel carries a scalar (one row and one column) but the respective myBasisFcn input has also the batch dimension. Similarly, the second channel carries a vector with three elements, but it has the same batch dimension as the first channel. The sequence dimension is not supported for stateless approximators.
myBasisFcn = @(obsDisc,obsCont) [
obsDisc(1,1,:) + obsCont(1,1,:);
obsDisc(1,1,:) - obsCont(2,1,:);
obsDisc(1,1,:).^2 + obsCont(3,1,:);
obsDisc(1,1,:).^2 - obsCont(3,1,:)
];The output of the critic is the scalar W'*myBasisFcn(observation), which represents the estimated value of the observation under the given policy. Here W is a weight column vector which must have the same size as the custom basis function output. The elements of W are the learnable parameters.
Define an initial parameter vector.
W0 = ones(4,1);
Create the critic. The first argument is a two-element cell containing both the handle to the custom function and the initial weight vector. The second argument is the observation specification object.
critic = rlValueFunction({myBasisFcn,W0},obsInfo)critic =
rlValueFunction with properties:
ObservationInfo: [2×1 rl.util.RLDataSpec]
Normalization: ["none" "none"]
UseDevice: "cpu"
Learnables: {[1×4 dlarray]}
State: {}
To check your critic, use getValue to return the value of a given observation, using the current parameter vector.
v = getValue(critic,{5,[0.1 0.1 0.1]'})v = 60
Note that the critic does not enforce the set constraint for the discrete set element.
v = getValue(critic,{-3,[0.1 0.1 0.1]'})v = 12
Obtain values for a random batch of 5 observations.
getValue(critic,{ ...
rand([obsInfo(1).Dimension 5]), ...
rand([obsInfo(2).Dimension 5]) ...
})ans = 1×5
2.8718 0.6859 0.4322 1.5246 2.9352
You can now use the critic (along with an actor) to create an agent for the environment described by the given observation specification object. Examples of agents that can work with mixed observation spaces, and use a value function critic, are rlACAgent, rlPGAgent, rlPPOAgent. rlTRPOAgent does not support actors or critics that use custom basis functions.
For more information on creating approximator objects such as actors and critics, see Create Policies and Value Functions.
Version History
Introduced in R2022a
See Also
Functions
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)