Load Predefined Control System Environments
Reinforcement Learning Toolbox™ software provides several predefined environments representing dynamical systems that are often used as benchmark cases for control systems design.
You can use predefined control system environments to learn how to apply reinforcement learning to the control of physical systems, gain familiarity with Reinforcement Learning Toolbox software features, or test your own agents. You can also use the predefined control system environments as a starting point for developing your own control system environment.
To create your own custom environments instead, see Custom Environments.
In the predefined control system environments, the state and observation are predefined and belong to nonfinite numerical vector spaces, while the action, also predefined, can still belong to a finite set. The (deterministic) state transitions laws are derived by discretizing the dynamics of an underlying physical system.
Simulink® environments are environments that rely on an underlying model for the
calculation of the state transition, reward, and observation. These environments do not
support using reset and step functions. Some of the
predefined control system environments are Simulink environments.
By contrast, environments that instead rely on MATLAB® functions or objects for the calculation of the state transition, reward, and observation, are referred to as MATLAB environments.
Multiagent environments are environments in which you can train and simulate multiple agents together. Some of the predefined MATLAB and Simulink control system environments are multiagent environments. For more information on predefined multiagent environments, see Load Predefined Multiagent Environments.
To load the predefined MATLAB control system environments listed in this table, use the rlPredefinedEnv
function. Each predefined environment is available in two versions, one with a discrete action
space, and the other with a continuous action space.
| Environment | Agent Task |
|---|---|
| Double integrator | Control a second-order dynamic system using either a discrete or continuous action space. |
| Cart-pole | Balance a pole on a moving cart by applying forces to the cart using either a discrete or continuous action space. |
| Simple pendulum with image observation | Swing up and balance a simple pendulum using the pendulum image as an observation, with either a discrete or continuous action space. |
You can also load the following predefined Simulink environments using the rlPredefinedEnv
function. For these environments, rlPredefinedEnv creates a SimulinkEnvWithAgent
object. Each of these predefined environment is also available in two versions, one with a
discrete action space, and the other with a continuous action space.
| Environment | Agent Task |
|---|---|
| Simple pendulum Simulink model | Swing up and balance a simple pendulum by applying a torque to the pendulum, using either a discrete or continuous action space. |
| Cart-pole Simscape™ model | Balance a pole on a moving cart by applying forces to the cart using either a discrete or continuous action space. This environment relies on a Simulink model that uses Simscape blocks to model the system. |
You can also load predefined grid world environments. For more information, see Load Predefined Grid World Environments.
To learn how to create your own custom environment, see Create Custom Environment Using Step and Reset Functions, Create Custom Simulink Environments, and Create Custom Environment from Class Template.
MATLAB Double-Integrator Environment
The double-integrator environment is a predefined MATLAB environment in which the goal of the agent is to control the position (right-positive) of a mass in a frictionless mono-dimensional space by applying a force input. The system has a second-order dynamics that can be represented by a double integrator, that is, two integrators in series.
In this environment, a training or simulation episode ends when either of these events occurs:
The mass moves beyond a given threshold (by default, 5 meters) from the origin.
The norm of the state vector is less than a given threshold (by default, 0.01).
There are two double-integrator environment variants, which differ by the agent action space:
Discrete — The agent can apply a force of either Fmax, zero, or -Fmax to the cart, where Fmax is the
MaxForceproperty of the environment.Continuous — The agent can apply any force within the range [-Fmax,Fmax].
To create a double-integrator environment, use rlPredefinedEnv as
follows, depending on the action space:
Discrete action space:
env = rlPredefinedEnv("DoubleIntegrator-Discrete");env = DoubleIntegratorDiscreteAction with properties: Gain: 1 Ts: 0.1000 MaxDistance: 5 GoalThreshold: 0.0100 Q: [2×2 double] R: 0.0100 MaxForce: 2 State: [2×1 double]For an example showing how to train an agent to control a discrete double-integrator environment, see Train PG Agent with Custom Networks to Control Discrete Double Integrator. For an example comparing the most used discrete action space agents on this environment, see Compare Agents on the Discrete Double-Integrator Environment.
Continuous action space:
env = rlPredefinedEnv("DoubleIntegrator-Continuous")env = DoubleIntegratorContinuousAction with properties: Gain: 1 Ts: 0.1000 MaxDistance: 5 GoalThreshold: 0.0100 Q: [2×2 double] R: 0.0100 MaxForce: Inf State: [2×1 double]For an example showing how to train an agent to control a continuous double-integrator environment, see Compare DDPG Agent to LQR Controller. For an example comparing the most used continuous action space agents on this environment, see Compare Agents on the Continuous Double Integrator Environment.
Environment Visualization
You can visualize the double-integrator environment using the
plot function. The plot displays the mass as a red
rectangle.
plot(env)
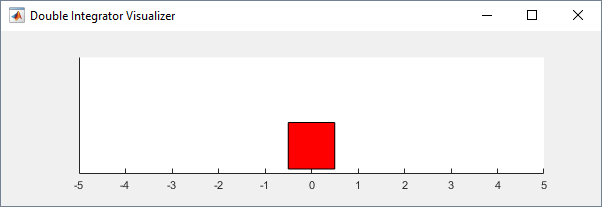
To visualize the environment during training, call plot before
training and keep the visualization figure open.
Note
While visualizing the environment during training might often be insightful, doing so tends to increase training time. For faster training, keep the environment plot closed during training.
Environment Properties
All the environment properties listed in this table are writable. You can change them to customize the double-integrator environment to your needs.
| Property | Description | Default |
|---|---|---|
Gain | Gain for the double integrator. This gain multiplies the force applied to the mass. | 1 |
Ts | Sample time in seconds. The software uses the sample time to discretize the dynamics of the underlying continuous-time system. The discrete-time dynamics is then used to calculate the next state as a function of the current state and of the applied action. | 0.1 |
MaxDistance | Distance magnitude threshold in meters. The episode terminates if the distance is greater than this threshold. | 5 |
GoalThreshold | State norm threshold. The episode terminates if the state is greater than this threshold. | 0.01 |
Q | Weight matrix for the observation component of the reward signal | [10 0; 0 1] |
R | Weight matrix for the action component of the reward signal | 0.01 |
MaxForce | Maximum input force in newtons. If the magnitude of the input force exceeds
this threshold, the magnitude of the force that is actually applied to the mass is
limited to MaxForce. | Discrete: Continuous:
|
State | Environment state, specified as a column vector with the following state variables:
| [0 0]' |
Dynamics
The continuous-time dynamics of this environment are described by this equation.
Here, p is the position of the mass, F is the
force applied by the agent, and k is the value of the
Gain property. The discrete-time dynamics is then obtained using
the zero-order hold approximation with sample time Ts. For more
information on the used discretization method, see lqrd (Control System Toolbox).
Actions
The agent interacts with the environment using an action channel carrying a single scalar, the force applied to the mass. The action space specification is as follows:
For the environment with discrete action space, the action channel specification is an
rlFiniteSetSpecobject.actInfo = getActionInfo(env)
actInfo = rlFiniteSetSpec with properties: Elements: [-2 0 2] Name: "force" Description: [0×0 string] Dimension: [1 1] DataType: "double"For the environment with a continuous action space, the action channel specification is an
rlNumericSpecobject.actInfo = getActionInfo(env)
actInfo = rlNumericSpec with properties: LowerLimit: -Inf UpperLimit: Inf Name: "force" Description: [0×0 string] Dimension: [1 1] DataType: "double"
For more information on obtaining action specifications from an environment, see
getActionInfo.
Observations
In the double-integrator system, the agent can observe both of the environment state
variables stored in env.State. The observation has a single channel,
specified by an rlNumericSpec
object, because both states are
continuous.
obsInfo = getObservationInfo(env)
obsInfo =
rlNumericSpec with properties:
LowerLimit: -Inf
UpperLimit: Inf
Name: "states"
Description: "x, dx"
Dimension: [2 1]
DataType: "double"
For more information on obtaining observation specifications from an environment, see
getObservationInfo.
Rewards
The reward signal , provided at every time step, is a discretization of :
where:
is the state vector of the system.
is the force applied to the mass.
is the weight matrix on the control performance, with default value .
is the weight matrix on the control effort, with default value .
In some control system applications, the reward signal is also referred to as the negative of the cost at stage k.
Note that is the instantaneous equivalent of this cumulative continuous-time reward, which is analogous to the cost function of an LQR controller:
For more information on the discretization of an LQR cost function, see lqrd (Control System Toolbox).
Reset Function
The reset function randomly sets the initial state of the environment so that the mass
is still and situated at 80% of MaxDistance in either the positive or
negative direction.
x0 = reset(env)
x0 =
4
0Unlike other environments, you cannot set your own reset function for a double-integrator environment.
Create a Default Agent for this Environment
The environment observation and action specifications allow you to create an agent that works with your environment. For example, for the discrete action space version of this environment, create a default PG agent.
pgAgent = rlPGAgent(obsInfo,actInfo)
pgAgent =
rlPGAgent with properties:
AgentOptions: [1×1 rl.option.rlPGAgentOptions]
UseExplorationPolicy: 1
ObservationInfo: [1×1 rl.util.rlNumericSpec]
ActionInfo: [1×1 rl.util.rlFiniteSetSpec]
SampleTime: 1
If needed, modify the agent options using dot notation.
pgAgent.AgentOptions.CriticOptimizerOptions.LearnRate = 1e-3; pgAgent.AgentOptions.ActorOptimizerOptions.LearnRate = 1e-3;
You can now use both the environment and the agent as arguments for the built-in
functions train and
sim, which train
or simulate the agent within the environment, respectively.
You can also create and train agents for this environment interactively using the Reinforcement Learning Designer app. For an example, see Design and Train Agent Using Reinforcement Learning Designer.
For more information on creating agents, see Reinforcement Learning Agents.
Step Function
You can also call the environment step function to return the next observation,
reward, and an is-done scalar indicating whether a final state has been
reached.
For example, call the step function with an input force of -10
N.
[xn,rn,id] = step(env,-10)
xn =
3.9500
-1.0000
rn =
-16.0005
id =
logical
0
The environment step and reset functions
allow you to create a custom training or simulation loop. For more information on custom
training loops, see Train Reinforcement Learning Policy Using Custom Training Loop.
Environment Code
To access the functions that returns the discrete action space version of this environment, at the MATLAB command line, type:
edit rl.env.DoubleIntegratorDiscreteActionTo access the function that returns the continuous action space version of this environment, at the MATLAB command line, type:
edit rl.env.DoubleIntegratorContinuousActionTo access the abstract class that contains the step function, at the MATLAB command line, type:
edit rl.env.DoubleIntegratorAbstractMATLAB Cart-Pole Environment
A MATLAB cart-pole environment is a predefined environment in which the goal of the agent is to balance a pole on a moving cart by applying a horizontal force to the cart. The pole is considered successfully balanced if both of these conditions are satisfied at the same time:
The pole angle (clockwise positive) remains within a given threshold of the vertical position, where the vertical position is zero radians.
The magnitude of the cart position (right positive) remains below a given threshold.
In this environment, a training or simulation episode ends when either of these events occurs:
The magnitude of the pole angle with respect to the vertical axis is more than a given threshold (by default, 12 degrees).
The cart moves more than a predefined threshold (by default, 2.4 meters) from the original position.
There are two cart-pole environment variants, which differ by the agent action space:
Discrete — The agent can apply a force of either Fmax or -Fmax to the cart, where Fmax is the
MaxForceproperty of the environment (by default, 10 newtons).Continuous — The agent can apply any force within the range [-Fmax,Fmax].
To create a cart-pole environment, use rlPredefinedEnv as
follows, depending on the desired action space:
Discrete action space:
env = rlPredefinedEnv("CartPole-Discrete")CartPoleDiscreteAction with properties: Gravity: 9.8000 MassCart: 1 MassPole: 0.1000 Length: 0.5000 MaxForce: 10 Ts: 0.0200 ThetaThresholdRadians: 0.2094 XThreshold: 2.4000 RewardForNotFalling: 1 PenaltyForFalling: -5 State: [4×1 double]For examples showing how to train an agent in this environments, see Train DQN Agent to Balance Discrete Cart-Pole System and Train PG Agent to Balance Discrete Cart-Pole System. For an example comparing the most used discrete action space agents on this environment, see Compare Agents on the Discrete Cart-Pole Environment.
Continuous action space:
env = rlPredefinedEnv("CartPole-Continuous")CartPoleContinuousAction with properties: Gravity: 9.8000 MassCart: 1 MassPole: 0.1000 Length: 0.5000 MaxForce: 10 Ts: 0.0200 ThetaThresholdRadians: 0.2094 XThreshold: 2.4000 RewardForNotFalling: 1 PenaltyForFalling: -50 State: [4×1 double]For an example showing how to train an agent in this environments, see Train MBPO Agent to Balance Continuous Cart-Pole System. For an example comparing the most used continuous action space agents on this environment, see Compare Agents on the Continuous Cart Pole.
Environment Properties
All the environment properties listed below are writable. You can change them to customize the cart-pole environment to your needs.
| Property | Description | Default |
|---|---|---|
Gravity | Acceleration due to gravity in meters per second squared | 9.8 |
MassCart | Mass of the cart in kilograms | 1 |
MassPole | Mass of the pole in kilograms | 0.1 |
Length | Distance from the pole hinge to the cart center of mass. If the pole density is uniform, this is half the length of the pole. | 0.5 |
MaxForce | Maximum horizontal force magnitude in newtons. If the magnitude of the input
force exceeds this threshold, the magnitude of the force that is actually applied
to the cart is limited to MaxForce. | 10 |
Ts | Sample time in seconds. The software uses the sample time to discretize the dynamics of the underlying continuous-time system. The discrete-time dynamics is then used to calculate the next state as a function of the current state and of the applied action. | 0.02 |
ThetaThresholdRadians | Pole angle threshold in radians. The episode terminates if the pole angle is greater than this threshold. | 0.2094 |
XThreshold | Cart position threshold in meters. The episode terminates if the cart position is greater than this threshold. | 2.4 |
RewardForNotFalling | Reward for each time step the pole is balanced | 1 |
PenaltyForFalling | Reward penalty for failing to balance the pole | Discrete — Continuous —
|
State | Environment state, specified as a column vector with these state variables:
| [0 0 0 0]' |
Visualization
You can visualize the cart-pole environment using the plot
function. The plot displays the cart as a blue square and the pole as a red
rectangle.
plot(env)
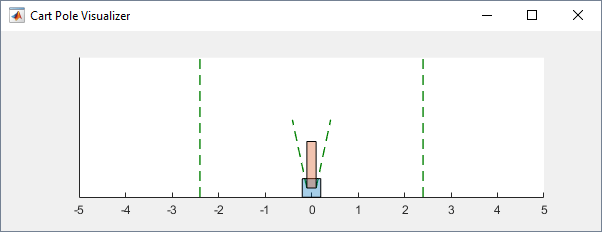
To visualize the environment during training, call plot before
training and keep the visualization figure open.
Note
While visualizing the environment during training might often be insightful, doing so tends to increase training time. For faster training, keep the environment plot closed during training.
Dynamics
The cart is subjected to an external input force and can move horizontally (the horizontal axis points right). Neither the cart nor the pole is subject to friction. The pole can rotate about the hinge on the upper surface of the cart (clockwise rotations are positive). Gravity acts vertically downwards. The center of gravity of the cart is at its geometrical center, and the center of gravity of the pole is at its half length. The continuous-time equations used to model this system are described in the Examples of Cart-Pole System in Reinforcement Learning Toolbox section of the example Derive Equations of Motion and Simulate Cart-Pole System (Symbolic Math Toolbox) and the reference [2] therein. The discrete-time dynamics of the environment are then obtained using the Euler integration method.
Actions
The agent interacts with the environment using an action channel carrying a single scalar, the horizontal force applied to the cart. The action space specification is as follows:
For an environment with a discrete action space, the action channel is specification is an
rlFiniteSetSpecobject.actInfo = getActionInfo(env)
rlFiniteSetSpec with properties: Elements: [-10 10] Name: "CartPole Action" Description: [0×0 string] Dimension: [1 1] DataType: "double"For an environment with a continuous action space, the action specification is an
rlNumericSpecobject.actInfo = getActionInfo(env)
rlNumericSpec with properties: LowerLimit: -10 UpperLimit: 10 Name: "CartPole Action" Description: [0×0 string] Dimension: [1 1] DataType: "double"
For more information on obtaining action specifications from an environment, see
getActionInfo.
Observations
In the cart-pole system, the agent can observe all the environment state variables
stored in env.State. The observation has a single channel specified
by an rlNumericSpec
object, because both signals are
continuous.
obsInfo = getObservationInfo(env)
obsInfo =
rlNumericSpec with properties:
LowerLimit: -Inf
UpperLimit: Inf
Name: "CartPole States"
Description: "x, dx, theta, dtheta"
Dimension: [4 1]
DataType: "double"For more information on obtaining observation specifications from an environment, see
getObservationInfo.
Reward
The reward signal for this environment is either:
A positive reward for each time step that the pole is balanced, that is, when the cart and pole both remain within their specified threshold ranges. This reward accumulates over the entire training episode. To control the size of this reward, use the
RewardForNotFallingproperty of the environment.A one-time negative penalty if either the pole or cart move outside of their threshold range. At this point, the training episode stops. To control the size of this penalty, use the
PenaltyForFallingproperty of the environment.
Reset Function
The reset function sets the initial state of the environment so that the cart position and velocity is zero, the pole angle is a random number between –0.05 and 0.05 radians, and the pole angular velocity is zero.
x0 = reset(env)
x0 =
0
0
0.0315
0Unlike other environments, you cannot set your own reset function for a cart-pole environment.
Create a Default Agent for this Environment
The environment observation and action specifications allow you to create an agent that works with your environment. For example, for the continuous action space version of this environment, create a default AC agent.
acAgent = rlACAgent(obsInfo,actInfo)
acAgent =
rlACAgent with properties:
AgentOptions: [1×1 rl.option.rlACAgentOptions]
UseExplorationPolicy: 1
ObservationInfo: [1×1 rl.util.rlNumericSpec]
ActionInfo: [1×1 rl.util.rlNumericSpec]
SampleTime: 1
If needed, modify the agent options using dot notation.
acAgent.AgentOptions.CriticOptimizerOptions.LearnRate = 1e-3; acAgent.AgentOptions.ActorOptimizerOptions.LearnRate = 1e-3;
You can now use both the environment and the agent as arguments for the built-in
functions train and
sim, which train
or simulate the agent within the environment, respectively.
You can also create and train agents for this environment interactively using the Reinforcement Learning Designer app. For an example, see Design and Train Agent Using Reinforcement Learning Designer.
For more information on creating agents, see Reinforcement Learning Agents.
Step Function
You can also call the environment step function to return the next observation,
reward, and an is-done scalar indicating whether a final state has been
reached.
For example, call the step function with an input force of 10
newtons.
[xn,rn,id] = step(env,10)
xn =
0
0.1947
0.0315
-0.2826
rn =
1
id =
logical
0The environment step and reset functions
allow you to create a custom training or simulation loop. For more information on custom
training loops, see Train Reinforcement Learning Policy Using Custom Training Loop.
Environment Code
To access the functions that returns the discrete action space version of this environment, at the MATLAB command line, type:
edit rl.env.CartPoleDiscreteActionTo access the function that returns the continuous action space version of this environment, at the MATLAB command line, type:
edit rl.env.CartPoleContinuousActionTo access the abstract class that contains the step function, at the MATLAB command line, type:
edit rl.env.CartPoleAbstractMATLAB Simple Pendulum Swing-Up with Image Observation Environment
A simple pendulum swing-up with image observation environment is a predefined MATLAB environment featuring a simple pendulum that initially hangs still in a downward position, that is, the initial angle of the pendulum is π and its initial angular speed is zero. The goal of the agent is to swing up the pendulum by applying an input torque and then keep the pendulum upright, using minimal control effort.
In this environment, the full state of the system (the angular position and the velocity of the pendulum) is not entirely available to the agent as an observation. Specifically, while the angular velocity is available in the second observation channel, the first observation channel carries a 50-by-50 pixel image representing the position of the pendulum center of mass. So, the agent also has to learn to estimate the pendulum angle from the image, as well as learning the right torque to apply to swing up the pendulum and keep it upright. As a consequence, agents built for this task normally feature one or more convolution networks, and training an agent in this environment is typically more computationally demanding than training an agent in simpler predefined environments.
There are two simple pendulum with image environment variants, which differ by the agent action space:
Discrete — The agent can apply a torque of
-2,-1,0,1, or2to the pendulum.Continuous — The agent can apply any torque within the range [
-2,2].
To create a simple pendulum environment, use rlPredefinedEnv as
follows, depending on the desired action space:
Discrete action space:
env = rlPredefinedEnv("SimplePendulumWithImage-Discrete")env = SimplePendlumWithImageDiscreteAction with properties: Mass: 1 RodLength: 1 RodInertia: 0 Gravity: 9.8100 DampingRatio: 0 MaximumTorque: 2 Ts: 0.0500 State: [2×1 double] Q: [2×2 double] R: 1.0000e-03For an example showing how to train an agent in this environments, see Create DQN Agent Using Deep Network Designer and Train Using Image Observations.
Continuous action space:
env = rlPredefinedEnv("SimplePendulumWithImage-Continuous")env = SimplePendlumWithImageContinuousAction with properties: Mass: 1 RodLength: 1 RodInertia: 0 Gravity: 9.8100 DampingRatio: 0 MaximumTorque: 2 Ts: 0.0500 State: [2×1 double] Q: [2×2 double] R: 1.0000e-03For an example showing how to train an agent in this environments, see Train DDPG Agent to Swing Up and Balance Pendulum with Image Observation.
Environment Visualization
You can visualize the simple pendulum with image environment using the
plot function. The main figure on the left side of the plot
displays the rod as a green line, and a black circle surrounding a blue dot indicates the
position of the rod center of mass. The plot also contains a smaller figure on the right
visualizing the content of the first observation channel, which is a 50-by-50 pixel image
with a black square representing the position of the pendulum center of mass.
plot(env)
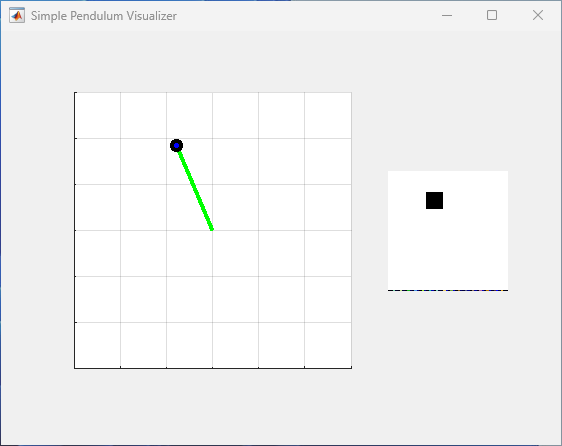
To visualize the environment during training, call plot before
training and keep the visualization figure open.
Note
While visualizing the environment during training might often be insightful, doing so tends to increase training time. For faster training, keep the environment plot closed during training.
Environment Properties
All the environment properties listed in this table are writable. You can change them to customize the simple pendulum with image environment to your needs.
| Property | Description | Default |
|---|---|---|
Mass | Pendulum mass in kilograms | 1 |
RodLength | Distance from the hinge to the pendulum center of mass in meters. For uniform rods, this distance is the half-length. | 1 |
RodInertia | Inertia moment of the rod (pendulum) about its center of mass in kilograms per meter squared | 0 |
Gravity | Acceleration due to gravity in meters per second squared | 9.81 |
DampingRatio | Damping on pendulum motion (viscous friction) in newtons per meter per second. | 0 |
MaximumTorque | Maximum input torque in newtons per meter. If the magnitude of the input
torque exceeds this threshold, the magnitude of the torque that is actually
applied to the pendulum is limited to MaximumTorque | 2 |
Ts | Sample time in seconds. The software uses the sample time to discretize the dynamics of the underlying continuous-time system. The discrete-time dynamics is then used to calculate the next state as a function of the current state and of the applied action. | 0.05 |
State | Environment state, specified as a column vector with these state variables:
| [0 0 ]' |
Q | Weight matrix for the observation component of reward signal | [1 0;0 0.1] |
R | Weight matrix for the action component of reward signal | 1e-3 |
Dynamics
The pendulum is a rigid rod subjected to an input torque (counterclockwise positive) and might be subjected to a viscous friction that counteracts the torque. The angle of rotation is counterclockwise positive and gravity acts vertically downwards. The center of gravity of the pendulum is at its half-length. The continuous-time equations used to model this system are described in the Simple Pendulum Equation section of the example Derive Equations of Motion and Simulate Cart-Pole System (Symbolic Math Toolbox). The discrete-time dynamics of the environment are then obtained using a trapezoidal integration method.
Actions
The agent interacts with the environment using an action channel carrying a single scalar, the torque applied at the base of the pendulum. The action space specification is as follows:
For environments with a discrete action space, the specification is an
rlFiniteSetSpecobject.actInfo = getActionInfo(env)
actInfo = rlFiniteSetSpec with properties: Elements: [-2 -1 0 1 2] Name: "torque" Description: [0×0 string] Dimension: [1 1] DataType: "double"For environments with a continuous action space, the specification is an
rlNumericSpecobject.actInfo = getActionInfo(env)
actInfo = rlNumericSpec with properties: LowerLimit: -2 UpperLimit: 2 Name: "torque" Description: [0×0 string] Dimension: [1 1] DataType: "double"
For more information on obtaining action specifications from an environment, see
getActionInfo.
Observations
In a simple pendulum environment with image environment, the agent receives the following observation signals:
50-by-50 grayscale image of the pendulum position
Derivative of the pendulum angle
The observation has two channels, each specified by an rlNumericSpec
object, because both signals are continuous.
obsInfo = getObservationInfo(env)
1×2 rlNumericSpec array with properties:
LowerLimit
UpperLimit
Name
Description
Dimension
DataType
obsInfo(1)
rlNumericSpec with properties:
LowerLimit: 0
UpperLimit: 1
Name: "pendImage"
Description: [0×0 string]
Dimension: [50 50]
DataType: "double"obsInfo(2)
rlNumericSpec with properties:
LowerLimit: -Inf
UpperLimit: Inf
Name: "angularRate"
Description: [0×0 string]
Dimension: [1 1]
DataType: "double"For more information on obtaining observation specifications from an environment, see
getObservationInfo.
Reward
The reward signal for this environment, at time t, is:
Here:
θt is the pendulum angle of displacement from the upright position (counterclockwise-positive, radians).
is the derivative of the pendulum angle with respect to time.
ut–1 is the control effort from the previous time step.
Reset Function
The reset function sets the initial state of the environment so that the pendulum is hanging downward and still.
reset(env); env.State
ans =
3.1416
0
Unlike other environments, you cannot set your own reset function for a simple pendulum with image environment.
Create a Default Agent for this Environment
The environment observation and action specifications allow you to create an agent that works with your environment. For example, for the discrete action space version of this environment, create a default DQN agent.
dqnAgent = rlDQNAgent(obsInfo,actInfo)
dqnAgent =
rlDQNAgent with properties:
ExperienceBuffer: [1×1 rl.replay.rlReplayMemory]
AgentOptions: [1×1 rl.option.rlDQNAgentOptions]
UseExplorationPolicy: 0
ObservationInfo: [1×2 rl.util.rlNumericSpec]
ActionInfo: [1×1 rl.util.rlFiniteSetSpec]
SampleTime: 1
If needed, modify the agent options using dot notation.
dqnAgent.AgentOptions.CriticOptimizerOptions.LearnRate = 1e-3;
You can now use both the environment and the agent as arguments for the built-in
functions train and
sim, which train
or simulate the agent within the environment, respectively.
You can also create and train agents for this environment interactively using the Reinforcement Learning Designer app. For an example, see Design and Train Agent Using Reinforcement Learning Designer.
For more information on creating agents, see Reinforcement Learning Agents.
Step Function
You can also call the environment step function to return the next observation,
reward, and an is-done scalar indicating whether a final state has been
reached.
For example, call the step function with an input torque of 1
newton per meter.
[xn,rn,id]=step(env,1)
xn =
1×2 cell array
{50×50 double} {[0.0500]}
rn =
-9.8630
id =
logical
0The environment step and reset functions
allow you to create a custom training or simulation loop. For more information on custom
training loops, see Train Reinforcement Learning Policy Using Custom Training Loop.
Environment Code
To access the functions that returns the discrete action space version of this environment, at the MATLAB command line, type:
edit rl.env.SimplePendlumWithImageDiscreteActionTo access the function that returns the continuous action space version of this environment, at the MATLAB command line, type:
edit rl.env.SimplePendlumWithImageContinuousActionTo access the abstract class that contains the step function, at the MATLAB command line, type:
edit rl.env.AbstractSimplePendlumWithImageSimulink Simple Pendulum Swing-up Environment
A simple pendulum swing-up environment is a predefined Simulink environment featuring a simple pendulum that initially hangs still in a downward position (that is, the initial angle of the pendulum is π and its initial angular speed is zero). The goal of the agent is to swing up the pendulum by applying an input torque and then keep the pendulum upright using minimal control effort.
The model for this environment is defined in the
rlSimplePendulumModel
Simulink model.
open_system("rlSimplePendulumModel")
There are two simple pendulum environment variants, which differ by the agent action space.
Discrete — The agent can apply a torque of either Tmax,
0, or -Tmax to the pendulum.Continuous — The agent can apply any torque within the range [-Tmax,Tmax].
Here, Tmax is the variable
max_tau, which you can change by accessing the workspace of the
rlSimplePendulumModel model. For more information on other variables
that you can change, see Dynamics. For more information on
Simulink model workspaces, see Model Workspaces (Simulink) and Change Model Workspace Data (Simulink).
To create a simple pendulum environment, use the rlPredefinedEnv as
follows, depending on the desired action space:
Discrete action space:
env = rlPredefinedEnv("SimplePendulumModel-Discrete")env = SimulinkEnvWithAgent with properties: Model : rlSimplePendulumModel AgentBlock : rlSimplePendulumModel/RL Agent ResetFcn : [] UseFastRestart : onFor an example of how to that train an agent in this environment, see Train DQN Agent to Swing Up and Balance Pendulum. For an example comparing the most used discrete action space agents on this environment, see Compare Agents on the Discrete Pendulum Swing-Up Environment.
Continuous action space:
env = rlPredefinedEnv("SimplePendulumModel-Continuous")env = SimulinkEnvWithAgent with properties: Model : rlSimplePendulumModel AgentBlock : rlSimplePendulumModel/RL Agent ResetFcn : [] UseFastRestart : onFor an example of how to that train an agent in this environment, see Train DDPG Agent to Swing Up and Balance Pendulum. For an example comparing the most used continuous action space agents on this environment, see Comparison of Agents on the Continuous Pendulum Swing-Up Environment.
Note
When training or simulating an agent within a Simulink environment, to ensure that the RL Agent block
executes at the desired sample time, set the SampleTime property of
the agent object appropriately.
For more information on Simulink environments, see SimulinkEnvWithAgent
and Create Custom Simulink Environments.
Environment Visualization
The environment is visualized with a plot that displays the pendulum as a green line and a black circle surrounding a blue dot indicating the position of the rod center of mass. The plot is displayed automatically by the Simulink model when it is executed by the simulation or training function.

Environment Properties
The environment properties that you can access using dot notation are described in
SimulinkEnvWithAgent.
Dynamics
The pendulum is a rigid rod subjected to an input counterclockwise-positive torque.
The pendulum might be subjected to a viscous friction that counteracts the torque. The
angle of rotation is counterclockwise positive and gravity acts vertically downward. The
center of gravity of the pendulum is at its half-length. For the exact continuous-time
equations used to model this system, see the Simple Pendulum
Equation section in the example Derive Equations of Motion and Simulate Cart-Pole System (Symbolic Math Toolbox). During simulation,
the Simulink solver then integrates the dynamics according to the selected solver, while
the RL Agent block
executes at discrete intervals according to the sample time specified in the
SampleTime property of the agent.
The pendulum dynamics are represented in the pendulum subsystem of the
rlSimplePendulumModel model, which calculates the pendulum angular
position and velocity as a function of the input force and of the previous state:

The parameters that define the pendulum dynamics are stored in the workspace of the
rlSimplePendulumModel model.
| Variable | Description | Default |
|---|---|---|
I | Inertia moment of the rod (pendulum) about its center of mass in kilograms per meter squared | 0 |
c | Torque damping on pendulum motion (viscous friction) in newtons per meter per second. | 0 |
g | Acceleration due to gravity in meters per second squared | 9.81 |
l | Distance from the hinge to the pendulum center of mass in meters. For uniform rods, this distance is the half-length. | 1 |
m | Pendulum mass in kilograms | 1 |
max_tau | Maximum input torque in newtons per meter. If the magnitude of the input
torque exceeds this threshold, the magnitude of the torque that is actually
applied to the pendulum is limited to MaximumTorque. | 2 |
theta0 | Initial value of the pendulum angle (counterclockwise-positive). The reset
function normally sets this value topi. | 0 |
theta_dot0 | Initial value of the pendulum angular speed. The reset function normally sets
this value to 0. | 0 |
For more information on Simulink model workspaces, see Model Workspaces (Simulink) and Change Model Workspace Data (Simulink).
Actions
The agent interacts with the environment using an action channel carrying a single scalar, the torque applied at the base of the pendulum. The action space specification is as follows:
For an environment with a discrete action space, the specification is an
rlFiniteSetSpecobject.actInfo = getActionInfo(env)
actInfo = rlFiniteSetSpec with properties: Elements: [3×1 double] Name: "torque" Description: [0×0 string] Dimension: [1 1] DataType: "double"actInfo.Elements'
ans = -2 0 2For an environment with a continuous action space, the specification is an
rlNumericSpecobject.actInfo = getActionInfo(env)
actInfo = rlNumericSpec with properties: LowerLimit: -2 UpperLimit: 2 Name: "torque" Description: [0×0 string] Dimension: [1 1] DataType: "double"
For more information on obtaining action specifications from an environment, see
getActionInfo.
Observations
In a simple pendulum swing-up with Simulink environment, the observation is calculated within the create
observations subsystem of the rlSimplePendulumModel
model.
The agent receives these observation signals:
Sine of the pendulum angle
Cosine of the pendulum angle
Derivative of the pendulum angle with respect to time
The observation has a single channel specified by an rlNumericSpec
object, because the three observation signals are
continuous.
obsInfo = getObservationInfo(env)
obsInfo =
rlNumericSpec with properties:
LowerLimit: -Inf
UpperLimit: Inf
Name: "observations"
Description: [0×0 string]
Dimension: [3 1]
DataType: "double"For more information on obtaining observation specifications from an environment, see
getObservationInfo.
Reward
In this environment, the reward is calculated within the calculate
reward subsystem of the rlSimplePendulumModel model.

The reward is
Here:
θt is the pendulum angle of displacement (counterclockwise-positive) from the upright position.
is the derivative of the pendulum angle with respect to time.
ut–1 is the control effort from the previous time step.
Reset Function
The environment has no default reset function. However, you can
set your own reset function to set the initial state of the pendulum
every time a simulation starts to train or simulate the environment.
For example, to set the initial condition of the pendulum as still and hanging
downward, specify the handle of an anonymous reset function that sets the model workspace
variable theta0 to pi.
env.ResetFcn = @(in)setVariable(in,
"theta0",pi, ...
"Workspace","rlSimplePendulumModel");Here, you use setVariable (Simulink)
to set the variable theta0 to a random value in the Simulink.SimulationInput (Simulink) object in. The value of
theta0 that you specify overrides the existing
theta0 value in the model workspace for the duration of the
simulation or training. The value of theta0 then reverts to its
original value when the simulation or training completes.
Create a Default Agent for this Environment
The environment observation and action specifications allow you to create an agent that works with your environment. For example, for the continuous action space version of this environment, create a default PPO agent.
agent = rlPPOAgent(obsInfo,actInfo)
agent =
rlPPOAgent with properties:
AgentOptions: [1×1 rl.option.rlPPOAgentOptions]
UseExplorationPolicy: 1
ObservationInfo: [1×1 rl.util.rlNumericSpec]
ActionInfo: [1×1 rl.util.rlNumericSpec]
SampleTime: 1
Set the agent sample time so that the RL Agent block executes at the desired rate.
agent.SampleTime = 0.05;
If needed, modify the agent options using dot notation.
agent.AgentOptions.CriticOptimizerOptions.LearnRate = 1e-3; agent.AgentOptions.ActorOptimizerOptions.LearnRate = 1e-3;
You can now use both the environment and the agent as arguments for the built-in
functions train and
sim, which train
or simulate the agent within the environment, respectively.
You can also create and train agents for this environment interactively using the Reinforcement Learning Designer app. For an example, see Design and Train Agent Using Reinforcement Learning Designer.
For more information on creating agents, see Reinforcement Learning Agents.
Step Function
Because this is a Simulink environment, calling the step function is not
supported. For an example on how to build a custom training loop using a Simulink environment, see Custom Training Loop with Simulink Action Noise.
Simscape Cart-Pole Swing-up Environment
A Simscape cart-pole swing-up environment is a predefined Simulink environment featuring a cart-pole system modeled using Simscape Multibody™. The pole initially hangs still in a downward position (that is, the initial angle is π radians and the initial angular speed is zero). The goal of the agent is to swing up the pole by applying an input force on the cart and then maintain the pole upright using minimal control effort. The episode terminates if the cart moves more than 3.5 meters from the original position.
The model for this environment is defined in the
rlCartPoleSimscapeModel
Simulink model.
open_system("rlCartPoleSimscapeModel")
In the Environment subsystem, the model dynamics are defined within the Plant subsystem, using Simscape components. The reward and is-done signals are defined in the qr reward and x limit penalty subsystems, respectively, using Simulink blocks. The black multiplexer block aggregates the observations into a single observation signal.
open_system("rlCartPoleSimscapeModel/Environment")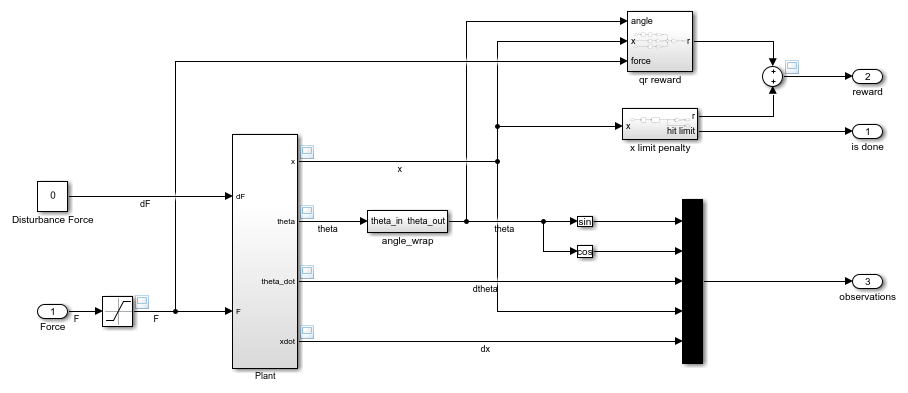
There are two variants of this environment, which differ by the agent action space:
Discrete — The agent can apply a force of
15,0, or-15newtons to the cart.Continuous — The agent can apply any force within the range [
-15,15] newtons.
To create a cart-pole environment, use rlPredefinedEnv as
follows, depending on the desired action space:
Discrete action space:
env = rlPredefinedEnv("CartPoleSimscapeModel-Discrete")env = SimulinkEnvWithAgent with properties: Model : rlCartPoleSimscapeModel AgentBlock : rlCartPoleSimscapeModel/RL Agent ResetFcn : [] UseFastRestart : onFor an example comparing the most used discrete action space agents on this environment, see Compare Agents on the Discrete Simscape Cart-Pole Swing-Up Environment.
Continuous action space:
env = rlPredefinedEnv("CartPoleSimscapeModel-Continuous")env = SimulinkEnvWithAgent with properties: Model : rlCartPoleSimscapeModel AgentBlock : rlCartPoleSimscapeModel/RL Agent ResetFcn : [] UseFastRestart : onFor an example that trains an agent in this cart-pole environment, see Train DDPG Agent to Swing Up and Balance Cart-Pole System. For an example comparing the most used discrete action space agents on this environment, see Compare Agents on the Continuous Cart Pole Swing-Up Environment.
Note
When training or simulating an agent within a Simulink environment, to ensure that the RL Agent block
executes at the desired sample time, set the SampleTime property of
the agent object appropriately.
For more information on Simulink environments, see SimulinkEnvWithAgent
and Create Custom Simulink Environments.
Environment Visualization
The environment visualization shows the cart and the pole as gray and red rectangles, respectively, and it is displayed automatically in the Mechanics Explorer by the Simulink model when it is executed by the simulation or training function.

Environment Properties
The environment properties that you can access using dot notation are described in
SimulinkEnvWithAgent.
Dynamics
The cart is subjected to an external input force as well as viscous friction and can
move horizontally (the horizontal axis points right). The pole is not subject to friction
and can rotate about the hinge on the cart (counterclockwise rotations are positive).
Gravity acts vertically downwards. For the exact continuous-time equations used to model
this system, see the Examples of Cart-Pole System in Simscape
Multibody section in the example Derive Equations of Motion and Simulate Cart-Pole System (Symbolic Math Toolbox). During simulation,
the Simulink solver integrates the dynamics according to the selected solver, while the
RL Agent block
executes at discrete intervals according to the sample time specified in the
SampleTime property of the agent.
The continuous-time system dynamics are represented using Simscape
Multibody in the Plant subsystem of the
rlCartPoleSimscapeModel model. This subsystem calculates the linear
and angular positions and velocities of the cart and pole, respectively, as a function of
the input force on the cart and of the previous state:

The parameters that define the system dynamics are stored in the workspace of the
rlCartPoleSimscapeModel model.
| Variable | Description | Default |
|---|---|---|
mCart | Mass of the cart in kilograms | 1 |
mPend | Mass of the pole in kilograms | 1 |
Gravity | Acceleration due to gravity in meters per second squared | 9.8 |
Length | Distance from the pole hinge to the cart center of mass. If the pole density is uniform, this distance is half the length of the pole. | 0.5 |
theta0 | Initial value of the pendulum angle (counterclockwise-positive) in degrees. | 180 |
Kd | Force damping on cart motion (viscous friction) in newtons per second over meter. | 10 |
For more information on Simulink model workspaces, see Model Workspaces (Simulink) and Change Model Workspace Data (Simulink).
Actions
The agent interacts with the environment using an action channel carrying a single scalar, the horizontal force applied to the cart. The action space specification is as follows:
Discrete action space, the channel is specified by an
rlFiniteSetSpecobject.actInfo = getActionInfo(env)
actInfo = rlFiniteSetSpec with properties: Elements: [3×1 double] Name: "force" Description: [0×0 string] Dimension: [1 1] DataType: "double"actInfo.Elements'
ans = -15 0 15
Continuous action space, the channel is specified by an
rlNumericSpecobject.actInfo = getActionInfo(env)
actInfo = rlNumericSpec with properties: LowerLimit: -15 UpperLimit: 15 Name: "force" Description: [0×0 string] Dimension: [1 1] DataType: "double"
For more information on obtaining action specifications from an environment, see
getActionInfo.
Observations
In this environment, the observations are aggregated using a multiplexer block within
the Environment subsystem of the rlCartPoleSimscapeModel
model. The agent receives the following five observation signals.
Sine of the pole angle
Cosine of the pole angle
Derivative of the pendulum angle
Cart position
Derivative the of cart position
The observation has a single channel, specified by an rlNumericSpec
object, because the five observation signals are
continuous,
obsInfo = getObservationInfo(env)
obsInfo =
rlNumericSpec with properties:
LowerLimit: -Inf
UpperLimit: Inf
Name: "observations"
Description: [0×0 string]
Dimension: [5 1]
DataType: "double"For more information on obtaining observation specifications from an environment, see
getObservationInfo.
Reward
In this environment, the reward is calculated within the qr reward subsystem.
The reward signal for this environment is the sum of two components (r = rqr + rn + rp):
A quadratic regulator control reward, constructed in the
Environment/qr rewardsubsystem:A cart limit penalty, constructed in the
Environment/x limit penaltysubsystem. This subsystem generates a negative reward when the magnitude of the cart position exceeds a given threshold:
Here:
x is the cart position.
θ is the pole angle of displacement from the upright position.
ut–1 is the control effort from the previous time step.
Reset Function
The environment has no default reset function. However, you can
set your own reset function to set the initial state of the system
every time a simulation starts to train or simulate the environment.
For example, to set the initial pole to a random angle between 180 and –180 degrees,
instead of the default value of 180 degrees, specify the handle of an anonymous reset
function that sets the model workspace variable theta0 to
360*rand-180.
env.ResetFcn = @(in)setVariable(in, ... "theta0",360*rand-180, ... "Workspace","rlCartPoleSimscapeModel");
Here, you use setVariable (Simulink)
to set the variable theta0 to a random value in the Simulink.SimulationInput (Simulink) object in. The value of
theta0 that you specify overrides the existing
theta0 value in the model workspace for the duration of the
simulation or training. The value of theta0 then reverts to its
original value when the simulation or training completes.
Create a Default Agent for this Environment
The environment observation and action specifications allow you to create an agent that works with your environment. For example, for the discrete action space version of this environment, create a default SAC agent.
agent = rlSACAgent(obsInfo,actInfo)
agent =
rlSACAgent with properties:
ExperienceBuffer: [1×1 rl.replay.rlReplayMemory]
AgentOptions: [1×1 rl.option.rlSACAgentOptions]
UseExplorationPolicy: 1
ObservationInfo: [1×1 rl.util.rlNumericSpec]
ActionInfo: [1×1 rl.util.rlFiniteSetSpec]
SampleTime: 1Set the agent sample time so that the RL Agent block executes at the desired rate.
agent.SampleTime = 0.02;
If needed, modify the agent options using dot notation.
agent.AgentOptions.CriticOptimizerOptions(1).LearnRate = 1e-3; agent.AgentOptions.CriticOptimizerOptions(2).LearnRate = 1e-3; agent.AgentOptions.ActorOptimizerOptions.LearnRate = 1e-3;
You can now use both the environment and the agent as arguments for the built-in
functions train and
sim, which train
or simulate the agent within the environment, respectively.
You can also create and train agents for this environment interactively using the Reinforcement Learning Designer app. For an example, see Design and Train Agent Using Reinforcement Learning Designer.
For more information on creating agents, see Reinforcement Learning Agents.
Step Function
Because this is a Simulink environment, calling the step function is not
supported. For an example on how to build a custom training loop using a Simulink environment, see Custom Training Loop with Simulink Action Noise.
See Also
Functions
rlPredefinedEnv|getObservationInfo|getActionInfo|train|sim|reset