Train Reinforcement Learning Agent for Simple Contextual Bandit Problem

Fix Random Seed Generator to Improve Reproducibility

The example code may involve computation of random numbers at various stages such as initialization of the agent, creation of the actor and critic, resetting the environment during simulations, initializing the environment state, generating observations (for stochastic environments), generating exploration actions, and sampling minibatches of experiences for learning. Fixing the random number stream preserves the sequence of the random numbers every time you run the code and improves reproducibility of results. You will fix the random number stream at various locations in the example.

Fix the random number stream with the seed 0 and random number algorithm Mersenne Twister. For more information on random number generation see rng.

previousRngState = rng(0,"twister");

The output previousRngState is a structure that contains information about the previous state of the stream. You will restore the state at the end of the example.

Environment

The contextual bandit environment in this example is defined as follows:

The context (initial observation) is sampled randomly.

Rewards in this environment are stochastic. The probability of each observation and action pair is defined as follows.

Note that the agent does not know these distributions.

Create Environment Object

The contextual bandit environment is implemented in the file ToyContextualBanditEnvironment, located in this example folder. For more information on how to implement a custom environment using the class template, see Create Custom Environment from Class Template.

Display the environment class. Note how the rewards are calculated in the environment step function, and how the observation (context) remains constant at its initial value.

type("ToyContextualBanditEnvironment.m")

classdef ToyContextualBanditEnvironment < rl.env.MATLABEnvironment
    
    %% Properties (set properties' attributes accordingly)    
    properties
        % Initialize state
        State = zeros(1,1)
    end
    
    properties(Access = protected)
        % Initialize internal flag to indicate episode termination.
        IsDone = false        
    end

    %% Necessary Methods
    methods              
        % Constructor method creates an instance of the environment.
        % Change class name and constructor name accordingly.
        function this = ToyContextualBanditEnvironment()
            % Initialize Observation settings
            % Observation = {s1, s2}, discrete
            obsInfo = rlFiniteSetSpec([1 2]);
            
            % Initialize Action settings
            % Action = {a1, a2, a3}, discrete
            actInfo = rlFiniteSetSpec([1 2 3]);            
            
            % Implement built-in functions of RL env
            this = this@rl.env.MATLABEnvironment(obsInfo,actInfo);
        end
        
        % Apply system dynamics and simulate the environment
        % with the given action for one step.
        function [Observation,Reward,IsDone,aux] = step(this,Action)
            aux = [];

            % The action doesn't affect the next state
            % in a contextual bandit problem.
            Observation = this.State;
            
            % Get reward            
            if this.State == 1
                if Action == 1
                    % E(reward) = 2.9
                    if rand < 0.3
                        Reward = 5;
                    else
                        Reward = 2;
                    end
                elseif Action == 2
                    % E(reward) = 1.9
                    if rand < 0.1
                        Reward = 10;
                    else
                        Reward = 1;
                    end
                elseif Action == 3
                    % E(reward) = 3.5
                    Reward = 3.5;                    
                end
            elseif this.State == 2
               if Action == 1
                   % E(reward) = 3.6
                   if rand < 0.2
                       Reward = 10;
                   else
                       Reward = 2;
                   end
               elseif Action == 2
                   % E(reward) = 3.0
                   Reward = 3.0;               
               elseif Action == 3
                   % E(reward) = 3
                   if rand < 0.5
                        Reward =  5;
                   else
                        Reward = 0.5;
                   end
               end         
            end            
            
            % Get IsDone.
            IsDone = true;
            this.IsDone = IsDone;
            % (Optional) Use notifyEnvUpdated to signal 
            % that the environment has been updated 
            % (e.g. to update visualization).
            notifyEnvUpdated(this);
        end
        
        % Reset environment to initial state 
        % and output initial observation.
        function InitialObservation = reset(this)
            % Pr(s1) = 0.5, Pr(s2) = 0.5
            InitialObservation = randi(2);
            this.State = InitialObservation;

            % (Optional) Use notifyEnvUpdated to signal 
            % that the environment has been updated 
            % (e.g. to update visualization).
            notifyEnvUpdated(this);
        end
    end
    %% Optional Methods (set methods' attributes accordingly)
    methods               
        % (Optional) Visualization method
        function plot(this)            
            % Update the visualization
            envUpdatedCallback(this)
        end
        
        % (Optional) Properties validation through set methods
        function set.State(this,state)
            mustBeMember(state,[1,2])
            this.State = state;
            notifyEnvUpdated(this);
        end
    end    
end

Create the environment object.

env = ToyContextualBanditEnvironment;

Get observation and action specification objects.

obsInfo = getObservationInfo(env);
actInfo = getActionInfo(env);

Create a DQN Agent

Create a DQN agent option object. For more information, see rlDQNAgentOptions.

agentOpts = rlDQNAgentOptions(...
    UseDoubleDQN = false, ...    
    TargetSmoothFactor = 1, ...
    TargetUpdateFrequency = 4, ...     
    MiniBatchSize = 64,...
    MaxMiniBatchPerEpoch = 2);
agentOpts.EpsilonGreedyExploration.EpsilonDecay = 0.0005;

To create an agent with default network structure, in which each hidden layer has 16 neurons, use rlAgentInitializationOptions.

initOpts = rlAgentInitializationOptions(NumHiddenUnit = 16);

Create a DQN agent. For more information, see rlDQNAgent.

dqnAgent = rlDQNAgent(obsInfo, actInfo, initOpts, agentOpts);

Train the DQN Agent

To train the agent, first specify the training options. For this example, use the following options:

For more information, see rlTrainingOptions.

trainOpts = rlTrainingOptions(...
    MaxEpisodes=3000, ...
    MaxStepsPerEpisode=1, ...
    Verbose=false, ...
    Plots="training-progress",...
    StopTrainingCriteria="None",...
    StopTrainingValue="None"); 

Train the agent using the train function. Training is a computationally intensive process that takes several minutes to complete. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.

doTraining = false;
if doTraining
    % Train the agent
    trainingStats = train(dqnAgent,env,trainOpts);
else
    % Load the pretrained agent for the example
    load("ToyContextualBanditDQNAgent.mat","dqnAgent")
end

Validate the DQN Agent

For this example, you know the distribution of the rewards, and you can compute the optimal actions. Validate the agent's performance by comparing these optimal actions with the actions selected by the agent.

First, compute the true expected rewards using their true probability distribution.

1. The expected reward of each action at s=1 is as follows.

Hence, the optimal action is 3 when s=1.

2. The expected reward of each action at s=2 is as follows.

Hence, the optimal action is 1 when s=2.

With enough sampling, the Q-value estimates of the trained agent should be closer to the true expected reward.

Collect the true expected rewards in the ExpectedRewards variable.

ExpectedRewards = zeros(2,3);
ExpectedRewards(1,1) = 0.3*5 + 0.7*2;
ExpectedRewards(1,2) = 0.1*10 + 0.9*1;
ExpectedRewards(1,3) = 3.5;
ExpectedRewards(2,1) = 0.2*10 + 0.8*2;
ExpectedRewards(2,2) = 3.0;
ExpectedRewards(2,3) = 0.5*5 + 0.5*0.5;

Visualize the true expected rewards using the function localPlotQvalues defined at the end of the example.

localPlotQvalues(ExpectedRewards,"True Expected Rewards")

Now, validate whether the DQN agent learns the optimal behavior. Use getActionInfo to return the agent action given an input observation.

If the state is 1, the optimal action is 3.

observation = 1;
getAction(dqnAgent,observation)

ans = 1x1 cell array
    {[3]}

The agent selects the optimal action.

If the state is 2, the optimal action is 1.

observation = 2;
getAction(dqnAgent,observation)

ans = 1x1 cell array
    {[1]}

The agent selects the optimal action. Thus, the DQN agent has learned the optimal behavior.

Next, compare the Q-Value function to the true expected reward when selecting the optimal action.

Use getCritic to extract the critic from the trained agent, and getValue to return the value of an observation (using the learned value function).

dqnCritic = getCritic(dqnAgent);
qValues = zeros(2,3);
for s = 1:2
    qValues(s,:) = getValue(dqnCritic, {s});
end

Visualize the Q values for the DQN agent.

figure(1)
localPlotQvalues(qValues, "Q values of DQN agent")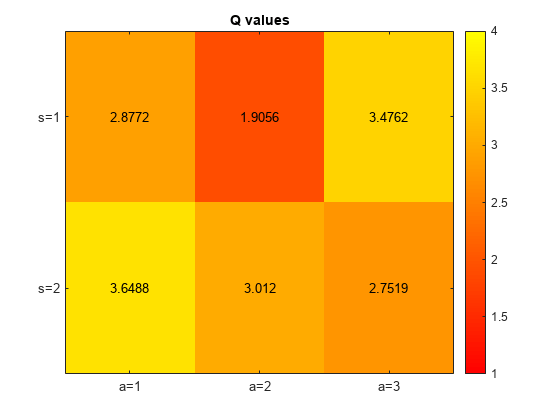

The learned Q-values are close to the true expected rewards computed above.

Create a Q-Learning Agent

Ensure reproducibility by fixing the random seed generation.

rng(0,"twister")

For this example, use a table as approximation model for the critic.

Create a table using the observation and action specifications from the environment.

qTable = rlTable(obsInfo, actInfo);

Create an rlQValueFunction critic.

critic = rlQValueFunction(qTable, obsInfo, actInfo);

To set the agent exploration options, create an rlQAgentOptions object

opt = rlQAgentOptions;
opt.EpsilonGreedyExploration.Epsilon = 1;
opt.EpsilonGreedyExploration.EpsilonDecay = 0.0005;

Create a Q agent. For more information, see rlQAgent.

qAgent = rlQAgent(critic,opt);

Train the Q-Learning Agent

To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.

doTraining = false;
if doTraining
    % Train the agent.
    trainingStats = train(qAgent,env,trainOpts);
else
    % Load the pretrained agent for the example.
    load("ToyContextualBanditQAgent.mat","qAgent")
end

Validate the Q-Learning Agent

When the state is 1, the optimal action is 3.

observation = 1;
getAction(qAgent,observation)

ans = 1x1 cell array
    {[3]}

The agent selects the optimal action.

When the state is 2, the optimal action is 1.

observation = 2;
getAction(qAgent,observation)

ans = 1x1 cell array
    {[1]}

The agent selects the optimal action.

Next, compare the Q-Value function to the true expected reward when selecting the optimal action.

Use getCritic to extract the critic from the trained agent, and getValue to return the value of an observation (using the learned value function).

figure(2)
qCritic = getCritic(qAgent);
qValues = zeros(2,3);
for s = 1:2
    for a = 1:3
        qValues(s,a) = getValue(qCritic, {s}, {a});
    end
end

Visualize the Q values for the DQN agent.

localPlotQvalues(qValues, "Q values of Q agent")

The learned Q-values are close to the true expected rewards. The Q-values for deterministic rewards, Q(s=1, a=3) and Q(s=2, a=2), are the same as the true expected rewards.

Note that the corresponding Q-values learned by the DQN network, while close, are not identical to the true values. This happens because the DQN uses a neural network instead of a table as function approximation model.

Restore the random number stream using the information stored in previousRngState.

rng(previousRngState);

Local Function

function localPlotQvalues(QValues, titleText)
    % Visualize Q values 
    figure;
    imagesc(QValues,[1,4])
    colormap("autumn")
    title(titleText)
    colorbar
    set(gca,"Xtick",1:3,"XTickLabel",{"a=1", "a=2", "a=3"})
    set(gca,"Ytick",1:2,"YTickLabel",{"s=1", "s=2"})

    % Plot values on the image
    x = repmat(1:size(QValues,2), size(QValues,1), 1);
    y = repmat(1:size(QValues,1), size(QValues,2), 1)';
    QValuesStr = num2cell(QValues);
    QValuesStr = cellfun(@num2str, QValuesStr, UniformOutput=false);
    text(x(:), y(:), QValuesStr, HorizontalAlignment = "Center")
end

Reference

[1] Sutton, Richard S., and Andrew G. Barto. Reinforcement Learning: An Introduction. Second edition. Adaptive Computation and Machine Learning Series. Cambridge, Massachusetts: The MIT Press, 2018.