Main Content

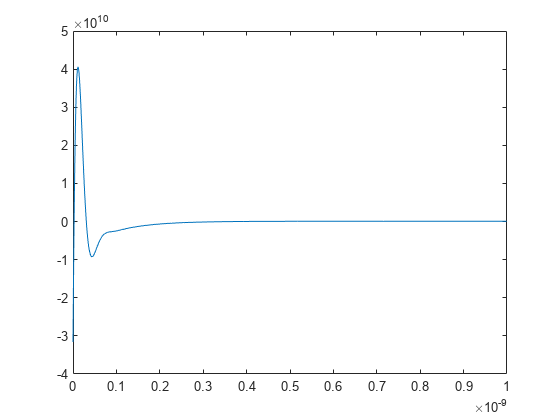
impulse

Impulse response for rational function object

collapse all in page

Syntax

[response,tout] = impulse(h,ts,n)

Description

[response,tout] = impulse(h,ts,n) computes the impulse response of a rational function object, h, over a time period specified by ts and the number of samples n.

Note

While you can compute the output response for a rational function object by computing the impulse response of the object and then convolving that response with the input signal, this approach is not recommended. Instead, you should use the timeresp method to perform this computation because it generally gives a more accurate output signal for a given input signal.

example

Examples

collapse all

Open Live Script

Create a sparameters object from a file and use rfparam to extract the S21parameters.

S = sparameters('passive.s2p');
S21 = rfparam(S,2,1);

Fit a rational function object to the S21 data by using rationalfit.

freq = S.Frequencies;
fit_data = rationalfit(freq,S21)
fit_data = 
   rfmodel.rational with properties:

        A: [6x1 double]
        C: [6x1 double]
        D: 0
    Delay: 0
     Name: 'Rational Function'

Calculate the impulse response using the impulse method and plot the results.

[resp,t] = impulse(fit_data,1e-12,1e3);
plot(t,resp);

Figure contains an axes object. The axes object contains an object of type line.

Open Live Script

Perform rational fitting on a S-parameters object to create a rational function.

S = sparameters('passive.s2p');
fit = rational(S);

Compute the impulse response using the impulse method.

[resp,t] = impulse(fit,1e-12,1e2)
resp=2×2 cell array
    {100x1 double}    {100x1 double}
    {100x1 double}    {100x1 double}


t=2×2 cell array
    {100x1 double}    {100x1 double}
    {100x1 double}    {100x1 double}

Plot the results of the S21 data.

plot(t{2,1},resp{2,1})
xlabel('Frequency (Hz)');
ylabel('Impulse Response of S21');

Figure contains an axes object. The axes object with xlabel Frequency (Hz), ylabel Impulse Response of S21 contains an object of type line.

Input Arguments

collapse all

Rational function object, specified as a rationalfit or a rational object.

Data Types: double
Complex Number Support: Yes

Sample time of the computed impulse response, specified as a positive scalar integer in seconds.

Data Types: double

Number of samples in the impulse response, specified as a positive scalar integer.

Data Types: double

Output Arguments

collapse all

Computed impulse response, returned as an n element real vector of impulse response values.

Sample time of the output signal, returned as a nonnegative vector of time values with discrete step size ts corresponding to the data in response in seconds.

Data Types: double

More About

collapse all

Impulse Response And Time Samples Equation

RF Toolbox™ uses the following equation to for the impulse response:

resp=∑k=1MCkeAk(t−Delay)u(t−Delay)+Dδ(t−Delay)

where

  • A, C, D, and Delay are properties of the rational function object, h.

  • M is the number of poles in the rational function object.

The vector of time samples of the impulse response, t, is computed from the inputs as t = [0,ts,2*ts,...,(n-1)*ts]

Version History

Introduced in R2006b

See Also

| | | | | |