rational

Perform rational fitting on complex frequency-dependent data

Since R2020a. Recommended over rationalfit.

Description

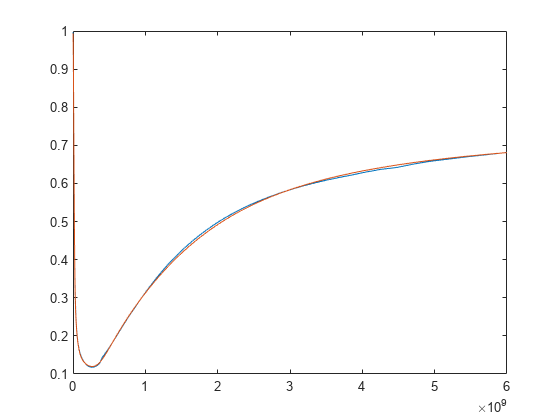
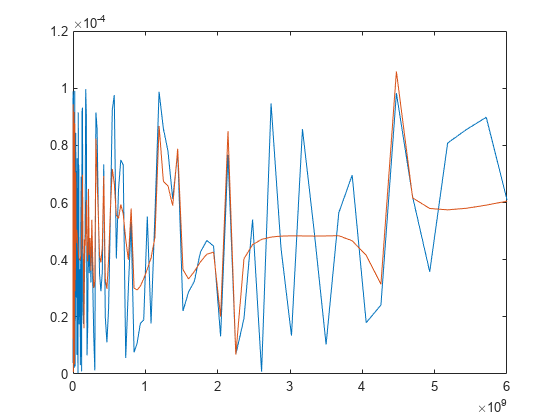
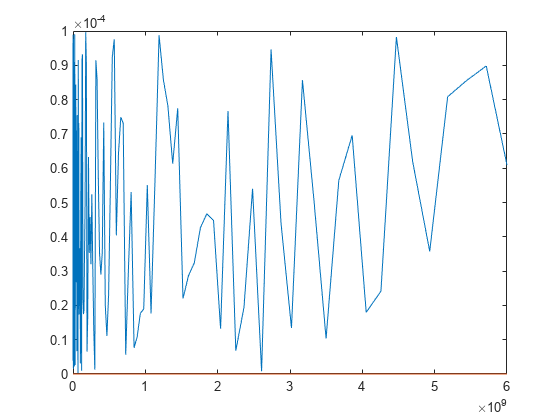
Use the rational object to perform rational fitting on complex frequency-dependent data. This object uses a non-iterative interpolatory algorithm to construct a fit with complex frequencies s. The fit of the each element of the rational object is given by this equation:

$\begin{array}{l} F (s) = \sum_{k = 1}^{n} \frac{C_{k}}{s - A_{k}} + D, \\ where: \\ s = j \times 2 π f \\ C - R esidues \\ A - P oles \\ D - D irect term \end{array}$

Creation

Syntax

fit = rational

fit = rational(freq,data)

fit = rational(s)

fit = rational(filename)

fit = rational(___,tol)

fit = rational(___,Name=Value)

[fit,errdb] = rational(___)

Description

fit = rational creates a non-reflective one-port rational object with default properties.

fit = rational(freq,data) performs rational fitting for the given frequency vector freq and network parameter data data.

fit = rational(s) performs rational fitting for the N-port S-parameters object s.

example

fit = rational(filename) performs rational fitting of network data in the file specified in filename.

fit = rational(___,tol) strives to satisfy the relative error tolerance tol when performing rational fit.

fit = rational(___,Name=Value) specifies options to control aspects of the fit or sets properties of the rational object. You can also set the NumPoles, Poles, Residues, and DirectTerm properties (since R2023a) using name-value arguments. For example, fit = rational(s,MaxPoles=1002) sets the maximum number of poles for the fit. Specify name-value arguments after any of the input arguments from the previous syntaxes.

example

[fit,errdb] = rational(___) also returns the error of the fit errdb.

Input Arguments

expand all

`freq` — Nonnegative frequencies
vector

Nonnegative frequencies, specified as a vector of nonnegative frequencies in Hz.

Data Types: double

`data` — Network parameter data
vector | 2-D array | 3-D array

Network parameter data, specified as a vector, a 2-D array or a 3-D array. The length of the data values must equal the length of the frequency values freq.

`s` — N-port S-parameters
`sparameters` object

N-port S-parameters, specified as a sparameters object.

`filename` — Network data file name
character vector

Network data file name, specified as a character vector. The data file must have .snp file extension (a Touchstone file).

`tol` — Relative error tolerance
`-40` (default) | scalar

Relative error tolerance, specified as a scalar less than or equal to 0 dB.

Note

Do not specify the tol input argument and Tolerance name-value argument when specifying number of poles of the fit using the NumPoles property.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: TendsToZero = true | 'TendsToZero',true

`Tolerance` — Relative error tolerance
`-40` (default) | scalar

Relative error tolerance, specified as a scalar less than or equal to 0 dB.

Note

Do not specify the tol input argument and Tolerance name-value argument when specifying number of poles of the fit using the NumPoles property.

Example: Tolerance=-30

Data Types: double

`TendsToZero` — Behavior of fit for large S-parameters
`true or 1` (default) | `false or 0`

Behavior of fit for large S-parameters, specified as 1 (true) or 0 (false). When true, the direct term in the fit is set to zero so that the rational fit F(S) tends to zero as S approaches infinity. When false, a nonzero direct term is allowed.

Example: TendsToZero=true

Data Types: logical

`MaxPoles` — Maximum number of poles
`1000` (default) | scalar nonnegative integer

Maximum number of poles, specified as a scalar nonnegative integer.

Example: MaxPoles=1002

Data Types: double

`ErrorMetric` — Error metrics in `rational` object
`'default'` (default) | `'Relative'`

Error metrics in the rational object, specified as one of the following:

If you specify 'ErrorMetric' as 'default', the rational object distributes the error evenly.
If you specify 'ErrorMetric' as 'Relative', the rational object fits both peaks and valleys or gets smaller error for smaller values.

Example: ErrorMetric='Relative'

Data Types: char

`NoiseFloor` — Ignores low-level noise in data
`-inf` (default) | scalar

Ignores low-level noise in the data, specified as a scalar.

Example: NoiseFloor=-60

Data Types: double

`Causal` — Pole stability
`true or 1` (default) | `false or 0`

Pole stability, specified as a logical true (1) or false (0). When you specify true, all the poles of the fit are stable. When you specify false,the poles can be anywhere in the complex plane.

Example: Causal=false

`Qlimit` — Maximum value of quality factor
`1000` (default) | positive scalar

Maximum value of the quality factor of the poles of the fit, specified as a positive scalar.

Example: Qlimit=1100

Data Types: double

`ColumnReduce` — Data reduction
`true or 1` (default) | `false or 0` | logical

Data reduction, specified as a logical 1 (true) or 0 (false). When you specify true, the function reduces the data for the fitter to save memory and computation time. Reduce data for the fitter in order to save memory and computation time, specified as a logical true or false.

Example: ColumnReduce=false

`PoleSharing` — Type of pole sharing
`All` (default) | `Column` | `Individual`

Since R2024a

Type of pole sharing to share the poles of the S-parameters, specified as one of the following:

All — Share all the poles of the S-parameters.
Column — Share the poles by S-parameter column terms.
Individual — Share the poles individually by S-parameter terms.

Data Types: char | string

`Display` — Display options for fitting algorithm
`'off'` (default) | `'on'` | `'plot'` | `'both'`

Display options for the fitting algorithm of the rational object, specified as one of the following:

'off'— No display
'on'— Printed information
'plot'— Plots of the interpolation progress
'both'— Both printed information and plots.

Example: Display='on'

Data Types: char

Properties

expand all

`NumPorts` — Number of ports
scalar integer

This property is read-only.

Number of ports in the original S-parameter data, returned as a scalar integer. The value of the NumPorts is determined from the S-parameter data.

`NumPoles` — Number of poles
nonegative integer

Number of poles in the fit, specified as a nonegative integer (since R2023a). If you do not specify the NumPoles property, then the object sets the property automatically.

Note

Do not specify the tol input argument and Tolerance name-value argument when specifying number of poles of the fit using the NumPoles property.

Example: 10

`Poles` — Poles of fit
row vector

Poles of the fit (A), specified as a row vector of length NumPoles-by-1. When you specify this property, the object sets the Residues, DirectTerm, and ErrDB properties or you can set them separately (since R2023a).

If you do not specify the Poles property, then the object sets the property automatically.

Note

When setting the poles of the fit using the Poles property, the NoiseFloor, Causal, ColumnReduce, MaxPoles, NumPoles, and Qlimit arguments are ignored.

Example: [-5.4e+10 + 4.7e+10i;-5.4e+10 - 4.7e+10i] specifies poles for a two-pole fit

Data Types: double

`Residues` — Residues in fit
3-D matrix

Residues in the fit or complex values of C in the equation provided in the description, specified as a 3-D matrix. The first two dimension of Residues must be of the same length as the first two dimension of data and the last dimension of Residues must be of the same length as Poles. If you specify this property, the object sets the DirectTerm and ErrDB properties or you can set them separately (since R2023a).

If you do not specify the Residues property, then the object sets the property automatically as a 3-D matrix of length NumPorts-by-NumPorts-by-NumPoles.

Data Types: double

`DirectTerm` — Direct term in fit
2-D matrix

Direct term in the fit or the value of D in the equation provided in the description, specified as a 2-D matrix. The length of this matrix must be the same as the first two dimensions of the data. If you specify this property, the object sets the ErrDB property (since R2023a).

Note

You must specify this argument with Poles and Residues.

If you do not specify this property, then the object sets the property automatically as a 2-D matrix of length NumPorts-by-NumPorts.

Example: [0 0;0 0]

Data Types: double

`ErrDB` — Error between fit and original data
scalar

This property is read-only.

Error between the fit and the original data, returned as a scalar in dB.

Object Functions

`timeresp`	Time response for rational objects
`stepresp`	Step-signal response for rational object and `rationalfit` function object
`freqresp`	Frequency response of rational object and `rationalfit` function object
`pwlresp`	Calculate time response of piecewise linear input signal
`impulse`	Impulse response for rational function object
`ispassive`	Return true if rational fit output is passive at all frequencies
`makepassive`	Enforce passivity of rational fit
`passivity`	Plot passivity of N-by-N rational fit output
`generateSPICE`	Generate SPICE file from `rationalfit` of S-parameters
`abcd`	Construct state-space matrices from `rational` object
`zpk`	Compute zeros, poles, and gain of rational object

Examples

collapse all

Fit `passive.s2p` File

Open Live Script

Create S-Parameters from the file named passive.s2p.

S = sparameters('passive.s2p');

Perform rational fitting of the S-parameters.

fit = rational(S);

Zeros, Poles, Gain, and DC Gain of Fit

Open Live Script

Create an S-Parameters object from the file named default.s2p. Perform rational fitting of the S-Parameters.

S = sparameters('default.s2p');
fit = rational(S,Display='plot')

Figure contains an axes object. The axes object with title Real part of data and response, xlabel Frequency (Hz), ylabel Data and response contains 12 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Response, Matched Points.

Figure contains an axes object. The axes object with title Imaginary part of data and response, xlabel Frequency (Hz), ylabel Data and response contains 12 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Response, Matched Points.

Figure contains an axes object. The axes object with title Error (difference between data and response), xlabel Frequency (Hz), ylabel Error contains 4 objects of type line. This object represents Error.

fit = 
  rational with properties:

      NumPorts: 2
      NumPoles: 52
         Poles: [52x1 double]
      Residues: [2x2x52 double]
    DirectTerm: [2x2 double]
         ErrDB: -22.6872

Calculate the zeros, poles, gain, and DC gain of the rational object.

[z,p,k,dcgain] = zpk(fit)

z=2×2 cell array
    {51x1 double}    {51x1 double}
    {51x1 double}    {51x1 double}

p=2×2 cell array
    {52x1 double}    {52x1 double}
    {52x1 double}    {52x1 double}

k = 2×2
10¹⁰ ×

    1.0544   -0.0194
    0.9158    0.0377

dcgain = 2×2

    0.1289   -0.0838
   -0.1209    0.7649

Fit Peaks and Valleys in `rational` Object

Open Live Script

Create an S-parameters object from the specified S2P file.

S = sparameters('sawfilterpassive.s2p');
f = S.Frequencies;

Create a rational object with the tolerance of -40 dB.

fit = rational(S,Tolerance=-40);

Compare the fit to the data. You can see the deviations at the smaller values on a semi-log plot.

dresp = freqresp(fit,f);
plot(f,20*log10(abs(squeeze(S.Parameters(2,1,:)))),...
    f,20*log10(abs(squeeze(dresp(2,1,:)))),f,20*log10(abs(squeeze(S.Parameters(2,1,:)-dresp(2,1,:)))))
title('Default Fitting for sawfilterpassive.s2p');
ylabel('dB');
xlabel('Frequency (Hz)');
legend('Data','Fit','Error','Location','northwest');

Figure contains an axes object. The axes object with title Default Fitting for sawfilterpassive.s2p, xlabel Frequency (Hz), ylabel dB contains 3 objects of type line. These objects represent Data, Fit, Error.

Create a rational object with 'ErrorMetric' set to 'Relative' to fit both peaks and valleys.

rfit = rational(S,Tolerance=-40,ErrorMetric='Relative');

Compare the fit to the data. The peaks and valleys are fitted.

rresp = freqresp(rfit,f);
figure(2)
plot(f,20*log10(abs(squeeze(S.Parameters(2,1,:)))),...
    f,20*log10(abs(squeeze(rresp(2,1,:)))), f, 20*log10(abs(squeeze(S.Parameters(2,1,:)-rresp(2,1,:)))));
title('Relative Error Fitting for sawfilterpassive.s2p');
ylabel('dB');
xlabel('Frequency (Hz)');
legend('Data','Fit','Error','Location','northwest');

Figure contains an axes object. The axes object with title Relative Error Fitting for sawfilterpassive.s2p, xlabel Frequency (Hz), ylabel dB contains 3 objects of type line. These objects represent Data, Fit, Error.

Ignore Low-Level Noise in Fitter Data

Open Live Script

Configure the S-parameter file reader for Touchstone 2.0 files to parses comments in the Touchstone 2.0 file and outputs errors if it detects if invalid characters in the comments of the Touchstone file.

setTouchstoneReader('ParseComments',true)

Create an S-parameters object from the specified S2P file.

S = sparameters('passive.s2p');
f = S.Frequencies;
data = S.Parameters;

Set one of the data entries to zero.

data(2,2,:) = 0;

Create a rational object with the tolerance of -40 dB.

fit = rational(f,data,Tolerance=-40);

Compare the fit to the data. The fit and the data match closely.

xresp = freqresp(fit,f);
figure(3)
plot(f,abs(squeeze(data(2,1,:))),f,abs(squeeze(xresp(2,1,:))))

Figure contains an axes object. The axes object contains 2 objects of type line.

Add noise to the data and create a rational object.

rng(1);
noisyData = data + 1e-4 * rand(size(S.Parameters));
nfit = rational(f,noisyData,Tolerance=-40);

Compare the fit to the data with noise. Noise cannot be fitted because this is a data with a higher order fit with a worse error metric.

nresp = freqresp(nfit,f);
figure(4)
plot(f,abs(squeeze(noisyData(2,2,:))),f,abs(squeeze(nresp(2,2,:))))

Figure contains an axes object. The axes object contains 2 objects of type line.

Create a rational object with the noise floor of -60 dB and plot the fit. The fitter ignores low-level noise.

ffit = rational(f,noisyData,Tolerance=-40,NoiseFloor=-60);
fresp = freqresp(ffit,f);
figure(5)
plot(f,abs(squeeze(noisyData(2,2,:))),f,abs(squeeze(fresp(2,2,:))))

Figure contains an axes object. The axes object contains 2 objects of type line.

Control Poles in Rational Object

Since R2023a

Open Live Script

Create an S-parameter object.

S = sparameters('passive.s2p');

Perform a default fit.

fit = rational(S)

fit = 
  rational with properties:

      NumPorts: 2
      NumPoles: 8
         Poles: [8x1 double]
      Residues: [2x2x8 double]
    DirectTerm: [2x2 double]
         ErrDB: -40.4597

Limit the number of poles to four, and note that and that the error in fit1 is higher than the error in fit.

fit1 = rational(S,NumPoles=4)

fit1 = 
  rational with properties:

      NumPorts: 2
      NumPoles: 4
         Poles: [4x1 double]
      Residues: [2x2x4 double]
    DirectTerm: [2x2 double]
         ErrDB: -29.1219

Force the rational object to use twice the number of poles in fit. Note that the error in fit2 is lower than fit.

fit2 = rational(S,NumPoles=2*fit.NumPoles)

fit2 = 
  rational with properties:

      NumPorts: 2
      NumPoles: 16
         Poles: [16x1 double]
      Residues: [2x2x16 double]
    DirectTerm: [2x2 double]
         ErrDB: -42.4669

References

[1] Nakatsukasa, Yuji, Olivier Sète, and Lloyd N. Trefethen. “The AAA Algorithm for Rational Approximation.” SIAM Journal on Scientific Computing 40, no. 3 (January 2018): A1494–1522. https://doi.org/10.1137/16M1106122.

Version History

Introduced in R2020a

expand all

R2024a: Share poles of S-parameters using `rational` object

You can now use the new PoleSharing name-value argument of the rational object to share all poles of the S-parameters or share the poles individually by S-parameter terms, or by S-parameter column terms. The rational object by default shares all poles of the S-parameters.

R2023b: Recommended over `rationalfit`

rational is recommend over rationalfit because it enables faster simulation and improved fitting of complex frequency-dependent data.

R2023a: Specify poles and residues in `rational` object

The rational object now allow you to specify:

Number of poles
Poles
Residues
Direct term

rational

Description

Creation

Syntax

Description

Input Arguments

freq — Nonnegative frequencies vector

data — Network parameter data vector | 2-D array | 3-D array

s — N-port S-parameters sparameters object

filename — Network data file name character vector

tol — Relative error tolerance -40 (default) | scalar

Tolerance — Relative error tolerance -40 (default) | scalar

TendsToZero — Behavior of fit for large S-parameters true or 1 (default) | false or 0

MaxPoles — Maximum number of poles 1000 (default) | scalar nonnegative integer

ErrorMetric — Error metrics in rational object 'default' (default) | 'Relative'

NoiseFloor — Ignores low-level noise in data -inf (default) | scalar

Causal — Pole stability true or 1 (default) | false or 0

Qlimit — Maximum value of quality factor 1000 (default) | positive scalar

ColumnReduce — Data reduction true or 1 (default) | false or 0 | logical

PoleSharing — Type of pole sharing All (default) | Column | Individual

Display — Display options for fitting algorithm 'off' (default) | 'on' | 'plot' | 'both'

Properties

NumPorts — Number of ports scalar integer

NumPoles — Number of poles nonegative integer

Poles — Poles of fit row vector

Residues — Residues in fit 3-D matrix

DirectTerm — Direct term in fit 2-D matrix

ErrDB — Error between fit and original data scalar

Object Functions

Examples

Fit passive.s2p File

Zeros, Poles, Gain, and DC Gain of Fit

Fit Peaks and Valleys in rational Object

Ignore Low-Level Noise in Fitter Data

Control Poles in Rational Object

References

Version History

R2024a: Share poles of S-parameters using rational object

R2023b: Recommended over rationalfit

R2023a: Specify poles and residues in rational object

See Also

`freq` — Nonnegative frequencies
vector

`data` — Network parameter data
vector | 2-D array | 3-D array

`s` — N-port S-parameters
`sparameters` object

`filename` — Network data file name
character vector

`tol` — Relative error tolerance
`-40` (default) | scalar

`Tolerance` — Relative error tolerance
`-40` (default) | scalar

`TendsToZero` — Behavior of fit for large S-parameters
`true or 1` (default) | `false or 0`

`MaxPoles` — Maximum number of poles
`1000` (default) | scalar nonnegative integer

`ErrorMetric` — Error metrics in `rational` object
`'default'` (default) | `'Relative'`

`NoiseFloor` — Ignores low-level noise in data
`-inf` (default) | scalar

`Causal` — Pole stability
`true or 1` (default) | `false or 0`

`Qlimit` — Maximum value of quality factor
`1000` (default) | positive scalar

`ColumnReduce` — Data reduction
`true or 1` (default) | `false or 0` | logical

`PoleSharing` — Type of pole sharing
`All` (default) | `Column` | `Individual`

`Display` — Display options for fitting algorithm
`'off'` (default) | `'on'` | `'plot'` | `'both'`

`NumPorts` — Number of ports
scalar integer

`NumPoles` — Number of poles
nonegative integer

`Poles` — Poles of fit
row vector

`Residues` — Residues in fit
3-D matrix

`DirectTerm` — Direct term in fit
2-D matrix

`ErrDB` — Error between fit and original data
scalar

Fit `passive.s2p` File

Fit Peaks and Valleys in `rational` Object

R2024a: Share poles of S-parameters using `rational` object

R2023b: Recommended over `rationalfit`

R2023a: Specify poles and residues in `rational` object