Build Manipulator Robot Using Kinematic DH Parameters
Use the Denavit-Hartenberg (DH) parameters of the Puma560® manipulator robot to incrementally build a rigid body tree robot model. Specify the relative DH parameters for each joint as you attach them. Visualize the robot frames, and interact with the final model.
The DH parameters define the geometry of how each rigid body attaches to its parent via a joint. The parameters follow a four transformation convention:
— Length of the common normal line between the two z-axes, which is perpendicular to both axes
— Angle of rotation for the common normal
— Offset along the z-axis in the normal direction, from parent to child
— Angle of rotation for the x-axis along the previous z-axis
Specify the parameters for the Puma560 robot [1] as a matrix.
dhparams = [0 pi/2 0 0;
0.4318 0 0 0
0.0203 -pi/2 0.15005 0;
0 pi/2 0.4318 0;
0 -pi/2 0 0;
0 0 0 0];Create a rigid body tree object.
robot = rigidBodyTree;
Create a cell array for the rigid body object, and another for the joint objects. Iterate through the DH parameters performing this process:
Create a
rigidBodyobject with a unique name.Create and name a revolute
rigidBodyJointobject.Use
setFixedTransformto specify the body-to-body transformation of the joint using DH parameters. The function ignores the final element of the DH parameters,theta, because the angle of the body is dependent on the joint position.Use
addBodyto attach the body to the rigid body tree.
bodies = cell(6,1); joints = cell(6,1); for i = 1:6 bodies{i} = rigidBody(['body' num2str(i)]); joints{i} = rigidBodyJoint(['jnt' num2str(i)],"revolute"); setFixedTransform(joints{i},dhparams(i,:),"dh"); bodies{i}.Joint = joints{i}; if i == 1 % Add first body to base addBody(robot,bodies{i},"base") else % Add current body to previous body by name addBody(robot,bodies{i},bodies{i-1}.Name) end end
Verify that your robot has been built properly by using the showdetails or show function. The showdetails function lists all the bodies of the robot in the MATLAB® command window. The show function displays the robot with a specified configuration (home by default).
showdetails(robot)
-------------------- Robot: (6 bodies) Idx Body Name Joint Name Joint Type Parent Name(Idx) Children Name(s) --- --------- ---------- ---------- ---------------- ---------------- 1 body1 jnt1 revolute base(0) body2(2) 2 body2 jnt2 revolute body1(1) body3(3) 3 body3 jnt3 revolute body2(2) body4(4) 4 body4 jnt4 revolute body3(3) body5(5) 5 body5 jnt5 revolute body4(4) body6(6) 6 body6 jnt6 revolute body5(5) --------------------
figure(Name="PUMA Robot Model")
show(robot);
Interact with Robot Model
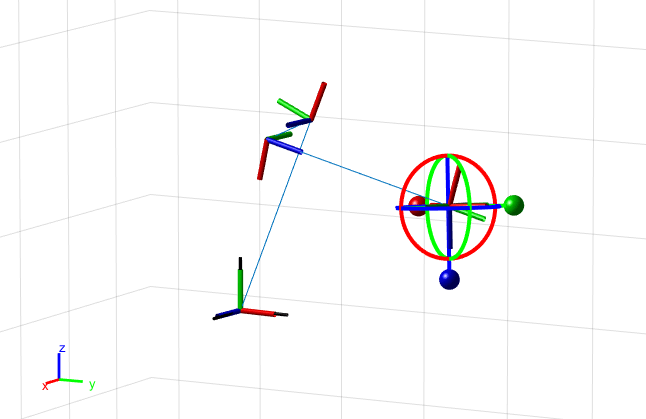
Visualize the robot model to confirm its dimensions by using the interactiveRigidBodyTree object.
figure(Name="Interactive GUI")
gui = interactiveRigidBodyTree(robot,MarkerScaleFactor=0.5);
Click and drag the marker in the interactive GUI to reposition the end effector. The GUI uses inverse kinematics to solve for the joint positions that achieve the best possible match to the specified end-effector position. Right-click a specific body frame to set it as the target marker body, or to change the control method for setting specific joint positions.
Next Steps
Now that you have built your model in MATLAB®, these are some possible next steps.
Perform Inverse Kinematics to get joint configurations based on desired end-effector positions. Specify robot constraints in addition to those of the model parameters, including aiming constraints, Cartesian bounds, and pose targets.
Trajectory Generation, based on waypoints and other parameters, with trapezoidal velocity profiles, B-splines, or polynomial trajectories.
Perform Manipulator Planning utilizing your robot models and a rapidly-exploring random tree (RRT) path planner.
Use Collision Detection with obstacles in your environment to ensure safe and effective motion for your robot.
References
[1] Corke, P. I., and B. Armstrong-Helouvry. “A Search for Consensus Among Model Parameters Reported for the PUMA 560 Robot.” Proceedings of the 1994 IEEE International Conference on Robotics and Automation, 1608–13. San Diego, CA, USA: IEEE Computer Soc. Press, 1994. https://doi.org/10.1109/ROBOT.1994.351360.