mixsyn

Mixed-sensitivity H_∞ synthesis method for robust control loop-shaping design

collapse all in page

Syntax

[K,CL,gamma,info] = mixsyn(G,W1,W2,W3)

[K,CL,gamma] = mixsyn(G,W1,W2,W3,gamTry)

[K,CL,gamma] = mixsyn(G,W1,W2,W3,gamRange)

[K,CL,gamma] = mixsyn(___,opts)

[K,CL,gamma,info] = mixsyn(___)

Description

[K,CL,gamma,info] = mixsyn(G,W1,W2,W3) computes a controller that minimizes the H_∞ norm of the weighted closed-loop transfer function

$M (s) = [\begin{matrix} W_{1} S \\ W_{2} K S \\ W_{3} T \end{matrix}],$

where S = (I + GK)^–1 and T = (I – S) is the complementary sensitivity of the following control system.

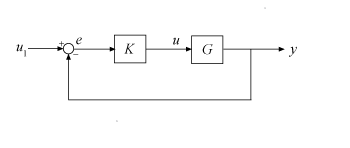
Block diagram of G*K with unit negative feedback, that is, feedback(G*K,eye(N)) where N is the number of outputs of G

You choose the weighting functions W1,W2,W3 to shape the frequency responses for tracking and disturbance rejection, controller effort, and noise reduction and robustness, respectively. For details about how to choose weighting functions, see Mixed-Sensitivity Loop Shaping.

mixsyn computes the controller K that yields the minimum ||M(s)||_∞, which is returned as gamma. For the returned controller K,

$\begin{matrix} {‖ S ‖}_{\infty} \leq γ | W_{1}^{- 1} | \\ {‖ K S ‖}_{\infty} \leq γ | W_{2}^{- 1} | \\ {‖ T ‖}_{\infty} \leq γ | W_{3}^{- 1} | . \end{matrix}$

example

[K,CL,gamma] = mixsyn(G,W1,W2,W3,gamTry) calculates a controller for the target performance level gamTry. Specifying gamTry can be useful when the optimal controller performance is better than you need for your application. In that case, a less-than-optimal controller can have smaller gains and be better conditioned numerically. When W1,W2,W3 capture the desired limits on the gains of S, KS, and T, use gamtry = 1 to just enforce those limits.

If gamTry is not achievable, mixsyn returns [] for K and CL, and Inf for gamma.

[K,CL,gamma] = mixsyn(G,W1,W2,W3,gamRange) searches the range gamRange for the best achievable performance. Specify the range with a vector of the form [gmin,gmax]. Limiting the search range can speed up computation by reducing the number of iterations performed by mixsyn to test different performance levels.

[K,CL,gamma] = mixsyn(___,opts) specifies additional computation options. To create opts, use hinfsynOptions. Specify opts after all other input arguments.

[K,CL,gamma,info] = mixsyn(___) returns a structure containing additional information about the H_∞ synthesis computation. You can use this argument with any of the previous syntaxes.

Examples

collapse all

Loop Shaping with mixsyn

Open Live Script

Use mixsyn for sensitivity and complementary sensitivity loop shaping. Create a plant model and weighting functions that:

Shape the sensitivity function for reference tracking and disturbance rejection (W1 = 1/S large inside the control bandwidth).
Shape the complementary sensitivity for robustness and noise attenuation (W3 = 1/T large outside the control bandwidth).
Limit the control effort (W2 = 1/KS large inside the control bandwidth).

(For more information about choosing weighting functions, see Mixed-Sensitivity Loop Shaping.)

s = zpk('s');
G = (s-1)/(s+1)^2;

W1 = makeweight(10,[1 0.1],0.01);
W2 = makeweight(0.1,[32 0.32],1);
W3 = makeweight(0.01,[1 0.1],10);

bodemag(W1,W2,W3)

MATLAB figure

Design the controller.

[K,CL,gamma] = mixsyn(G,W1,W2,W3);

mixsyn shapes the singular values of the sensitivity function S, the complementary sensitivity function T, and the control effort R = K*S. Examine the results of the synthesis and the shapes of these transfer functions.

S = feedback(1,G*K);
KS = K*S;
T = 1-S;
sigma(S,'b',KS,'r',T,'g',gamma/W1,'b-.',ss(gamma/W2),'r-.',gamma/W3,'g-.',{1e-3,1e3})
legend('S','KS','T','GAM/W1','GAM/W2','GAM/W3','Location','SouthWest')
grid

MATLAB figure

Input Arguments

collapse all

`G` — Plant
dynamic system model

Plant, specified as a dynamic system model such as a state-space (ss) model. G can be any LTI model. mixsyn assumes the following control structure.

Block diagram of G*K with unit negative feedback, that is, feedback(G*K,eye(N)) where N is the number of outputs of G

If G is a generalized state-space model with uncertain or tunable control design blocks, then mixsyn uses the nominal or current value of those elements.

`W1,W2,W3` — Weighting functions
dynamic system model | `[]`

Weighting functions, specified as dynamic system models. Choose the weighting functions W1,W2,W3 to shape the frequency responses for tracking and disturbance rejection, controller effort, and noise reduction and robustness. Typically:

For good reference-tracking and disturbance-rejection performance, choose W1 large inside the control bandwidth to obtain small S.
For robustness and noise attenuation, choose W3 large outside the control bandwidth to obtain small T.
To limit control effort in a particular frequency band, increase the magnitude of W₂ in this frequency band to obtain small KS.

If one of the weights is not needed, set it to []. For instance, if you do not want to restrict control effort, use W2 = [].

Use makeweight to create weighting functions with the desired gain profiles. For details about choosing weighting functions, see Mixed-Sensitivity Loop Shaping.

If G has N_U inputs and N_Y outputs, then W1,W2,W3 must be either SISO or square systems of size N_Y, N_U, and N_Y, respectively.

Because S + T = I, mixsyn cannot make both S and T small (less than 0 dB) in the same frequency range. Therefore, when you specify weights for loop shaping, there must be a frequency band in which both W1 and W3 are below 0 dB.

`gamTry` — Target performance level
positive scalar

Target performance level, specified as a positive scalar. mixsyn attempts to compute a controller such that the H_∞ of the weighted closed-loop system M(s) does not exceed gamTry. If this performance level is achievable, then the returned controller has gamma ≤ gamTry. If gamTry is not achievable, mixsyn returns an empty controller.

`gamRange` — Performance range for search
`[0,Inf]` (default) | vector of form `[gmin,gmax]`

Performance range for search, specified as a vector of the form [gmin,gmax]. The mixsyn command tests only performance levels within that range. It returns a controller with performance:

gamma ≤ gmin, when gmin is achievable.
gmin < gamma < gmax, when gmax is achievable and but gmin is not.
gamma = Inf when gmax is not achievable. In this case, mixsyn returns [] for K and CL.

If you know a range of feasible performance levels, specifying this range can speed up computation by reducing the number of iterations performed by mixsyn to test different performance levels.

`opts` — Options
`hinfsynOptions` object

Additional options for the computation, specified as an options object you create using hinfsynOptions.

Use opts to specify options for the underlying hinfsyn computation (see Algorithms). Available options include:

Display algorithm progress at the command line.
Turn off automatic scaling and regularization.
Specify an optimization method.

For information about all options, see hinfsynOptions.

Output Arguments

collapse all

`K` — Controller
`ss` model object | `[]`

Controller, returned as a state-space (ss) model object or [].

If you supply gamTry or gamRange and the specified performance values are not achievable, then K = [].

`CL` — Augmented closed-loop transfer function
`ss` model object | `[]`

Augmented closed-loop transfer function, returned as a state-space (ss) model object or []. The augmented closed-loop transfer function is given by

$M (s) = [\begin{matrix} W_{1} S \\ W_{2} K S \\ W_{3} T \end{matrix}],$

where S = (I + GK)^–1 and T = (I – S) is the complementary sensitivity of the unweighted control system. See Mixed-Sensitivity Loop Shaping.

The returned performance level gamma is the H_∞ norm of CL.

If you supply gamTry or gamRange and the specified performance levels are not achievable, then CL = [].

`gamma` — Controller performance
nonnegative scalar | `Inf`

Controller performance, returned as a nonnegative scalar value or Inf. This value is the performance achieved using the returned controller K, and is the H_∞ norm of CL (see hinfnorm). If you do not provide performance levels to test using gamTry or gamRange, then gamma is the best achievable performance level.

If you provide gamTry or gamRange, then gamma is the actual performance level achieved by the controller computed for the best passing performance level that hinfsyn tries. If the specified performance levels are not achievable, then gamma = Inf.

`info` — Synthesis data
structure | `[]`

Additional synthesis data, returned as a structure or [] (if the specified performance level is not achievable). info contains data about the underlying hinfsyn computation used by mixsyn to minimize the H_∞ norm of the closed-loop transfer function M(s). For details about the meaning of the fields of info, see the info output argument of hinfsyn.

Algorithms

mixsyn uses your weighting functions to generate an augmented plant P = augw(G,W1,W2,W3). It then invokes hinfsyn to find a controller that minimizes the H_∞ norm of the closed-loop transfer function M(s) = LFT(P,K). For details, see Mixed-Sensitivity Loop Shaping.

Version History

Introduced before R2006a

expand all

R2019b: Name,Value options are not recommended

As of R2019b, using Name,Value syntax to specify options for mixsyn is not recommended. Instead, to set a target performance range, use the gamRange input argument. For other options, create an options set with hinfsynOptions.

The following table shows how to update your calls to mixsyn to use the recommended ways of specifying options.

Not Recommended	Recommended
`[K,CL,GAM] = mixsyn(___,'GMIN',gmin,'GMAX',gmax)`	gamRange = [gmin gmax]; [K,CL,GAM] = mixsyn(___,gamRange)
`[K,CL,GAM] = mixsyn(___,'TOLGAM',tol)`	opts = hinfsynOptions('RelTol',tol); [K,CL,GAM] = mixsyn(___,opts);
`[K,CL,GAM] = mixsyn(___,'METHOD',meth)`	opts = hinfsynOptions('Method',meth); [K,CL,GAM] = mixsyn(___,opts);
`[K,CL,GAM] = mixsyn(___,'DISPLAY','on')`	opts = hinfsynOptions('Display','on'); [K,CL,GAM] = mixsyn(___,opts);

For more information about these and additional options available for mixsyn computations, see hinfsynOptions.

R2019b: `info` output argument changed

The fields of the optional output argument info changed in R2019b. The new fields of info are the same as those of hinfsyn. For more information about the change, see info output argument changed on the hinfsyn reference page, which describes the same change for hinfsyn in R2018b.

mixsyn

Syntax

Description

Examples

Loop Shaping with mixsyn

Input Arguments

`G` — Plant
dynamic system model

`W1,W2,W3` — Weighting functions
dynamic system model | `[]`

`gamTry` — Target performance level
positive scalar

`gamRange` — Performance range for search
`[0,Inf]` (default) | vector of form `[gmin,gmax]`

`opts` — Options
`hinfsynOptions` object

Output Arguments

`K` — Controller
`ss` model object | `[]`

`CL` — Augmented closed-loop transfer function
`ss` model object | `[]`

`gamma` — Controller performance
nonnegative scalar | `Inf`

`info` — Synthesis data
structure | `[]`

Algorithms

Version History

R2019b: Name,Value options are not recommended

R2019b: `info` output argument changed

See Also

Topics

mixsyn

Syntax

Description

Examples

Loop Shaping with mixsyn

Input Arguments

G — Plant dynamic system model

W1,W2,W3 — Weighting functions dynamic system model | []

gamTry — Target performance level positive scalar

gamRange — Performance range for search [0,Inf] (default) | vector of form [gmin,gmax]

opts — Options hinfsynOptions object

Output Arguments

K — Controller ss model object | []

CL — Augmented closed-loop transfer function ss model object | []

gamma — Controller performance nonnegative scalar | Inf

info — Synthesis data structure | []

Algorithms

Version History

R2019b: Name,Value options are not recommended

R2019b: info output argument changed

See Also

Topics

`G` — Plant
dynamic system model

`W1,W2,W3` — Weighting functions
dynamic system model | `[]`

`gamTry` — Target performance level
positive scalar

`gamRange` — Performance range for search
`[0,Inf]` (default) | vector of form `[gmin,gmax]`

`opts` — Options
`hinfsynOptions` object

`K` — Controller
`ss` model object | `[]`

`CL` — Augmented closed-loop transfer function
`ss` model object | `[]`

`gamma` — Controller performance
nonnegative scalar | `Inf`

`info` — Synthesis data
structure | `[]`

R2019b: `info` output argument changed