hinfsyn
Compute H-infinity optimal controller
Syntax
Description
[
computes a stabilizing H∞-optimal controller
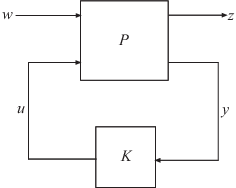
K,CL,gamma] = hinfsyn(P,nmeas,ncont)K for the plant P. The plant has a partitioned
form
where:
w represents the disturbance inputs.
u represents the control inputs.
z represents the error outputs to be kept small.
y represents the measurement outputs provided to the controller.
nmeas and ncont are the number of signals in
y and u, respectively. y and
u are the last outputs and inputs of P,
respectively. hinfsyn returns a controller K that
stabilizes P and has the same number of states. The closed-loop system
CL = lft(P,K) achieves the performance level
gamma, which is the H∞ norm
of CL (see hinfnorm).
[
calculates a controller for the target performance level K,CL,gamma] = hinfsyn(P,nmeas,ncont,gamTry)gamTry.
Specifying gamTry can be useful when the optimal controller performance
is better than you need for your application. In that case, a less-than-optimal controller
can have smaller gains and be more numerically well-conditioned. If
gamTry is not achievable, hinfsyn returns
[] for K and CL, and
Inf for gamma.
[
searches the range K,CL,gamma] = hinfsyn(P,nmeas,ncont,gamRange)gamRange for the best achievable performance.
Specify the range with a vector of the form [gmin,gmax]. Limiting the
search range can speed up computation by reducing the number of iterations performed by
hinfsyn to test different performance levels.
[
specifies additional computation options. To create K,CL,gamma] = hinfsyn(___,opts)opts, use hinfsynOptions.
Specify opts after all other input arguments.
Examples
Input Arguments
Output Arguments
More About
Tips
hinfsyngives you state-feedback gains and observer gains that you can use to express the controller in observer form. The observer form of the controllerKis:Here, we is an estimate of the worst-case perturbation and the innovation term e is given by:
hinfsynreturns the state-feedback gains Ku and Kw and the observer gains Lx and Lu as fields in theinfooutput argument.You can use this form of the controller for gain scheduling in Simulink®. To do so, tabulate the plant matrices and the controller gain matrices as a function of the scheduling variables using the Matrix Interpolation (Simulink) block. Then, use the observer form of the controller to update the controller variables as the scheduling variables change.
Algorithms
By default, hinfsyn uses the two-Riccati formulae
([1],[2]) with loop shifting
[3]. You can use
hinfsynOptions to change to an LMI-based method
([4],[5],[6]). You can also
specify a maximum-entropy method. In that method, hinfsyn returns the
H∞ controller that maximizes an entropy
integral relating to the point S0. For continuous-time systems, this
integral is:
where is the closed-loop transfer function CL. A similar
integral is used for discrete-time systems.
For all methods, the function uses a standard γ-iteration technique to determine the optimal value of the performance level γ. γ-iteration is a bisection algorithm that starts with high and low estimates of γ and iterates on γ values to approach the optimal H∞ control design.
At each value of γ, the algorithm tests a γ value to
determine whether a solution exists. In the Riccati-based method, the algorithm computes the
smallest performance level for which the stabilizing Riccati solutions X =
X∞/γ and Y =
Y∞/γ exist. For any γ greater than that performance level and
in the range gamRange, the algorithm evaluates the central controller
formulas (K formulas) and checks the closed-loop stability of CL =
lft(P,K). This step is equivalent to verifying the conditions:
min(eig(X)) ≥ 0min(eig(Y)) ≥ 0rho(XY)< 1, where the spectral radiusrho(XY) = max(abs(eig(XY)))
A γ that meets these conditions passes. The
stopping criterion for the bisection algorithm requires the relative difference between the
last γ value that failed and the last γ value that
passed be less than 0.01. (You can change this criterion using
hinfsynOptions.) hinfsyn returns the controller
corresponding to the smallest tested γ value that passes. For discrete-time
controllers, the algorithm performs additional computations to construct the feedthrough
matrix DK.
Use the Display option of hinfsynOptions to make
hinfsyn display values showing which of the conditions are satisfied
for each γ value tested.
The algorithm works best when the following conditions are satisfied by the plant:
D12 and D21 have full rank.
has full column rank for all ω ∊ R.
has full row rank for all ω ∊ R.
When these rank conditions do not hold, the controller may have undesirable properties. If
D12 and
D21 are not full rank, then the
H∞ controller K might
have large high-frequency gain. If either of the latter two rank conditions does not hold at
some frequency ω, the controller might have very lightly damped poles near
that frequency.
References
[1] Glover, K., and J.C. Doyle. "State-space formulae for all stabilizing controllers that satisfy an H∞ norm bound and relations to risk sensitivity." Systems & Control Letters, Vol. 11, Number 8, 1988, pp. 167–172.
[2] Doyle, J.C., K. Glover, P. Khargonekar, and B. Francis. "State-space solutions to standard H2 and H∞ control problems." IEEE Transactions on Automatic Control, Vol 34, Number 8, August 1989, pp. 831–847.
[3] Safonov, M.G., D.J.N. Limebeer, and R.Y. Chiang. "Simplifying the H∞ Theory via Loop Shifting, Matrix Pencil and Descriptor Concepts." Int. J. Contr., Vol. 50, Number 6, 1989, pp. 2467-2488.
[4] Packard, A., K. Zhou, P. Pandey, J. Leonhardson, and G. Balas. "Optimal, constant I/O similarity scaling for full-information and state-feedback problems." Systems & Control Letters, Vol. 19, Number 4, 1992, pp. 271–280.
[5] Gahinet, P., and P. Apkarian. "A linear matrix inequality approach to H∞-control." Int. J. Robust and Nonlinear Control, Vol. 4, Number. 4, 1994, pp. 421–448.
[6] Iwasaki, T., and R.E. Skelton. "All controllers for the general H∞-control problem: LMI existence conditions and state space formulas." Automatica, Vol. 30, Number 8, 1994, pp. 1307–1317.