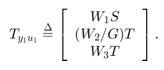h2syn
Compute H2 optimal controller
Syntax
Description
[
computes a stabilizing H2-optimal controller
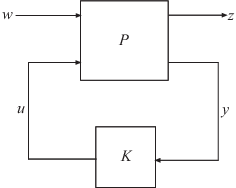
K,CL,gamma] = h2syn(P,nmeas,ncont)K for the plant P. The plant has a partitioned
form
where:
w represents the disturbance inputs.
u represents the control inputs.
z represents the error outputs to be kept small.
y represents the measurement outputs provided to the controller.
nmeas and ncont are the number of signals in
y and u, respectively. y and
u are the last outputs and inputs of P,
respectively. h2syn returns a controller K that
stabilizes P and has the same number of states. The closed-loop system
CL = lft(P,K) achieves the performance level
gamma, which is the H2 norm
of CL (see norm).
Examples
Input Arguments
Output Arguments
Tips
h2syngives you state-feedback gain and observer gains that you can use to express the controller in observer form. The observer form of the controllerKis:Here, the innovation term e is:
h2synreturns the state-feedback gain Ku and the observer gains Lx and Lu as fields in theinfooutput argument.You can use this form of the controller for gain scheduling in Simulink®. To do so, tabulate the plant matrices and the controller gain matrices as a function of the scheduling variables using the Matrix Interpolation (Simulink) block. Then, use the observer form of the controller to update the controller variables as the scheduling variables change.
Do not choose weighting functions with poles very close to s = 0 (z = 1 for discrete-time systems). For instance, although it might seem sensible to choose W = 1/s to enforce zero steady-state error, doing so introduces an unstable pole that cannot be stabilized, causing synthesis to fail. Instead, choose W = 1/(s + δ). The value δ must be small but not very small compared to system dynamics. For instance, for best numeric results, if your target crossover frequency is around 1 rad/s, choose δ = 0.0001 or 0.001. Similarly, in discrete time, choose sample times such that system and weighting dynamics are not more than a decade or two below the Nyquist frequency.
Algorithms
h2syn uses the methods described in Chapter 14 of [1].
References
[1] Zhou, K., Doyle, J., Glover, K, Robust and Optimal Control. Upper Saddle River, NJ: Prentice Hall, 1996.
Version History
Introduced before R2006a