kurtogram
Visualize spectral kurtosis
Syntax
Description
[
returns the fast kurtogram along with a set of parameters you can use for follow-on
bandpass filter design and spectral kurtosis:kgram,f,w,fc,wc,bw] = kurtogram(___)
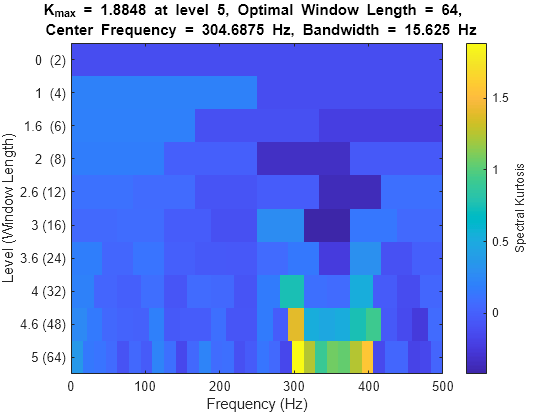
f— Frequency vector forkgramw— Window size vector forkgramfc— Frequency where the maximal spectral kurtosis is locatedwc— Window size where the maximal spectral kurtosis on the kurtogram is locatedbw— Suggested bandwidth for the optimal bandpass filter
You can use this syntax with any of the input arguments in previous syntaxes.
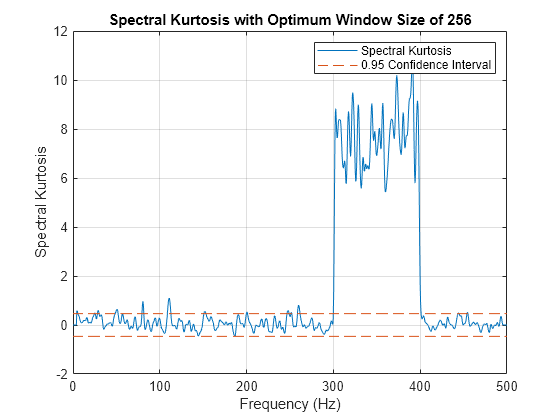
kurtogram(___) plots the kurtogram, along
with key critical optimization parameters, without returning any data. You can
use this syntax with any of the input arguments in previous syntaxes.
Examples
Input Arguments
Output Arguments
More About
References
[1] Antoni, J., and R. B. Randall. "Fast Computation of the Kurtogram for the Detection of Transient Faults." Mechanical Systems and Signal Processing. Vol. 20, Issue 1, 2007, pp. 108–124.