polyscale
Scale roots of polynomial
Syntax
Description
Examples
Input Arguments
Output Arguments
Tips
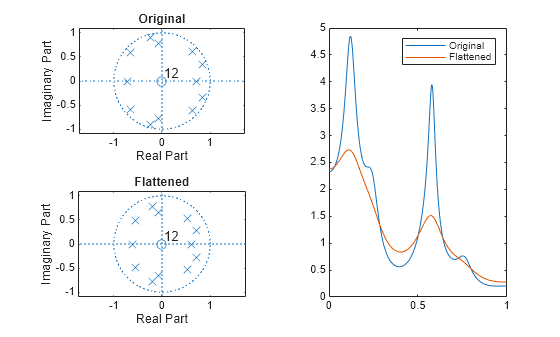
Reducing the radius of the roots in an autoregressive polynomial expands (flattens) the bandwidth of the spectral peaks in the frequency response. This operation is often referred to as bandwidth expansion.
Version History
Introduced before R2006a