sigwin.blackman Class

Namespace: sigwin

Construct Blackman window object

Description

Note

The use of sigwin.blackman is not recommended. Use blackman instead.

sigwin.blackman creates a handle to a Blackman window object for use in spectral analysis and FIR filtering by the window method. Object methods enable workspace import and ASCII file export of the window values.

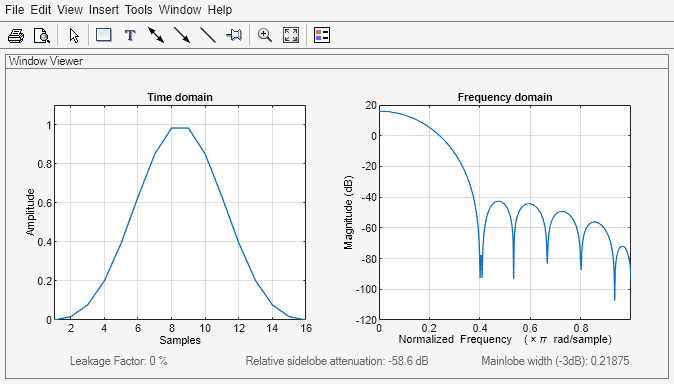
The following equation defines the Blackman window of length N:

$w (n) = 0.42 - 0.5 \cos (\frac{2 π n}{L - 1}) + 0.08 \cos (\frac{4 π n}{L - 1}), 0 \leq n \leq M - 1$

where M is N/2 for N even and (N+1)/2 for N odd.

In the symmetric case, the second half of the Blackman window $M \leq n \leq N - 1$ is obtained by flipping the first half around the midpoint. The symmetric option is the preferred method when using a Blackman window in FIR filter design.

The periodic Blackman window is constructed by extending the desired window length by one sample to N+1, constructing a symmetric window, and removing the last sample. The periodic version is the preferred method when using a Blackman window in spectral analysis because the discrete Fourier transform assumes periodic extension of the input vector.

Construction

H = sigwin.blackman returns a Blackman window object H of length 64 with symmetric sampling.

H = sigwin.blackman(Length) returns a Blackman window object H of length Length with symmetric sampling. Length requires a positive integer. Entering a positive noninteger value for Length rounds the length to the nearest integer. Entering a 1 for Length results in a window with a single value of 1.

H = sigwin.blackman(Length,SamplingFlag) returns a Blackman window object H with sampling Sampling_Flag. The Sampling_Flag can be either 'symmetric' or 'periodic'.

Properties

Length

Blackman window length. Must be a positive integer. Entering a positive noninteger value for Length rounds the length to the nearest integer. Entering a 1 for Length results in a window with a single value of 1.

SamplingFlag

'symmetric' is the default and forces exact symmetry between the first and second halves of the Blackman window. A symmetric window is preferred in FIR filter design by the window method.

'periodic' designs a symmetric Blackman window of length Length+1 and truncates the window to length Length. This design is preferred in spectral analysis where the window is treated as one period of a Length-point periodic sequence.

Methods

generate	Generates Blackman window
info	Display information about Blackman window object
winwrite	Save Blackman window in ASCII file

Copy Semantics

Handle. To learn how this affects your use of the class, see Copying Objects in the MATLAB^® Programming Fundamentals documentation.

Examples

collapse all

Blackman Window

Open Live Script

Generate a Blackman window of length N = 16. Return its values as a column vector. Show information about the window object. Display the window.

H = sigwin.blackman(16);

win = generate(H)

wininfo = info(H)

wininfo = 4x26 char array
    'Blackman Window           '
    '---------------           '
    'Length         : 16       '
    'Sampling Flag  : symmetric'

wvtool(H)

$Figure Window Visualization Tool contains 2 axes objects and other objects of type uimenu, uitoolbar, uipanel. Axes object 1 with title Time domain, xlabel Samples, ylabel Amplitude contains an object of type line. Axes object 2 with title Frequency domain, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Magnitude (dB) contains an object of type line.$

References

Oppenheim, Alan V., and Ronald W. Schafer. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1989.