Main Content

凯塞窗

凯塞窗近似于扁长椭圆形窗，它使主瓣能量与旁瓣能量之比最大。对于特定长度的凯塞窗，参数 β 控制相对旁瓣衰减。对于给定的 β，相对旁瓣衰减相对于窗长度是固定的。语句 kaiser (n,beta) 计算长度为 n、参数为 beta 的凯塞窗。

随着 β 的增加，相对旁瓣衰减降低，主瓣宽度增加。此屏幕截图显示，对于固定的 β 参数，当窗长度变化时，相对旁瓣衰减大致保持不变。

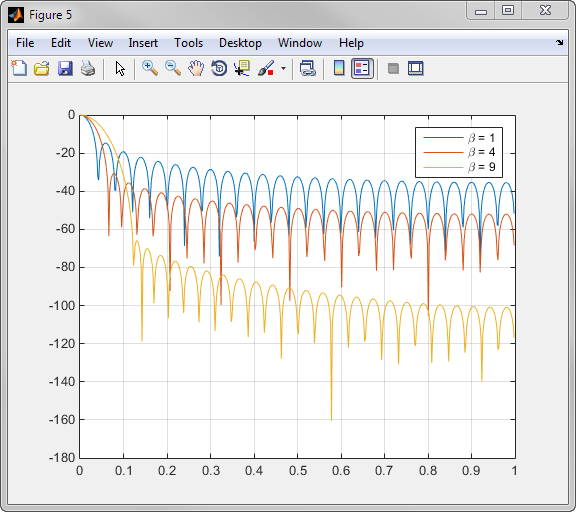
此示例显示了长度为 50、β 参数分别为 1、4 和 9 的凯塞窗。

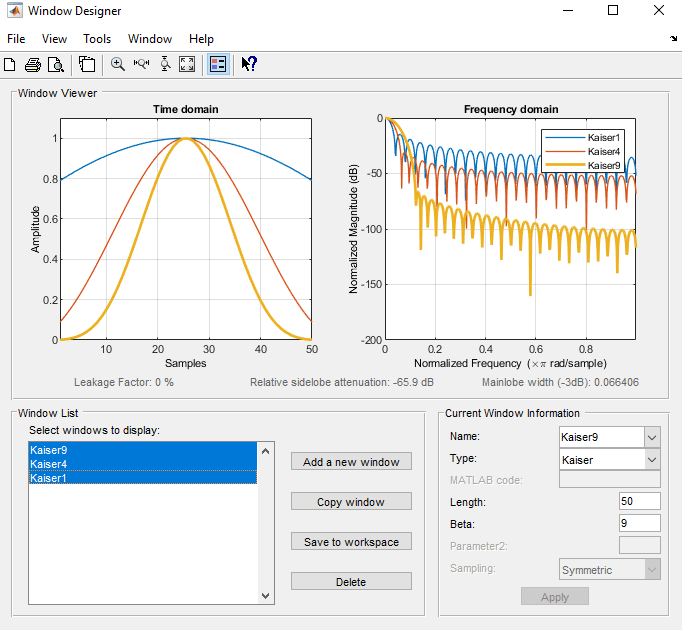
要使用 MATLAB® 命令行创建这些凯塞窗，请键入以下内容：

n = 50;
w1 = kaiser(n,1);
w2 = kaiser(n,4);
w3 = kaiser(n,9);
[W1,f] = freqz(w1/sum(w1),1,512,2);
[W2,f] = freqz(w2/sum(w2),1,512,2);
[W3,f] = freqz(w3/sum(w3),1,512,2);
plot(f,20*log10(abs([W1 W2 W3])))
grid
legend('\beta = 1','\beta = 4','\beta = 9')

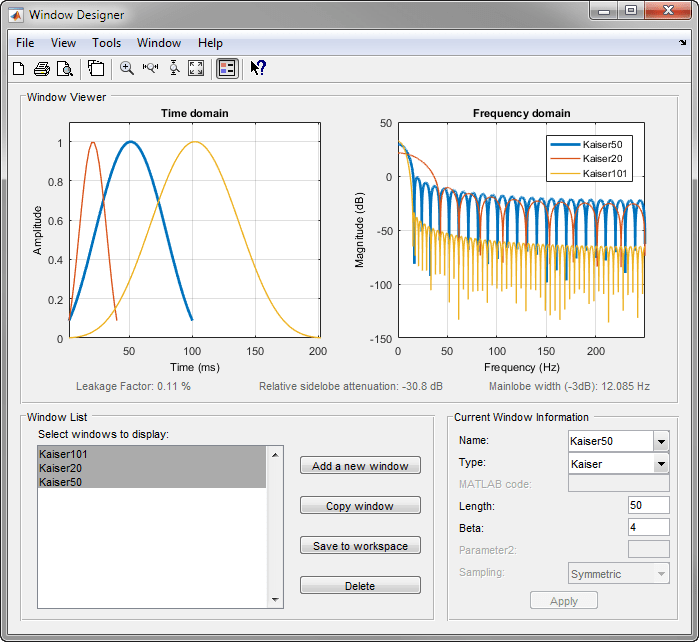
要使用 MATLAB 命令行创建这些凯塞窗，请键入以下内容：

w1 = kaiser(50,4);
w2 = kaiser(20,4);
w3 = kaiser(101,4);
[W1,f] = freqz(w1/sum(w1),1,512,2);
[W2,f] = freqz(w2/sum(w2),1,512,2);
[W3,f] = freqz(w3/sum(w3),1,512,2);
plot(f,20*log10(abs([W1 W2 W3])))
grid
legend('length = 50','length = 20','length = 101')

在 FIR 设计中使用凯塞窗

打开实时脚本

有两个设计公式可以帮助您使用凯塞窗设计 FIR 滤波器，使之满足一组滤波器设定。要获得 –α dB 的相对旁瓣衰减，β (beta) 参数为

β={0.1102(α-8.7),α>50,0.5842(α-21)0.4+0.07886(α-21),50≥α≥21,0,α<21.

要获得 Δω 弧度/采样点的过渡带宽度，请使用长度

n=α-82.285Δω+1.

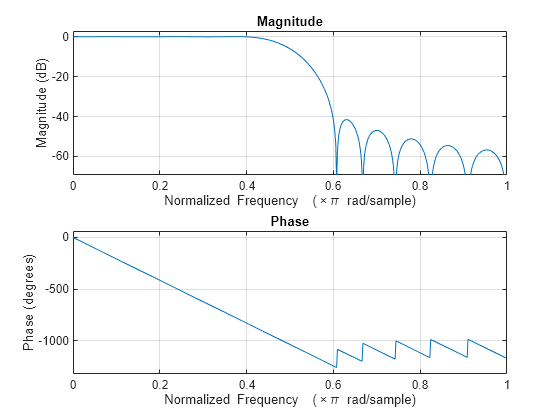
通过上述试探方法设计的滤波器将大致符合设定，但您应该对此进行验证。要设计截止频率为 0.5π 弧度/采样点、过渡带宽度为 0.2π 弧度/采样点、阻带衰减为 40 dB 的低通滤波器，请尝试

[n,wn,beta] = kaiserord([0.4 0.6]*pi,[1 0],[0.01 0.01],2*pi);
h = fir1(n,wn,kaiser(n+1,beta),'noscale');

kaiserord 函数估计滤波器阶数、截止频率和凯塞窗 beta 参数，使之满足一组给定的频域设定。

通带波纹与阻带波纹大致相同。从频率响应可以看出，该滤波器基本上满足设定：

freqz(h,1)

另请参阅

App

函数