峰值分析
此示例说明如何执行基本峰值分析。它将帮助您回答诸如以下的问题:我如何在信号中找到峰值?我如何测量峰值之间的距离?如何测量受趋势影响的信号峰值的振幅?我如何在含噪信号中找到峰值?我如何找到局部最小值?
查找最大值或峰值
苏黎世太阳黑子相对数测量太阳黑子的数量和大小。使用 findpeaks 函数查找峰的位置和值。
load sunspot.dat year = sunspot(:,1); relNums = sunspot(:,2); findpeaks(relNums,year) xlabel("Year") ylabel("Sunspot Number") title("Find All Peaks")

上图以表格形式显示 300 年来太阳黑子的数量,并标出检测到的峰值。下一节说明如何测量这些峰值之间的距离。
测量峰值之间的距离
信号的峰值似乎以固定间隔出现。然而,有些峰彼此非常接近。您可以使用 MinPeakProminence 名称-值参量滤除这些峰值。此示例只考虑两侧相对高差至少为 40 个黑子数的峰。
findpeaks(relNums,year,MinPeakProminence=40) xlabel("Year") ylabel("Sunspot Number") title("Find Prominent Peaks")

以下直方图显示以年数表示的峰值间隔分布:
figure [pks,locs] = findpeaks(relNums,year,MinPeakProminence=40); peakInterval = diff(locs); histogram(peakInterval) grid on xlabel("Year Intervals") ylabel("Frequency of Occurrence") title("Histogram of Peak Intervals (years)")

AverageDistance_Peaks = mean(diff(locs))
AverageDistance_Peaks = 10.9600
该分布显示,大多数峰值间隔在 10 至 12 年之间,表明信号具有周期性。此外,峰值之间的平均间隔为 10.96 年,这与已知的 11 年太阳黑子活动周期相匹配。
寻找裁剪或饱和信号中的峰值
您可能希望将平峰视为峰值或排除它们。如需排除平峰,请使用 Threshold 名称-值参量指定最小偏移,该偏移定义为峰值与其紧邻峰值之间的振幅差。
load clippedpeaks.mat figure % Show all peaks in the first plot tiledlayout("flow") ax(1) = nexttile; findpeaks(saturatedData) xlabel("Samples") ylabel("Amplitude") title("Detecting Saturated Peaks") % Specify a minimum excursion in the second plot ax(2) = nexttile; findpeaks(saturatedData,Threshold=5) xlabel("Samples") ylabel("Amplitude") title("Filtering Out Saturated Peaks") % link and zoom in to show the changes linkaxes(ax(1:2),"xy") axis(ax,[50 70 0 250])

第一个子图显示,对于平峰,上升沿检测为峰值。第二个子图显示,指定阈值有助于排除平峰。
测量峰的振幅
此示例显示 ECG(心电图)信号的峰值分析。ECG 是对随时间变化的心跳活动电信号的测量。该信号由附着在皮肤上的电极测量,对电源干扰和由运动伪影引起的噪声等干扰十分敏感。
load noisyecg.mat t = 1:length(noisyECG_withTrend); figure plot(t,noisyECG_withTrend) title("Signal with Trend") xlabel("Samples"); ylabel("Voltage (mV)") legend("Noisy ECG Signal") grid on

数据去趋势
上述信号显示一个基线偏移,因此不表示真实振幅。为了去趋势,对信号进行某低次多项式拟合,并使用该多项式对信号去趋势。
ECG_data = detrend(noisyECG_withTrend,6); figure plot(t,ECG_data) grid on ax = axis; axis([ax(1:2) -1.2 1.2]) title("Detrended ECG Signal") xlabel("Samples") ylabel("Voltage (mV)") legend("Detrended ECG Signal")

在去趋势后,找到 QRS 复波,它是 ECG 信号中最突出的重复波峰。QRS 复波对应于人心脏左右心室的去极化。它可用于确定患者的心率或预测心脏功能异常。下图显示 ECG 信号中 QRS 复波的形状。
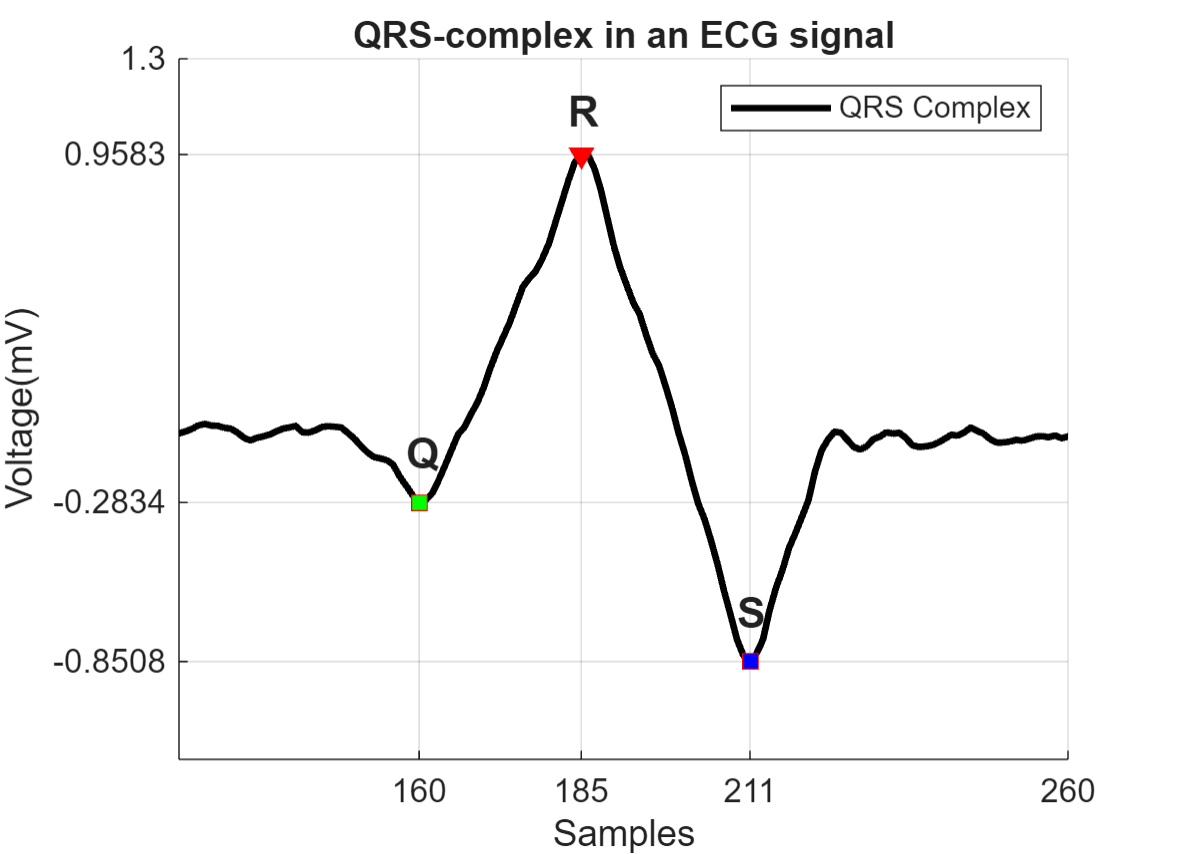
阈值化以找到感兴趣的峰值
QRS 复波由三个主要分量组成:Q 波、R 波、S 波。R 波可以通过设置 0.5 毫伏以上的峰值阈值来检测。注意 R 波相隔 200 多个采样。通过指定 MinPeakDistance 名称-值参量,使用此信息删除不需要的峰值。
[~,locs_Rwave] = findpeaks(ECG_data, ...
MinPeakHeight=0.5,MinPeakDistance=200);为了检测 S 波,找到信号中的局部最小值,并适当应用阈值。
查找信号中的局部最小值
局部最小值可以通过在原始信号的反转版本上找到峰值来检测。
ECG_inverted = -ECG_data;
[~,locs_Swave] = findpeaks(ECG_inverted, ...
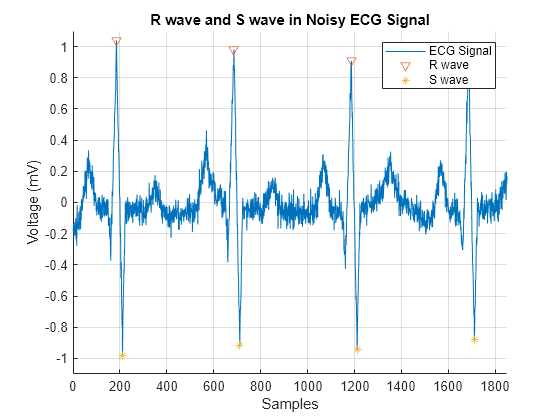
MinPeakHeight=0.5,MinPeakDistance=200);下图显示在信号中检测到的 R 波和 S 波。
figure hold on plot(t,ECG_data) plot(locs_Rwave,ECG_data(locs_Rwave),"v") plot(locs_Swave,ECG_data(locs_Swave),"*") axis([0 1850 -1.1 1.1]) grid on legend("ECG Signal","R wave","S wave") xlabel("Samples") ylabel("Voltage (mV)") title("R wave and S wave in Noisy ECG Signal")
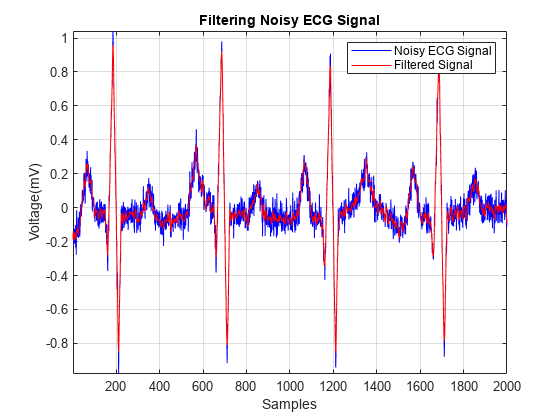
接下来,我们尝试确定 Q 波的位置。对峰值设置阈值以定位 Q 波会导致检测到不需要的峰值,因为 Q 波在噪声中被掩盖。我们先对信号进行滤波,然后找到峰值。萨维茨基-戈雷滤波用于去除信号中的噪声。
smoothECG = sgolayfilt(ECG_data,7,21); figure plot(t,ECG_data,t,smoothECG) grid on axis tight xlabel("Samples") ylabel("Voltage (mV)") legend("Noisy ECG Signal","Filtered Signal") title("Filtering Noisy ECG Signal")
我们对平滑信号执行峰值检测,并使用逻辑索引来找到 Q 波的位置。
[~,min_locs] = findpeaks(-smoothECG,MinPeakDistance=40); % Peaks between -0.2 mV and -0.5 mV locs_Qwave = min_locs(smoothECG(min_locs) > -0.5 ... & smoothECG(min_locs) < -0.2); figure hold on plot(t,smoothECG); plot(locs_Rwave,smoothECG(locs_Rwave),"v") plot(locs_Swave,smoothECG(locs_Swave),"*") plot(locs_Qwave,smoothECG(locs_Qwave),"o") hold off grid on title("Thresholding Peaks in Signal") xlabel("Samples") ylabel("Voltage(mV)") ax = axis; axis([0 1850 -1.1 1.1]) legend("Smooth ECG signal","R wave","S wave","Q wave")

上图显示,在含噪 ECG 信号中成功检测到 QRS 复波。
含噪信号和平滑信号之间的误差
请注意原始信号和去趋势滤波后的信号中的 QRS 复波之间的平均差异。
% Values of the Extrema [val_Qwave, val_Rwave, val_Swave] = deal(smoothECG(locs_Qwave), ... smoothECG(locs_Rwave), smoothECG(locs_Swave)); meanError_Qwave = mean((noisyECG_withTrend(locs_Qwave) - val_Qwave))
meanError_Qwave = 0.2771
meanError_Rwave = mean((noisyECG_withTrend(locs_Rwave) - val_Rwave))
meanError_Rwave = 0.3476
meanError_Swave = mean((noisyECG_withTrend(locs_Swave) - val_Swave))
meanError_Swave = 0.1844
这表明,为了进行高效的峰值分析,必须对含噪信号进行去趋势。
峰值属性
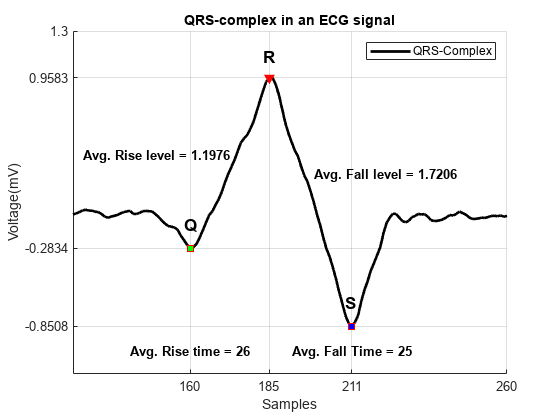
一些重要的峰值属性包括上升时间、下降时间、上升水平和下降水平。为 ECG 信号中的每个 QRS 复波计算这些属性。下图显示这些属性的平均值。
avg_riseTime = mean(locs_Rwave-locs_Qwave); % Average Rise time avg_fallTime = mean(locs_Swave-locs_Rwave); % Average Fall time avg_riseLevel = mean(val_Rwave-val_Qwave); % Average Rise Level avg_fallLevel = mean(val_Rwave-val_Swave); % Average Fall Level helperPeakAnalysisPlot(t,smoothECG, ... locs_Qwave,locs_Rwave,locs_Swave, ... val_Qwave,val_Rwave,val_Swave, ... avg_riseTime,avg_fallTime, ... avg_riseLevel,avg_fallLevel)