findpeaks
查找局部最大值
语法
说明
[___] = findpeaks(___, 支持上述语法中的任何输入参量,且可使用名称-值参量指定选项。Name,Value)
findpeaks(___) 不带输出参量时用于绘制信号并叠加峰值。
示例
定义一个包含三个峰值的向量并绘制该向量。
data = [25 8 15 5 6 10 10 3 1 20 7]; plot(data)
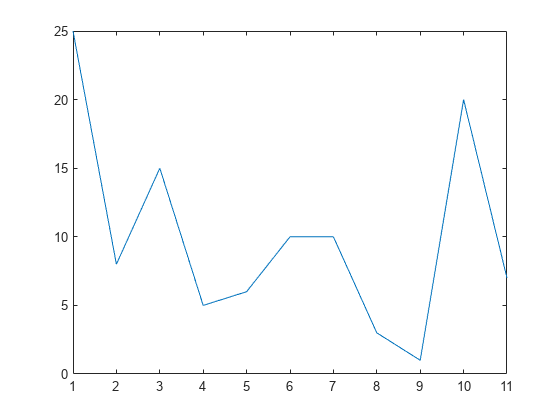
找出局部最大值。峰值按出现的顺序输出。第一个采样不包括在内,尽管它是最大值。对于平峰,该函数仅返回具有最小索引的点。
pks = findpeaks(data)
pks = 1×3
15 10 20
使用不带输出参量的 findpeaks 来显示峰值。
findpeaks(data)

创建一个由几条钟形曲线之和组成的信号。指定每条曲线的位置、高度和宽度。
x = linspace(0,1,1000); Pos = [1 2 3 5 7 8]/10; Hgt = [3 4 4 2 2 3]; Wdt = [2 6 3 3 4 6]/100; for n = 1:length(Pos) Gauss(n,:) = Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2); end PeakSig = sum(Gauss);
绘制各单条曲线及其总和。
plot(x,Gauss,'--',x,PeakSig)
使用具有默认设置的 findpeaks 查找信号的峰值及其位置。
[pks,locs] = findpeaks(PeakSig,x);
使用 findpeaks 绘制峰值并标记它们。
findpeaks(PeakSig,x) text(locs+.02,pks,num2str((1:numel(pks))'))

从最高到最低对峰值进行排序。
[psor,lsor] = findpeaks(PeakSig,x,'SortStr','descend'); findpeaks(PeakSig,x) text(lsor+.02,psor,num2str((1:numel(psor))'))
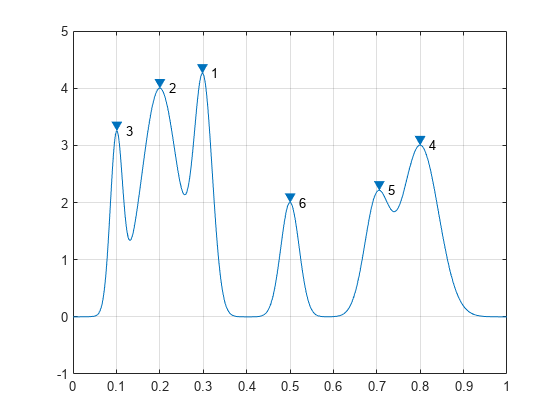
创建一个由分布在一个完整余弦周期上的几条钟形曲线之和组成的信号。指定每条曲线的位置、高度和宽度。
x = linspace(0,1,1000); base = 4*cos(2*pi*x); Pos = [1 2 3 5 7 8]/10; Hgt = [3 7 5 5 4 5]; Wdt = [1 3 3 4 2 3]/100; for n = 1:length(Pos) Gauss(n,:) = Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2); end PeakSig = sum(Gauss)+base;
绘制各单条曲线及其总和。
plot(x,Gauss,'--',x,PeakSig,x,base)
使用 findpeaks 定位并绘制相对高差至少为 4 的峰值。
findpeaks(PeakSig,x,'MinPeakProminence',4,'Annotate','extents')
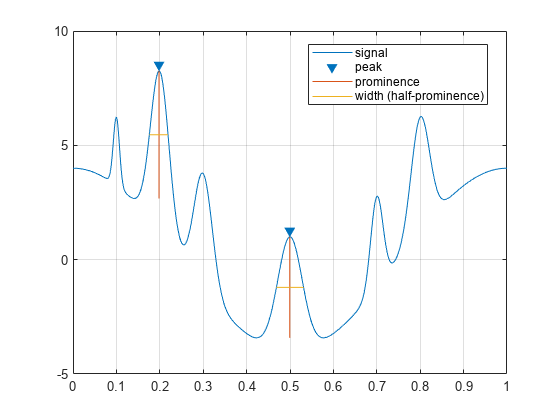
只有最高和最低峰值满足该条件。
显示所有峰值的相对高差以及相对高差一半处的峰宽。
[pks,locs,widths,proms] = findpeaks(PeakSig,x); widths
widths = 1×6
0.0154 0.0431 0.0377 0.0625 0.0274 0.0409
proms
proms = 1×6
2.6816 5.5773 3.1448 4.4171 2.9191 3.6363
太阳黑子是一种周期性出现的现象。已知其数量大约每 11 年达到峰值。
加载文件 sunspot.dat,其中包含从 1700 年到 1987 年每年观测到的太阳黑子的平均数量。查找并绘制最大值。
load sunspot.dat
year = sunspot(:,1);
avSpots = sunspot(:,2);
findpeaks(avSpots,year)
通过忽略间距非常近的峰值来改进对周期持续时间的估计。再次查找并绘制峰值,但现在将可接受的峰间距限制为大于 6 年。
findpeaks(avSpots,year,'MinPeakDistance',6)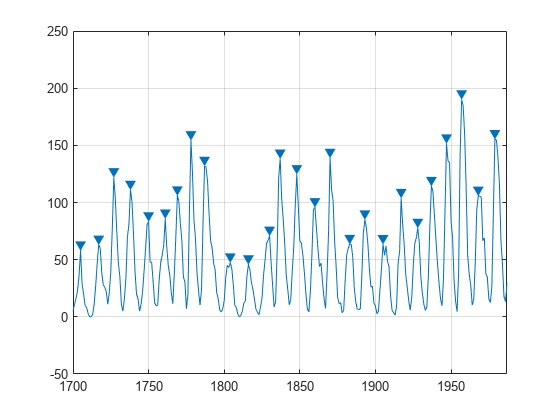
使用 findpeaks 返回的峰值位置来计算最大值之间的均值间距。
[pks,locs] = findpeaks(avSpots,year,'MinPeakDistance',6);
meanCycle = mean(diff(locs))meanCycle = 10.9600
使用年份数据创建一个 datetime 数组。假设太阳黑子是在每年 3 月 20 日(接近春分)统计的。找出太阳黑子的峰值年份。使用 years 函数将最小峰间距指定为 duration。
ty = datetime(year,3,20); [pk,lk] = findpeaks(avSpots,ty,'MinPeakDistance',years(6)); plot(ty,avSpots,lk,pk,'o')
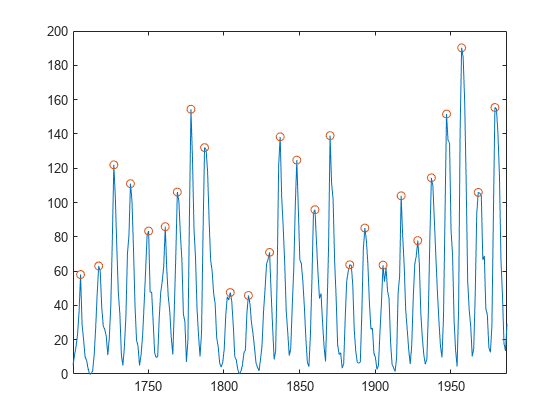
使用 datetime 功能计算太阳黑子的均值周期。
dttmCycle = years(mean(diff(lk)))
dttmCycle = 10.9600
用这些数据创建一个时间表。以年为单位指定时间变量。绘制数据图。显示该时间表的最后五个条目。
TT = timetable(years(year),avSpots); plot(TT.Time,TT.Variables)
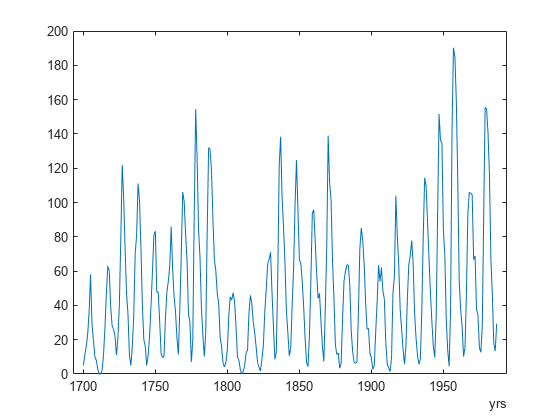
entries = TT(end-4:end,:)
entries=5×1 timetable
Time avSpots
________ _______
1983 yrs 66.6
1984 yrs 45.9
1985 yrs 17.9
1986 yrs 13.4
1987 yrs 29.3
加载一段以 7418 Hz 采样的音频信号。选择 200 个采样。
load mtlb
select = mtlb(1001:1200);找出间隔至少为 5 ms 的峰值。
为了应用此约束,findpeaks 选择信号中最高的峰值,并消除在其 5 ms 范围内的所有峰值。然后,该函数对剩余峰值中的最高峰值重复该过程并进行迭代,直到处理完要考虑的所有峰值。
findpeaks(select,Fs,'MinPeakDistance',0.005)
找出振幅至少为 1 V 的峰值。
findpeaks(select,Fs,'MinPeakHeight',1)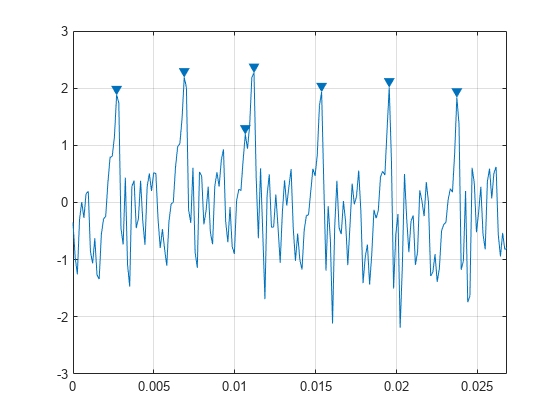
找出比相邻采样至少高 1 V 的峰值。
findpeaks(select,Fs,'Threshold',1)
找出信号在抵达更高峰值前于任一侧下降至少 1 V 的峰值。
findpeaks(select,Fs,'MinPeakProminence',1)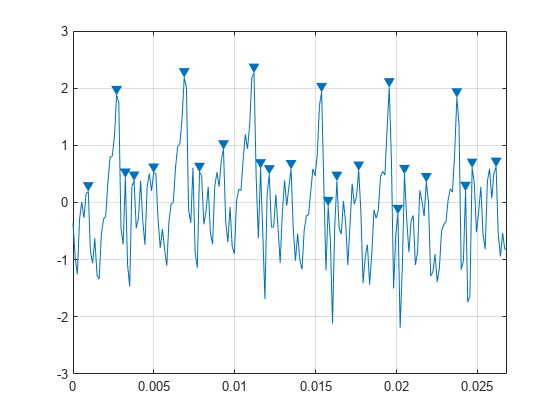
如果数据大于给定的饱和点,传感器可以返回裁剪后的读数。您可以选择忽略这些没有意义的峰值,也可以选择将它们纳入您的分析中。
生成一个由频率为 5 Hz 和 3 Hz 的三角函数的乘积组成的信号,嵌入方差为 0.1² 的高斯白噪声中。信号以 100 Hz 的速率进行采样,持续时间为一秒。重置随机数生成器以获得可重现的结果。
rng default
fs = 1e2;
t = 0:1/fs:1-1/fs;
s = sin(2*pi*5*t).*sin(2*pi*3*t)+randn(size(t))/10;通过截断大于 0.32 的指定边界的每个读数来模拟经过饱和处理的测量值。绘制经过饱和处理的信号。
bnd = 0.32;
s(s>bnd) = bnd;
plot(t,s)
xlabel('Time (s)')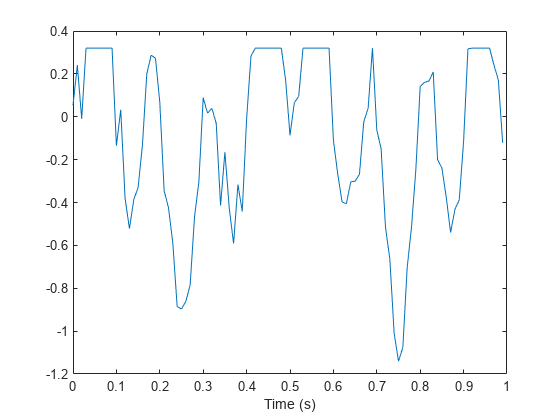
找到信号的峰值。findpeaks 仅报告每个平峰的上升沿。
[pk,lc] = findpeaks(s,t); hold on plot(lc,pk,'x')
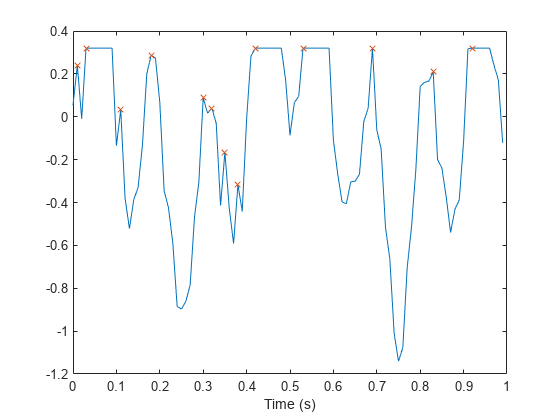
使用 'Threshold' 名称-值对组排除平峰。要求峰值与其相邻峰值之间的最小振幅差为 。
[pkt,lct] = findpeaks(s,t,'Threshold',1e-4); plot(lct,pkt,'o','MarkerSize',12)
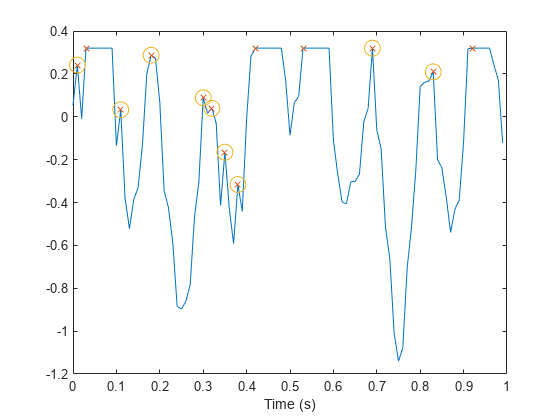
创建一个由几条钟形曲线之和组成的信号。指定每条曲线的位置、高度和宽度。
x = linspace(0,1,1000); Pos = [1 2 3 5 7 8]/10; Hgt = [4 4 2 2 2 3]; Wdt = [3 8 4 3 4 6]/100; for n = 1:length(Pos) Gauss(n,:) = Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2); end PeakSig = sum(Gauss);
绘制各单条曲线及其总和。
plot(x,Gauss,'--',x,PeakSig)
grid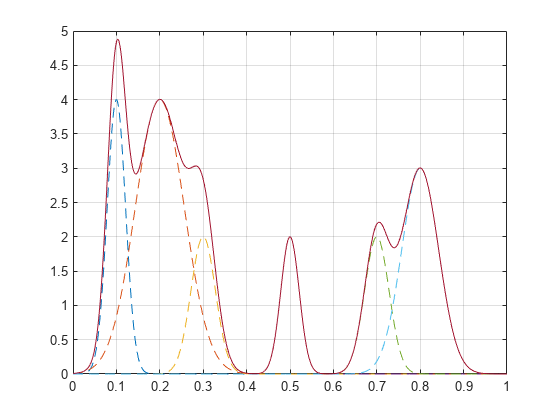
在相对高差的一半处测量波峰的宽度。
findpeaks(PeakSig,x,'Annotate','extents')

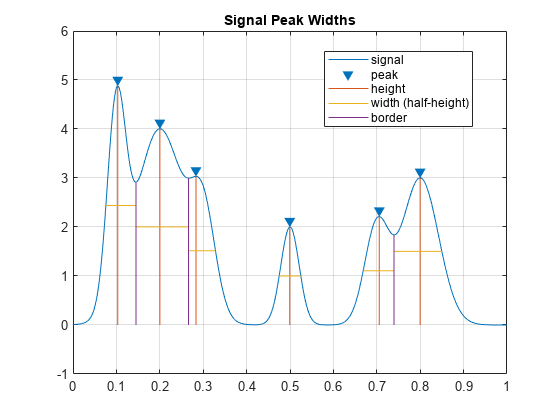
再次测量宽度,这次在半高处测量。
findpeaks(PeakSig,x,'Annotate','extents','WidthReference','halfheight') title('Signal Peak Widths')
使用具有 sinc 函数核的非线性最小二乘法获得一个信号中两个主要峰值的细化峰值位置估计。
生成信号
线性 FM 波形的雷达脉冲压缩产生一个正弦形状的频谱,其中峰值频率位置与雷达和探测对象之间的距离成正比。您可以先使用findpeaks估计峰值位置和振幅,然后使用refinepeaks增强您的估计。此示例查找合成无噪声脉冲压缩信号的峰值振幅和位置,并使用 refinepeaks 改进估计。
生成一个由两个正弦波形组成的信号,峰值分别为在 4.76 kHz 和 35.8 kHz 处的 1 和 1.5。将频率间距设为 2.5 Hz。
aTarget = [1 1.5]; fTarget = 1e3*[4.76 35.8]; freqkHzFull = (0:0.0025:50)'; waveFull = abs(sinc([1 0.5].*(freqkHzFull-fTarget/1e3)))*aTarget';
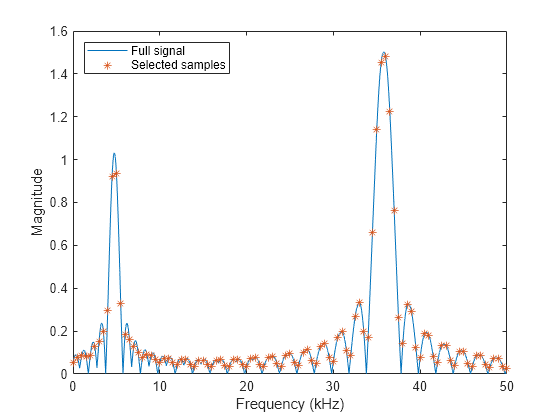
以 200 为因子对信号下采样,因此采样之间的频率间距为 0.5 kHz。此示例细化下采样信号峰值的振幅和位置估计,并将改进的估计与原始信号中的值进行比较。
freq = downsample(freqkHzFull,200); wave = downsample(waveFull,200); plot(freqkHzFull,waveFull,freq,wave,"*") legend(["Full signal" "Selected samples"],Location="northwest") xlabel("Frequency (kHz)") ylabel("Magnitude")
使用非线性最小二乘细化峰值
使用 findpeaks 对信号的两个最高峰值的振幅、位置和半高宽度进行初始估计。
[PV,PL,PW] = findpeaks(wave,NPeaks=2, ... SortStr="descend",WidthReference="halfheight");
使用 refinepeaks 增强使用非线性最小二乘 (NLS) 方法的峰值估计。指定信号的频率点和峰值宽度。峰值明显更接近预期值 1.5 和 1,而频率位置分别很好地逼近 35.8 kHz 和 4.76 kHz。
LW = max(PW,2);
[Ypk,Xpk] = refinepeaks(wave,PL,freq,Method="NLS",LobeWidth=LW)Ypk = 2×1
1.5063
1.0163
Xpk = 2×1
35.8001
4.7628
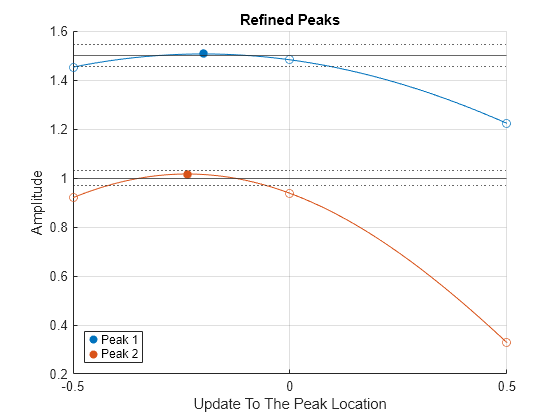
在 y 轴上绘制细化峰值的振幅,在 x 轴上绘制与初始峰值估计相比的更新后的峰值位置。两个初始估计的峰值和它们周围的两个采样都相隔 0.5 kHz。由实心圆指示的细化峰值显示实际峰值位置与初始估计的峰值位置的对比以及校正后的振幅。
refinepeaks(wave,PL,freq,Method="NLS",LobeWidth=LW) yline(aTarget) % Theoretical peak amplitudes errorBounds = aTarget.*(1+0.03*[-1;1]); yline(errorBounds(:),":") % ±3% error bounds legend("Peak "+[1 2])
输入参数
名称-值参数
将可选参量对组指定为 Name1=Value1,...,NameN=ValueN,其中 Name 是参量名称,Value 是对应的值。名称-值参量必须出现在其他参量之后,但对各个参量对组的顺序没有要求。
如果使用的是 R2021a 之前的版本,请使用逗号分隔每个名称和值,并用引号将 Name 引起来。
示例: findpeaks(y,x,SortStr="descend",NPeaks=3) 查找信号 y 的三个最高峰值。
要返回的最大峰值数,指定为正整数标量。findpeaks 从输入数据的第一个元素开始运算,并在峰值数量达到值 'NPeaks' 时终止。
数据类型: double | single
峰值排序,指定为以下值之一:
'none'按照峰值在输入数据中出现的顺序返回峰值。'ascend'按升序或递增顺序(从最小值到最大值)返回峰值。'descend'按降序(从最大值到最小值)返回峰值。
最小峰值高度,指定为实数标量。使用此参量可使 findpeaks 仅返回高于 'MinPeakHeight' 的峰值。指定最小峰值高度可以减少处理时间。
数据类型: double | single
最小峰值相对高差,指定为非负实数标量。使用此参量可使 findpeaks 仅返回那些相对高差至少为 'MinPeakProminence' 的峰值。有关详细信息,请参阅相对高差。
数据类型: double | single
峰值与其邻点之间的最小高度差,指定为非负实数标量。使用此参量可使 findpeaks 仅返回与紧邻峰值的高度差至少为 'Threshold' 值的那些峰值。
数据类型: double | single
最小峰间距,指定为正实数标量。当您为 'MinPeakDistance' 指定值时,算法会选择信号中最高的峰值,并忽略在其 'MinPeakDistance' 范围内的所有峰值。然后,该函数对剩余峰值中的最高峰值重复该过程并进行迭代,直到处理完要考虑的所有峰值。
使用此参量可以让 findpeaks 忽略在较大峰值的邻域中出现的小峰值。
数据类型: double | single | duration
宽度测量值的参考高度,指定为 'halfprom' 或 'halfheight'。findpeaks 将峰宽估计为下降信号与水平参考线相交点(截距点)之间的距离。使用在 'WidthReference' 中指定的标准选择参考线的高度:
'halfprom'将参考线定位在峰值下方,垂直距离等于峰值相对高差的一半。有关详细信息,请参阅相对高差。'halfheight'将参考线定位在峰值高度的一半处。如果参考线的任何截距点落在了'MinPeakHeight'、'MinPeakProminence'和'Threshold'设置所确定的峰值的边界之外,则该参考线将被截断。峰值之间的边界由峰值之间最低波谷的水平位置确定。高度小于零的峰值将被丢弃。
截距点的位置通过线性插值计算得出。
绘图样式,指定为以下值之一:
'peaks'绘制信号并对每个峰值的位置和数值进行注解。'extents'绘制信号并对每个峰值的位置、数值、宽度和相对高差进行注解。
如果带输出参量调用 findpeaks,则此参量将被忽略。
输出参量
局部最大值,以信号值的向量形式返回。如果没有局部最大值,则 pks 为空。
峰宽,以实数向量形式返回。每个峰值的宽度计算为峰值左右两侧与参考线相交的两点之间的距离,参考线的高度由 WidthReference 指定。交点本身通过线性插值求得。
峰值相对高差,以实数向量形式返回。峰值的相对高差是信号在峰值两侧必须至少下降多少垂直距离,才会再次上升到比该峰值更高的峰值或达到两侧端点(无更高峰值时)。有关详细信息,请参阅相对高差。
详细信息
峰值的相对高差根据峰值本身高度及其相对于其他峰值的位置衡量其突出程度。较矮的孤立峰值可能会比虽然较高但在高峰范围中并不显著的一员更加突出。
要测量峰值的相对高差,请执行以下步骤:
在峰值上放一个标记。
从峰值向左右延伸一条水平线,直到该线出现以下情况之一:
穿过信号,因为出现更高的峰值
到达信号的左端或右端
找出步骤 2 中定义的两个区间中每个区间内的信号最小值。此点是波谷或信号端点之一。
在两个区间的最小值中,较高者即为参考水平。在此水平以上的峰值高度就是其相对高差。
findpeaks 对端点之外的信号行为不做假设,无论其高度如何。因此,步骤 2 和 4 会忽略端点以外的信号行为,该行为通常会影响参考水平的值。例如,假设此信号的峰值如下:
| 峰值编号 | 左区间位于峰值和以下值之间 | 右区间位于峰值和以下值之间 | 左区间内的最低点 | 右区间内的最低点 | 参考水平(最高最小值) |
|---|---|---|---|---|---|
| 1 | 左端 | 因峰值 2 产生的交叉点 | 左端点 | a | a |
| 2 | 左端 | 右端 | 左端点 | h | 左端点 |
| 3 | 因峰值 2 产生的交叉点 | 因峰值 4 产生的交叉点 | b | c | c |
| 4 | 因峰值 2 产生的交叉点 | 因峰值 6 产生的交叉点 | b | d | b |
| 5 | 因峰值 4 产生的交叉点 | 因峰值 6 产生的交叉点 | d | e | e |
| 6 | 因峰值 2 产生的交叉点 | 右端 | d | h | d |
| 7 | 因峰值 6 产生的交叉点 | 因峰值 8 产生的交叉点 | f | g | g |
| 8 | 因峰值 6 产生的交叉点 | 右端 | f | h | f |
| 9 | 因峰值 8 产生的交叉点 | 穿过信号(由于存在右端点) | h | i | i |
提示
您可以使用 findpeaks 初始估计信号峰值,然后使用 refinepeaks 增强其振幅和位置。
假设您有振幅为 y 且位置为 x 的信号。以下代码片段显示如何根据 y 和 x 估计和细化峰值。
[yPeaks,xPeaksIdx] = findpeaks(y); [yRPeaks,xRPeaks] = refinepeaks(y,xPeaksIdx,x)
扩展功能
用法说明和限制:
findpeaks函数不支持用于代码生成的datetime输入。
用法说明和限制:
findpeaks函数不支持用于代码生成的datetime输入。
此函数完全支持 GPU 数组。有关详细信息,请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。
版本历史记录
在 R2007b 中推出findpeaks 函数支持图形处理单元 (GPU) 的代码生成。您必须拥有 MATLAB® Coder™ 和 GPU Coder™ 才能生成 CUDA® 代码。
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)