信号生成和可视化
此示例说明如何使用 Signal Processing Toolbox™ 中提供的函数生成广泛使用的周期和非周期性波形、扫频正弦波和脉冲序列。
周期性波形
除了 MATLAB® 中的 sin 和 cos 函数外,Signal Processing Toolbox™ 还提供其他函数(如 sawtooth 和 square)来生成周期性信号。
sawtooth 函数生成锯齿波,波峰在 ,周期为 。可选宽度参数以 的小数倍来指定信号最大值出现的位置。
square 函数生成周期为 的方波。可选参数指定占空比,即信号为正的周期的百分比。
以 10 kHz 的采样率生成 1.5 秒的 50 Hz 锯齿波。对一个方波进行重复计算。
fs = 10000; t = 0:1/fs:1.5; x1 = sawtooth(2*pi*50*t); x2 = square(2*pi*50*t); nexttile plot(t,x1) axis([0 0.2 -1.2 1.2]) xlabel("Time (sec)") ylabel("Amplitude") title("Sawtooth Periodic Wave") nexttile plot(t,x2) axis([0 0.2 -1.2 1.2]) xlabel("Time (sec)") ylabel("Amplitude") title("Square Periodic Wave")

非周期性波形
为了生成三角形、矩形和高斯脉冲,工具箱提供了 tripuls、rectpuls 和 gauspuls 函数。
tripuls 函数生成以 t = 0 为中心、默认宽度为 1 的采样非周期性单位高度三角形脉冲。
rectpuls 函数生成以 t = 0 为中心、默认宽度为 1 的采样非周期性单位高度矩形脉冲。非零振幅的区间定义为在右侧开放:rectpuls(-0.5) = 1,而 rectpuls(0.5) = 0。
生成 2 秒的三角形脉冲,采样率为 10 kHz,宽度为 20 ms。对一个矩形脉冲进行重复计算。
fs = 10000; t = -1:1/fs:1; x1 = tripuls(t,20e-3); x2 = rectpuls(t,20e-3); figure nexttile plot(t,x1) axis([-0.1 0.1 -0.2 1.2]) xlabel("Time (sec)") ylabel("Amplitude") title("Triangular Aperiodic Pulse") nexttile plot(t,x2) axis([-0.1 0.1 -0.2 1.2]) xlabel("Time (sec)") ylabel("Amplitude") title("Rectangular Aperiodic Pulse")

gauspuls 函数使用指定时间、中心频率和小数带宽生成高斯调制正弦脉冲。
sinc 函数计算输入向量或矩阵的数学正弦函数。正弦函数是宽度为 ,高度为单位高度的矩形脉冲的连续傅里叶逆变换。
生成带宽为 60%、采样率为 1 MHz 的 50 kHz 高斯 RF 脉冲。当包络比峰值低 40 dB 时,截断脉冲。
tc = gauspuls("cutoff",50e3,0.6,[],-40);
t1 = -tc : 1e-6 : tc;
y1 = gauspuls(t1,50e3,0.6);为一个线性间距向量生成正弦函数:
t2 = linspace(-5,5); y2 = sinc(t2); figure nexttile plot(t1*1e3,y1) xlabel("Time (ms)") ylabel("Amplitude") title("Gaussian Pulse") nexttile plot(t2,y2) xlabel("Time (sec)") ylabel("Amplitude") title("Sinc Function")

扫频波形
工具箱还提供生成扫频波形的函数,如 chirp 函数。两个可选参数以度为单位指定替代扫描方法和初始相位。下面是使用 chirp 函数生成线性或二次、凸和凹二次啁啾信号的几个示例。
生成以 1 kHz 进行 2 秒采样的线性啁啾信号。瞬时频率在 t = 0 处为 100 Hz,在 t = 1 秒处超出 250 Hz。
tlin = 0:0.001:2; ylin = chirp(tlin,100,1,250);
生成以 1 kHz 进行 4 秒采样的二次啁啾信号。瞬时频率在 t = 0 处为 100 Hz,在 t = 1 秒处超出 200 Hz。
tq = -2:0.001:2;
yq = chirp(tq,100,1,200,"quadratic");计算并显示啁啾信号的频谱图。
figure nexttile pspectrum(ylin,tlin,"spectrogram", ... Leakage=0.85,TimeResolution=0.1,OverlapPercent=99) title("Linear Chirp") nexttile pspectrum(yq,tq,"spectrogram", ... Leakage=0.85,TimeResolution=0.1,OverlapPercent=99) title("Quadratic Chirp")

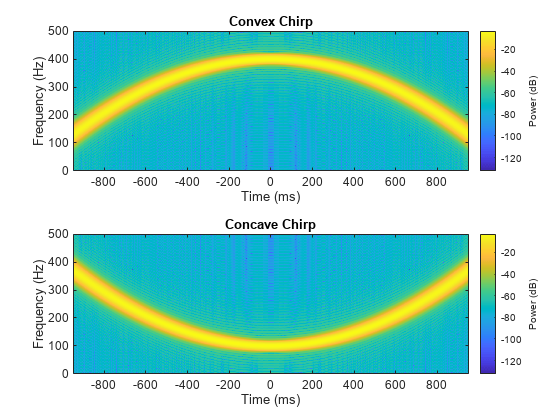
生成以 1 kHz 采样 2 秒的凸二次啁啾信号。瞬时频率在 t = 0 处为 100 Hz,在 t = 1 处时增大到 400 Hz。
tcx = -1:0.001:1; fo = 100; f1 = 400; ycx = chirp(tcx,fo,1,f1,"quadratic",[],"convex");
生成以 1 kHz 进行 2 秒采样的凹二次啁啾信号。瞬时频率在 t = 0 处为 400 Hz,在 t = 1 秒处降低至 100 Hz。
tcv = -1:0.001:1; fo = 400; f1 = 100; ycv = chirp(tcv,fo,1,f1,"quadratic",[],"concave");
计算并显示啁啾信号的频谱图。
figure nexttile pspectrum(ycx,tcx,"spectrogram", ... Leakage=0.85,TimeResolution=0.1,OverlapPercent=99) title("Convex Chirp") nexttile pspectrum(ycv,tcv,"spectrogram", ... Leakage=0.85,TimeResolution=0.1,OverlapPercent=99) title("Concave Chirp")
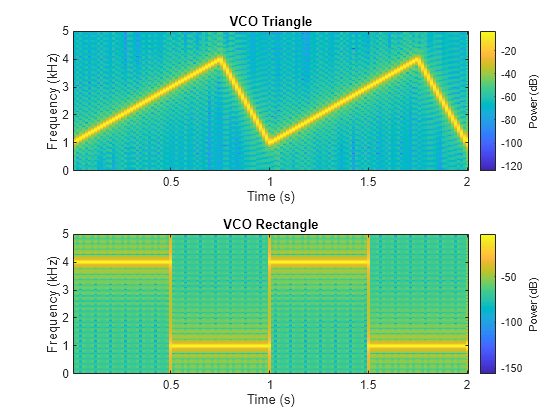
另一个函数生成器是 vco(压控振荡器),它生成以输入向量确定的频率振荡的信号。输入向量可以是三角形、矩形或正弦波等。
生成以 10 kHz 采样的 2 秒信号,其瞬时频率为三角形。对一个矩形进行重复计算。
fs = 10000; t = 0:1/fs:2; x1 = vco(sawtooth(2*pi*t,0.75),[0.1 0.4]*fs,fs); x2 = vco(square(2*pi*t),[0.1 0.4]*fs,fs);
绘制生成的信号的频谱图。
figure nexttile pspectrum(x1,t,"spectrogram", ... Leakage=0.9,FrequencyResolution=55) title("VCO Triangle") nexttile pspectrum(x2,t,"spectrogram", ... Leakage=0.9,FrequencyResolution=55) title("VCO Rectangle")
脉冲序列
要生成脉冲序列,您可以使用 pulstran 函数。
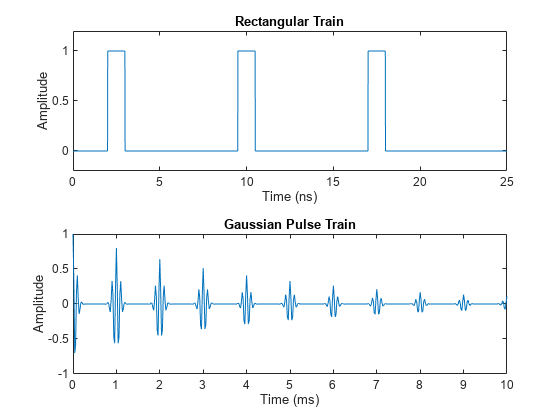
构造一个 1 纳秒矩形脉冲序列,它以 7.5 纳秒的间距和 100 GHz 的速率采样。
fs = 100e9; D = [2.5 10 17.5]' * 1e-9; t = 0 : 1/fs : 2500/fs; w = 1e-9; yp = pulstran(t,D,@rectpuls,w);
生成 10 kHz、50% 带宽的周期性高斯脉冲信号。脉冲重复频率为 1 kHz,采样率为 50 kHz,脉冲序列长度为 10 毫秒。重复振幅每次应按 0.8 衰减。使用函数句柄指定生成器函数。
T = 0 : 1/50e3 : 10e-3; D = [0 : 1/1e3 : 10e-3 ; 0.8.^(0:10)]'; Y = pulstran(T,D,@gauspuls,10e3,.5); figure nexttile plot(t*1e9,yp) axis([0 25 -0.2 1.2]) xlabel("Time (ns)") ylabel("Amplitude") title("Rectangular Train") nexttile plot(T*1e3,Y) xlabel("Time (ms)") ylabel("Amplitude") title("Gaussian Pulse Train")
另请参阅
chirp | gauspuls | pulstran | rectpuls | sawtooth | sin | sinc | square | tripuls | vco