Significance Testing for Periodic Component

This example shows how to assess the significance of a sinusoidal component in white noise using Fisher's g-statistic. Fisher's g-statistic is the ratio of the largest periodogram value to the sum of all the periodogram values over 1/2 of the frequency interval, (0, Fs/2). A detailed description of the g-statistic and exact distribution can be found in the references.

Create a signal consisting of a 100 Hz sine wave in white Gaussian noise with zero mean and variance 1. The amplitude of the sine wave is 0.25. The sample rate is 1 kHz. Set the random number generator to the default settings for reproducible results.

rng("default")

Fs = 1e3;
t = 0:1/Fs:1-1/Fs;
x = 0.25*cos(2*pi*100*t) + randn(size(t));

Obtain the periodogram of the signal using periodogram. Exclude 0 and the Nyquist frequency (Fs/2). Plot the periodogram.

[Pxx,F] = periodogram(x,rectwin(length(x)),length(x),Fs);
Pxx = Pxx(2:length(x)/2);

periodogram(x,rectwin(length(x)),length(x),Fs)

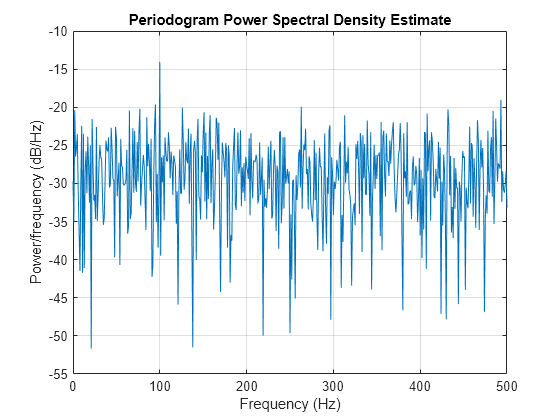
Find the maximum value of the periodogram. Fisher's g-statistic is the ratio of the maximum periodogram value to the sum of all periodogram values.

[maxval,index] = max(Pxx);
fisher_g = Pxx(index)/sum(Pxx)

fisher_g = 
0.0381

The maximum periodogram value occurs at 100 Hz, which you can verify by finding the frequency corresponding to the index of the maximum periodogram value.

F = F(2:end-1);
F(index)

ans = 
100

Use the distributional results detailed in the references to determine the significance level, pval, of Fisher's g-statistic. The following MATLAB® code implements equation (6) of [2]. Use the logarithm of the gamma function to avoid overflows when computing binomial coefficients.

N = length(Pxx);
nn = 1:floor(1/fisher_g);

I = (-1).^(nn-1).*exp(gammaln(N+1)-gammaln(nn+1)-gammaln(N-nn+1)) ...
    .*(1-nn*fisher_g).^(N-1);

pval = sum(I)

pval = 
2.0163e-06

The p-value is less than 0.00001, which indicates a significant periodic component at 100 Hz. The interpretation of Fisher's g-statistic is complicated by the presence of other periodicities. See [1] for a modification when multiple periodicities may be present.

References

[1] Percival, Donald B. and Andrew T. Walden. Spectral Analysis for Physical Applications. Cambridge, UK: Cambridge University Press, 1993.

[2] Wichert, Sofia, Konstantinos Fokianos, and Korbinian Strimmer. "Identifying Periodically Expressed Transcripts in Microarray Time Series Data." Bioinformatics. Vol. 20, 2004, pp. 5-20.

See Also

nchoosek | periodogram