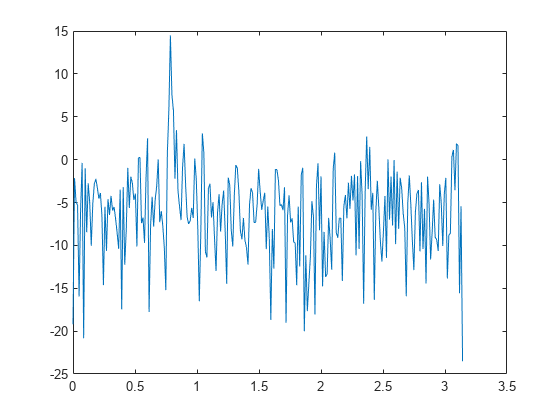
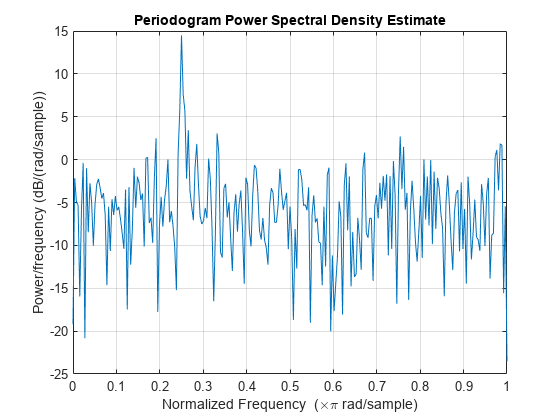
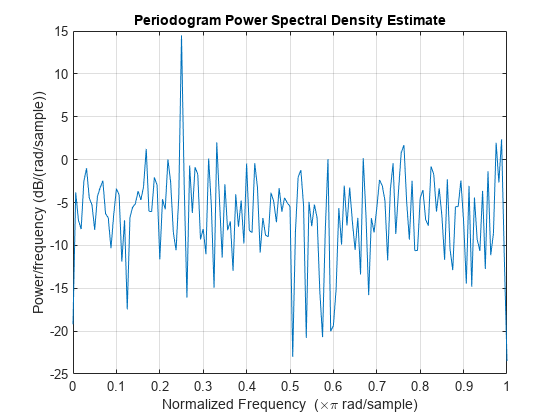
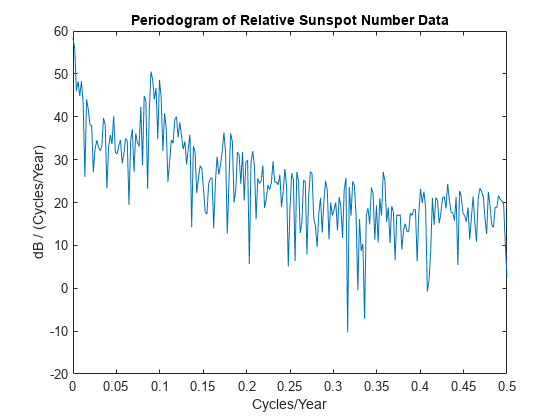
periodogram
周期图功率谱密度估计值
语法
说明
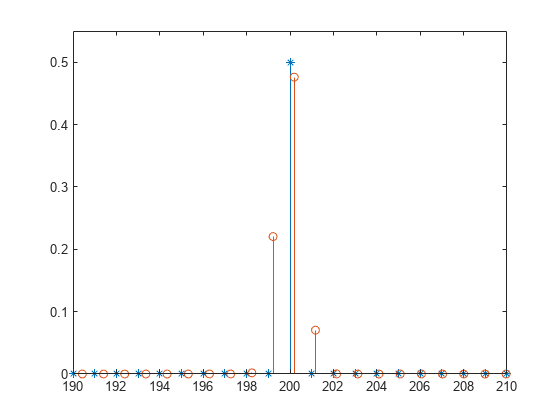
[___, 在 pxxc] = periodogram(___,'ConfidenceLevel',probability)pxxc 中返回 PSD 估计值的 probability × 100% 置信区间。
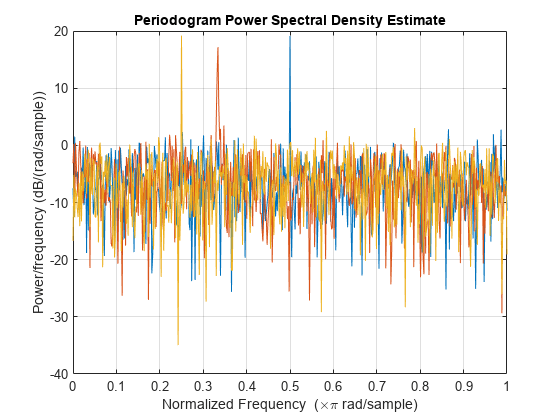
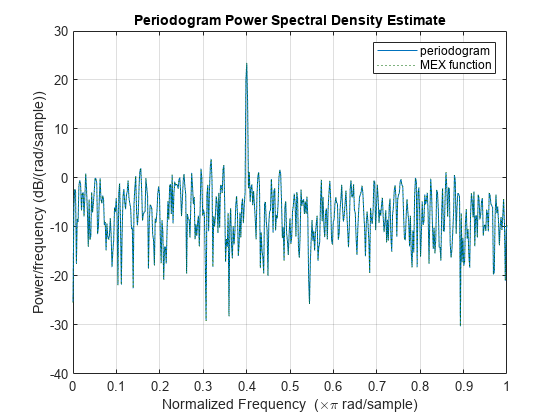
[___] = periodogram(___, 在 spectrumtype)spectrumtype 指定为 'psd' 时返回 PSD 估计值，在 spectrumtype 指定为 'power' 时返回功率谱。
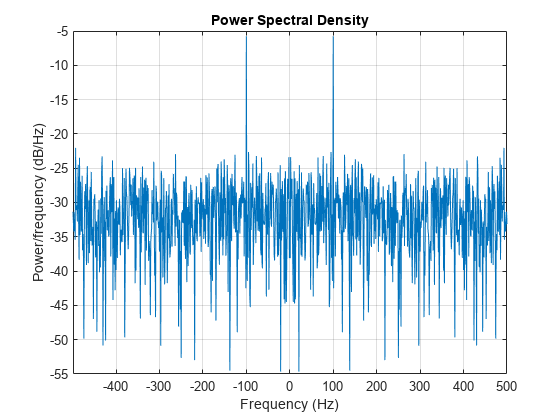
不带输出参量的 periodogram(___) 在当前图窗窗口中绘制周期图 PSD 估计值或功率谱。
示例
获取一个输入信号的周期图，该输入信号由角频率为 弧度/采样点的离散时间正弦信号和加性 白噪声组成。
创建一个角频率为 弧度/采样点并具有加性 白噪声的正弦波。信号长度为 320 个采样。使用默认矩形窗和 DFT 长度获取周期图。DFT 长度是大于信号长度的下一个 2 的幂，或 512 个点。由于信号是实数值且具有偶数长度，周期图是单边周期图，并且有 512/2+1 个点。
n = 0:319; x = cos(pi/4*n)+randn(size(n)); [pxx,w] = periodogram(x); plot(w,10*log10(pxx))
使用 periodogram 且以无输出形式重复绘图。
periodogram(x)
获取一个输入信号的修正周期图，该输入信号由角频率为 弧度/采样点的离散时间正弦信号和加性 白噪声组成。
创建一个角频率为 弧度/采样并具有加性 白噪声的正弦波。信号长度为 320 个采样。使用汉明窗和默认 DFT 长度获取修正周期图。DFT 长度是大于信号长度的下一个 2 的幂，或 512 个点。由于信号是实数值且具有偶数长度，周期图是单边周期图，并且有 512/2+1 个点。
n = 0:319; x = cos(pi/4*n)+randn(size(n)); periodogram(x,hamming(length(x)))
获取一个输入信号的周期图，该输入信号由角频率为 弧度/采样点的离散时间正弦信号和加性 白噪声组成。使用等于信号长度的 DFT 长度。
创建一个角频率为 弧度/采样并具有加性 白噪声的正弦波。信号长度为 320 个采样。使用默认矩形窗和等于信号长度的 DFT 长度获取周期图。由于信号是实数值信号，默认返回单边周期图，长度等于 320/2+1。
n = 0:319; x = cos(pi/4*n)+randn(size(n)); nfft = length(x); periodogram(x,[],nfft)
获取在 1700 年至 1987 年间每年采样的 Wolf（相对太阳黑子）数量数据的周期图。
加载相对太阳黑子数量数据。使用默认矩形窗和 DFT 点数（此示例中为 512）获取周期图。这些数据的采样率为 1 采样/年。绘制周期图。
load sunspot.dat relNums=sunspot(:,2); [pxx,f] = periodogram(relNums,[],[],1); plot(f,10*log10(pxx)) xlabel('Cycles/Year') ylabel('dB / (Cycles/Year)') title('Periodogram of Relative Sunspot Number Data')
您在前面的图窗中看到，在周期图中大约 0.1 周期/年处有一个峰值，这表明周期大约为 10 年。
获取一个输入信号的周期图，该输入信号由处于加性 白噪声中的角频率为 和 弧度/采样点的两个离散时间正弦信号组成。获取在 和 弧度/采样点处的双边周期图估计值。将结果与单边周期图进行比较。
n = 0:319; x = cos(pi/4*n)+0.5*sin(pi/2*n)+randn(size(n)); [pxx,w] = periodogram(x,[],[pi/4 pi/2]); pxx
pxx = 1×2
14.0589 2.8872
[pxx1,w1] = periodogram(x); plot(w1/pi,pxx1,w/pi,2*pxx,'o') legend('pxx1','2 * pxx') xlabel('\omega / \pi')
获得的周期图值是单边周期图中值的 1/2。当您在一组特定频率处计算周期图时，输出是双边估计值。
创建一个信号，该信号由处于 N(0,1) 加性白噪声中频率为 100 和 200 Hz 的两个正弦波组成。采样频率为 1 kHz。获取在 100 和 200 Hz 处的双边周期图。
fs = 1000; t = 0:0.001:1-0.001; x = cos(2*pi*100*t)+sin(2*pi*200*t)+randn(size(t)); freq = [100 200]; pxx = periodogram(x,[],freq,fs)
pxx = 1×2
0.2647 0.2313
以下示例说明置信边界与周期图的用法。在周期图中，如果某个频率的置信边界下限超出周围 PSD 估计值的置信边界上限，则清楚地表明时间序列中存在显著的振荡，虽然这不是统计意义的必要条件。
创建一个信号，该信号包含在加性白 N(0,1) 噪声中叠加的 100 Hz 和 150 Hz 正弦波。这两个正弦波的振幅为 1。采样频率为 1 kHz。
fs = 1000; t = 0:1/fs:1-1/fs; x = cos(2*pi*100*t) + sin(2*pi*150*t) + randn(size(t));
获取具有 95% 置信边界的周期图 PSD 估计值。绘制周期图及置信区间，并放大在 100 Hz 和 150 Hz 附近的感兴趣频率区域。
[pxx,f,pxxc] = periodogram(x,rectwin(length(x)),length(x),fs,... 'ConfidenceLevel',0.95); plot(f,10*log10(pxx)) hold on plot(f,10*log10(pxxc),'-.') xlim([85 175]) xlabel('Hz') ylabel('dB/Hz') title('Periodogram with 95%-Confidence Bounds')
紧靠 100 Hz 和 150 Hz 的置信边界下限显著高于 100 Hz 和 150 Hz 以外的置信边界上限。
获取处于加性 噪声中的 100 Hz 正弦波的周期图。数据以 1 kHz 的频率采样。使用 'centered' 选项获取以 DC 为中心的周期图并绘制结果。
fs = 1000;
t = 0:0.001:1-0.001;
x = cos(2*pi*100*t)+randn(size(t));
periodogram(x,[],length(x),fs,'centered')
生成一个由嵌入在高斯白噪声中的 200 Hz 正弦波组成的信号。该信号在 1 kHz 下采样 1 秒。噪声具有方差 0.01²。重置随机数生成器以获得可重现的结果。
rng('default')
Fs = 1000;
t = 0:1/Fs:1-1/Fs;
N = length(t);
x = sin(2*pi*t*200)+0.01*randn(size(t));使用 FFT 计算信号的功率谱，按信号长度归一化。正弦波是分 bin 形式，因此所有功率都集中在单个频率采样中。绘制单边频谱。放大到峰值附近的区域。
q = fft(x,N); ff = 0:Fs/N:Fs-Fs/N; ffts = q*q'/N^2
ffts = 0.4997
ff = ff(1:floor(N/2)+1);
q = q(1:floor(N/2)+1);
stem(ff,abs(q)/N,'*')
axis([190 210 0 0.55])
使用 periodogram 计算信号的功率谱。指定一个汉宁窗和 1024 的 FFT 长度。找出在 200 Hz 处的估计功率与实际值之间的百分比差异。
wind = hann(N); [pun,fr] = periodogram(x,wind,1024,Fs,'power'); hold on stem(fr,pun)
periodogErr = abs(max(pun)-ffts)/ffts*100
periodogErr = 4.7349
重新计算功率谱，但这次使用重排。绘制新估计值，并将其最大值与 FFT 值进行比较。
[pre,ft,pxx,fx] = periodogram(x,wind,1024,Fs,'power','reassigned'); stem(fx,pre) hold off legend('Original','Periodogram','Reassigned')
reassignErr = abs(max(pre)-ffts)/ffts*100
reassignErr = 0.0779
使用 'power' 选项估计在特定频率处正弦波的功率。
创建一个在 1 kHz 下且持续一秒采样的 100 Hz 正弦波。正弦波的振幅为 1.8，等效于功率为 1.8²/2 = 1.62。使用 'power' 选项估计功率。
fs = 1000; t = 0:1/fs:1-1/fs; x = 1.8*cos(2*pi*100*t); [pxx,f] = periodogram(x,hamming(length(x)),length(x),fs,'power'); [pwrest,idx] = max(pxx); fprintf('The maximum power occurs at %3.1f Hz\n',f(idx))
The maximum power occurs at 100.0 Hz
fprintf('The power estimate is %2.2f\n',pwrest)The power estimate is 1.62
生成一个多通道信号的 1024 个采样，该信号包含在加性 高斯白噪声中叠加的三个正弦波。这些正弦波的频率为 、 和 弧度/采样点。使用周期图估计信号的 PSD 并对其绘图。
N = 1024; n = 0:N-1; w = pi./[2;3;4]; x = cos(w*n)' + randn(length(n),3); periodogram(x)
创建一个函数 periodogram_data.m，该函数使用窗返回输入信号的修正周期图功率谱密度 (PSD) 估计值。该函数指定离散傅里叶变换点数等于输入信号的长度。
type periodogram_datafunction [pxx,f] = periodogram_data(inputData,window) %#codegen nfft = length(inputData); [pxx,f] = periodogram(inputData,window,nfft); end
使用 codegen (MATLAB Coder) 生成一个 MEX 函数。
函数中的
%#codegen指令指示 MATLAB® 代码用于代码生成。-args选项指定示例参量，这些参量定义 MEX 文件输入的大小、类和复/实性。对于此示例，将inputData指定为 1024×1 双精度随机向量，将window指定为长度为 1024 的汉明窗。在对 MEX 函数的后续调用中，使用长度为 1024 个采样的输入信号和窗。如果您要使 MEX 函数具有不同名称，请使用
-o选项。如果您要查看代码生成报告，请在
codegen命令的末尾添加-report选项。
codegen periodogram_data -args {randn(1024,1),hamming(1024)}
Code generation successful.
使用周期图函数和您生成的 MEX 函数计算一个长度为 1024 个采样的含噪正弦波的 PSD 估计值。指定正弦波归一化频率为 弧度/采样点和汉宁窗。绘制两个估计值以验证它们是否一致。
N = 1024; x = 2*cos(2*pi/5*(0:N-1)') + randn(N,1); periodogram(x,hann(N)) [pxMex,fMex] = periodogram_data(x,hann(N)); hold on plot(fMex/pi,pow2db(pxMex),':','Color',[0 0.4 0]) hold off grid on legend('periodogram','MEX function')
输入参数
输出参量
详细信息
参考
[1] Auger, François, and Patrick Flandrin. "Improving the Readability of Time-Frequency and Time-Scale Representations by the Reassignment Method." IEEE® Transactions on Signal Processing. Vol. 43, May 1995, pp. 1068–1089.
[2] Fulop, Sean A., and Kelly Fitz. "Algorithms for computing the time-corrected instantaneous frequency (reassigned) spectrogram, with applications." Journal of the Acoustical Society of America. Vol. 119, January 2006, pp. 360–371.
