Main Content

使用 FFT 获得功率频谱密度估计

打开实时脚本

此示例说明如何使用 periodogram 和 fft 函数获得非参数化功率谱密度 (PSD) 估计。这些不同用例说明针对偶数长度输入、归一化频率和以赫兹表示的频率以及单边和双边 PSD 估计，如何正确缩放 fft 的输出。所有用例都使用矩形窗。

此示例重点介绍频率成分不随时间变化的平稳信号。对于频率成分随时间变化的非平稳信号，短时傅里叶变换是一种更好的分析工具。有关详细信息，请参阅Spectrogram Computation with Signal Processing Toolbox。

具有指定采样率的偶数长度输入

对于一个采样率为 1 kHz 的偶数长度信号，分别使用 fft 和 periodogram 获得其周期图。比较二者的结果。

创建一个含 N(0,1) 加性噪声的 100 Hz 正弦波信号。采样频率为 1 kHz。信号长度为 1000 个采样。

fs = 1000;
t = 0:1/fs:1-1/fs;
x = cos(2*pi*100*t) + randn(size(t));

使用 fft 获取周期图。信号是偶数长度的实数值信号。由于信号是实数值信号，您只需要对正负频率之一进行功率估计。为了保持总功率不变，将同时在两组（正频率和负频率）中出现的所有频率乘以因子 2。零频率 (DC) 和奈奎斯特频率不会出现两次。绘制结果。

N = length(x);
xdft = fft(x);
xdft = xdft(1:N/2+1);
psdx = (1/(fs*N)) * abs(xdft).^2;
psdx(2:end-1) = 2*psdx(2:end-1);
freq = 0:fs/length(x):fs/2;

plot(freq,pow2db(psdx))
grid on
title("Periodogram Using FFT")
xlabel("Frequency (Hz)")
ylabel("Power/Frequency (dB/Hz)")

Figure contains an axes object. The axes object with title Periodogram Using FFT, xlabel Frequency (Hz), ylabel Power/Frequency (dB/Hz) contains an object of type line.

计算并使用 periodogram 绘制周期图。二者的结果相同。

periodogram(x,rectwin(N),N,fs)

Figure contains an axes object. The axes object with title Periodogram Power Spectral Density Estimate, xlabel Frequency (Hz), ylabel Power/frequency (dB/Hz) contains an object of type line.

mxerr = max(psdx'-periodogram(x,rectwin(N),N,fs))
mxerr = 
3.4694e-18

具有归一化频率的输入

通过 fft 为使用归一化频率的输入生成周期图。创建一个带 N(0,1) 加性噪声的正弦波信号。该正弦波的角频率为 π/4 弧度/采样点。

N = 1000;
n = 0:N-1;
x = cos(pi/4*n) + randn(size(n));

使用 fft 获取周期图。信号是偶数长度的实数值信号。由于信号是实数值信号，您只需要对正负频率之一进行功率估计。为了保持总功率不变，将同时在两组（正频率和负频率）中出现的所有频率乘以因子 2。零频率 (DC) 和奈奎斯特频率不会出现两次。绘制结果。

xdft = fft(x);
xdft = xdft(1:N/2+1);
psdx = (1/(2*pi*N)) * abs(xdft).^2;
psdx(2:end-1) = 2*psdx(2:end-1);
freq = 0:2*pi/N:pi;

plot(freq/pi,pow2db(psdx))
grid on
title("Periodogram Using FFT")
xlabel("Normalized Frequency (\times\pi rad/sample)")
ylabel("Power/Frequency (dB/(rad/sample))")

Figure contains an axes object. The axes object with title Periodogram Using FFT, xlabel Normalized Frequency ( times pi blank rad/sample), ylabel Power/Frequency (dB/(rad/sample)) contains an object of type line.

计算并使用 periodogram 绘制周期图。二者的结果相同。

periodogram(x,rectwin(N),N)

Figure contains an axes object. The axes object with title Periodogram Power Spectral Density Estimate, xlabel Normalized Frequency ( times pi blank rad/sample), ylabel Power/frequency (dB/(rad/sample)) contains an object of type line.

mxerr = max(psdx'-periodogram(x,rectwin(N),N))
mxerr = 
4.4409e-16

具有归一化频率的复数值输入

使用 fft 为具有归一化频率的复数值输入生成周期图。采用一个带 N(0,1) 复噪声的复指数信号，角频率为 π/4 弧度/采样点。

N = 1000;
n = 0:N-1;
x = exp(1j*pi/4*n) + [1 1j]*randn(2,N)/sqrt(2);

使用 fft 获得周期图。由于输入是复数值，此处求 [0,2π) 弧度/采样点区间内的周期图。绘制结果。

xdft = fft(x);
psdx = (1/(2*pi*N)) * abs(xdft).^2;
freq = 0:2*pi/N:2*pi-2*pi/N;

plot(freq/pi,pow2db(psdx))
grid on
title("Periodogram Using FFT")
xlabel("Normalized Frequency (\times\pi rad/sample)")
ylabel("Power/Frequency (dB/(rad/sample))")

Figure contains an axes object. The axes object with title Periodogram Using FFT, xlabel Normalized Frequency ( times pi blank rad/sample), ylabel Power/Frequency (dB/(rad/sample)) contains an object of type line.

使用 periodogram 获取并绘制周期图。比较 PSD 估计。

periodogram(x,rectwin(N),N,"twosided")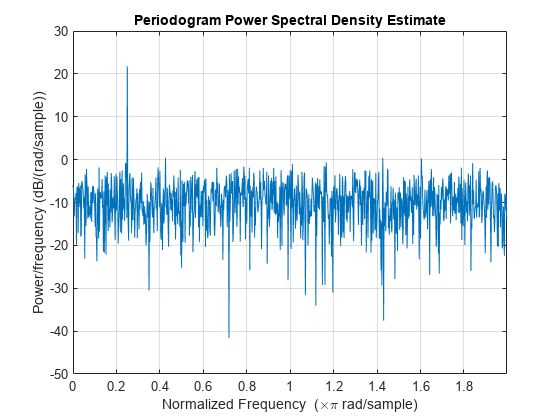

Figure contains an axes object. The axes object with title Periodogram Power Spectral Density Estimate, xlabel Normalized Frequency ( times pi blank rad/sample), ylabel Power/frequency (dB/(rad/sample)) contains an object of type line.

mxerr = max(psdx'-periodogram(x,rectwin(N),N,"twosided"))
mxerr = 
2.2204e-16

另请参阅

App

函数

外部网站