filter 函数

filter 实现为转置的直接 II 型结构，其中 n–1 是滤波器的阶。这是一种具有最少延迟元素的标准形式。

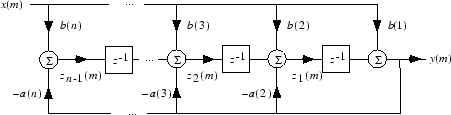
在样本 m 处，filter 计算差分方程

y(m)      =b(1)x(m)+z1(m−1)z1(m)=b(2)x(m)+z2(m−1)−a(2)y(m)     ⋮                    =    ⋮zn−2(m)=b(n−1)x(m)+zn−1(m−1)−a(n−1)y(m)zn−1(m)=b(n)x(m)−a(n)y(m)

在其最基本的形式中，filter 将延迟输出 zi(1) (i = 1, ..., n-1) 初始化为 0。这等效于假设过去的输入和输出都为零。使用 filter 的第四个输入参数设置初始延迟输出，或者使用第二个输出参数获取最终延迟输出：

[y,zf] = filter(b,a,x,zi)

获取初始和最终条件对数据分段滤波非常有用，在内存有所限制时尤其如此。假设您已收集各包含 5000 个数据点的两段数据：

x1 = randn(5000,1);  % Generate two random data sequences.
x2 = randn(5000,1);

可能第一个序列 x1 对应于前 10 分钟的数据，第二个序列 x2 对应于另外 10 分钟的数据。整个序列为 x = [x1;x2]。如果没有足够的内存来容纳合并后的序列，请一次对子序列 x1 和 x2 之一进行滤波。为了确保滤波后的序列的连续性，我们使用来自 x1 的最终条件作为滤波 x2 的初始条件：

[y1,zf] = filter(b,a,x1);
y2 = filter(b,a,x2,zf);

filtic 函数为 filter 生成初始条件。filtic 计算延迟向量，使滤波器的行为反映您指定的过去输入和输出。要使用 filtic 获得与上述相同的输出延迟值 zf，请使用以下代码

zf = filtic(b,a,flipud(y1),flipud(x1));

这对短数据序列滤波非常有用，因为适当的初始条件有助于减少瞬态启动效应。