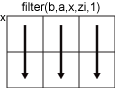
filter
1 维数字滤波器
说明
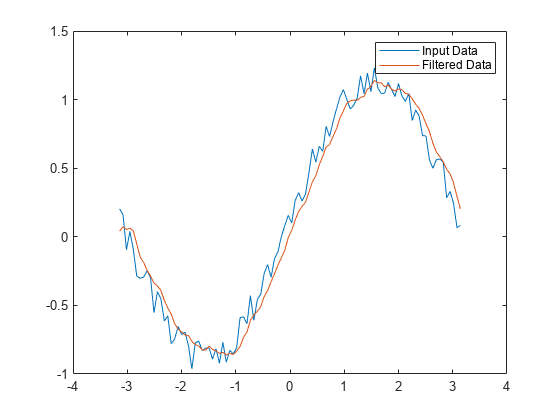
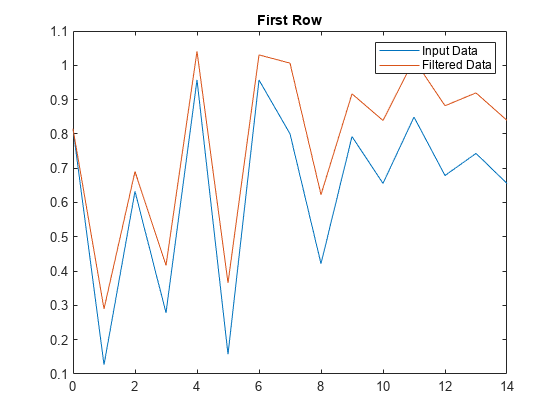
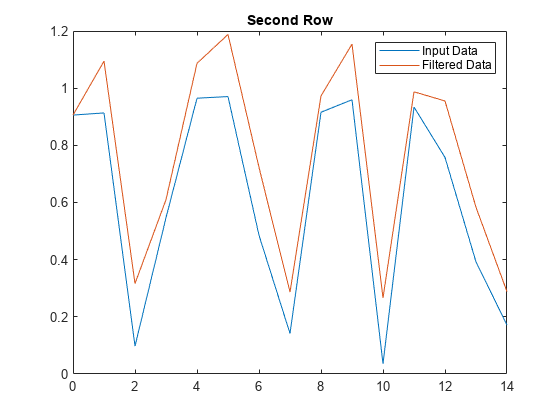
示例
输入参数
输出参量
详细信息
提示
要将
filter函数与来自 FIR 滤波器的b系数结合使用,请使用y = filter(b,1,x)。如果您有 Signal Processing Toolbox™,请将
y = filter(d,x)与digitalFilter(Signal Processing Toolbox) 对象d结合使用来对输入信号x进行滤波。要根据频率响应设定生成d,请使用designfilt(Signal Processing Toolbox)。有关滤波函数的详细信息,请参阅数字滤波 (Signal Processing Toolbox)。
参考
[1] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1999.
扩展功能
版本历史记录
在 R2006a 之前推出