滤波数据
滤波器差分方程
滤波器是一种数据处理技术,可滤掉数据中的高频波动部分使之平滑或从数据中删除特定频率的周期趋势。在 MATLAB® 中,filter 函数会根据以下差分方程对数据 x 的向量进行滤波,该差分方程描述一个抽头延迟线滤波器。
在此方程中,a 和 b 是滤波器系数的向量,Na 是反馈滤波器阶数,Nb 是前馈滤波器阶数。n 是 x 的当前元素的索引。输出 y(n) 是 x 和 y 的当前元素和前面元素的线性组合。
filter 函数使用指定的系数向量 a 和 b 对输入数据 x 进行滤波。有关描述滤波器的差分方程的详细信息,请参阅 [1]。
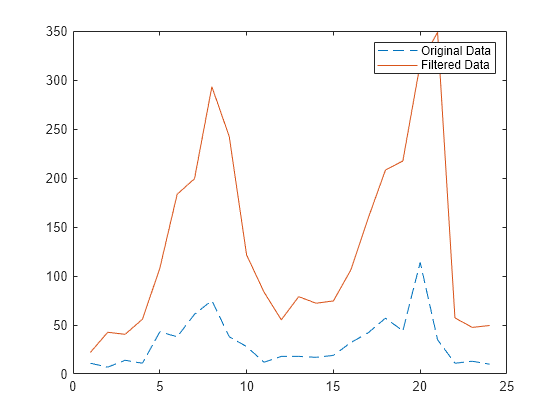
交通流量数据的移动平均滤波器
filter 函数是实现移动平均滤波器的一种方式,它是一种常见的数据平滑技术。
以下差分方程描述一个滤波器,它对关于当前小时和前三个小时的数据的时间相关数据求平均值。
导入描述交通流随时间变化的数据,并将第一列车辆计数赋给向量 x。
load count.dat
x = count(:,1);创建滤波器系数向量。
a = 1; b = [1/4 1/4 1/4 1/4];
计算数据的 4 小时移动平均值,同时绘制原始数据和滤波后的数据。
y = filter(b,a,x); t = 1:length(x); plot(t,x,'--',t,y,'-') legend('Original Data','Filtered Data')

修改数据振幅
此示例显示如何通过应用传递函数来修改数据向量的振幅。
在数字信号处理中,滤波器通常由传递函数表示。以下差分方程的 Z 变换
是以下传递函数。
使用传递函数
修改 count.dat 中数据的振幅。
加载数据并将第一列分配到向量 x。
load count.dat
x = count(:,1);根据传递函数 创建滤波器系数向量。
a = [1 0.2]; b = [2 3];
计算滤波后的数据,同时绘制原始数据和滤波后的数据。此滤波器主要修改原始数据的振幅。
y = filter(b,a,x); t = 1:length(x); plot(t,x,'--',t,y,'-') legend('Original Data','Filtered Data')
参考
[1] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1999.
另请参阅
filter | conv | filter2 | smoothdata | movmean