SimFunctionSensitivity object
SimFunctionSensitivity object, subclass of SimFunction
object
Description
The SimFunctionSensitivity object is a subclass of SimFunction object. It allows you to compute sensitivity.
Syntax
The SimFunctionSensitivity object shares all syntaxes of the
SimFunction object. It has the following additional
syntax.
[T,Y,SensMatrix] = F(___) returns
T, a cell array of numeric vector, Y, a cell
array of 2-D numeric matrices, and SensMatrix, a cell array of 3-D
numeric matrix containing calculated sensitivities of model quantities.
SensMatrix contains a matrix of size
TimePoints x Outputs x
Inputs. TimePoints is the total number of time
points, Outputs is the total number of output factors, and
Inputs is the total number of input factors.
If you specify a single output argument, the object returns an
SimData object or array of SimData objects
with sensitivity information.
Properties
The SimFunctionSensitivity object shares all properties of the
SimFunction object. It has the
following additional properties.
SensitivityOutputs |
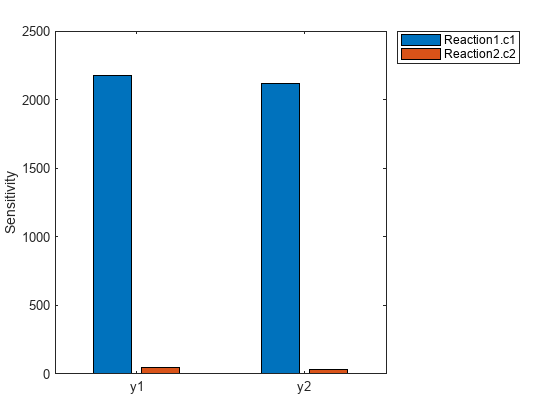
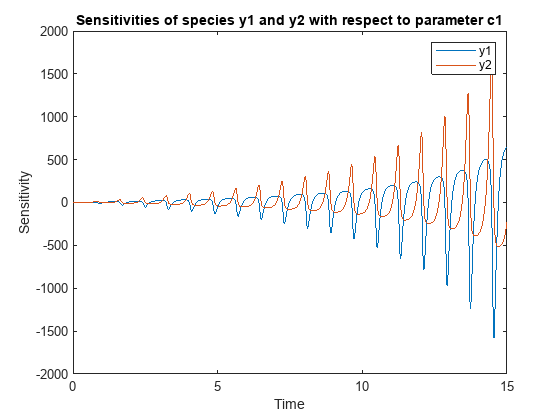
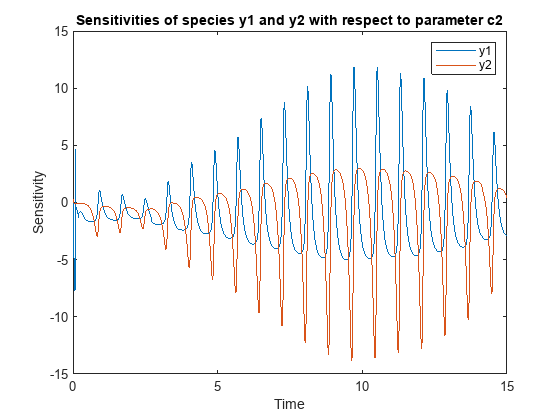
This table contains information about model quantities (species or parameters) for which you want to compute the sensitivities. Sensitivity output factors are the numerators of time-dependent derivatives described in Sensitivity Analysis in SimBiology. This property is read only. |
SensitivityInputs |
This table contains information about model quantities (species, compartments, or parameters) with respect to which you want to compute the sensitivities. Sensitivity input factors are the denominators of time-dependent derivatives described in Sensitivity Analysis in SimBiology. This property is read only. |
SensitivityNormalization | Character vector specifying the normalization method for calculated sensitivities. The following examples show how sensitivities of a species x with respect to a parameter k are calculated for each normalization type.
|
Examples
Version History
Introduced in R2015a
![Figure contains an axes object. The axes object with title States versus Time, xlabel Time, ylabel States contains 6 objects of type line. These objects represent y1, y2, d[y1]/d[Reaction1.c1], d[y2]/d[Reaction1.c1], d[y1]/d[Reaction2.c2], d[y2]/d[Reaction2.c2].](../../examples/simbio/win64/CalculateSensitivitiesUsingSimFunctionSensitivityObjectExample_03.png)