Fuel Cell Equivalent Circuit

Polymer-electrolyte-membrane fuel cell using electrical circuit elements and dynamic membrane water content

Since R2024b

Libraries:
Simscape / Battery / Cells

Description

The Fuel Cell Equivalent Circuit block models a polymer-electrolyte-membrane (PEM) fuel cell by using electrical circuit elements and a dynamic membrane water content model that determines the cell ohmic losses.

The Fuel Cell Equivalent Circuit block models these parts of a fuel cell:

Fuel Cell Potential — Model an ideal PEM fuel cell potential with Tafel equation approximation of losses.
Fuel Cell Dynamic Overpotential — Model the dynamic overpotential contributions of the fuel cell.
Fuel Cell Membrane — Model the water content dynamics.

Fuel Cell Potential

The block models ideal PEM fuel cell potential by approximating the losses using the Tafel equation:

$E = E_{o c} - A \cdot \ln (\frac{I}{I_{0}}) .$

In this equation:

E_OC is the nominal potential and is equal to the value of the Open-circuit voltage parameter.
A is the value of the Tafel slope parameter, in volts.
I₀ is the value of the Nominal exchange current parameter, in Amperes.
I is the current drawn from the fuel cell, in Amperes.

Fuel Cell Dynamic Overpotential

The block models the dynamic overpotential contributions of the fuel cell:

$\frac{1}{R_{d}} (τ \frac{d v_{d}}{d t} + v_{d}) = I .$

In this equation:

τ is the value of the Overpotential time constant parameter, in seconds.
R_d is the value of the Activation and concentration equivalent resistance parameter, in ohms.
v_d is the voltage drop that accounts for the fuel cell dynamics.

Fuel Cell Membrane

The block models the ohmic resistance dynamics of a fuel cell membrane by discretizing the membrane thickness into slices, from the anode to the cathode. The net molar flow of the water through each slice determines the local water content and, consequently, the local resistance to the proton flow. The block computes the total membrane ohmic resistance by summing all slice resistances.

This figure describes a control volume analysis of a thin element of a fuel cell membrane:

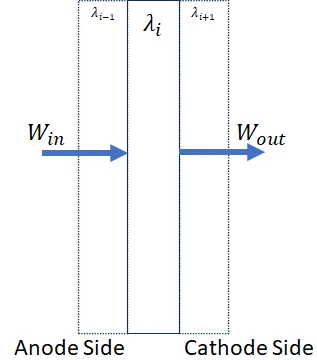
Control volume analysis of a thin element of a fuel cell membrane. On the left, W_in represents the molar flow rate, in mol/s, of the water molecules that flow into the membrane slice. On the right, W_out represents the molar flow rate, in mol/s of the water molecules that flow out of the slice control volume.

The block applies the law of conservation of mass to generate the governing equation of the water content inside the ith membrane slice,

$α \frac{d λ_{i}}{d t} = W_{i n} - W_{o u t,}$

where:

W_in is the molar flow rate, in mol/s, of the water molecules that flow into the membrane slice.
W_out is the molar flow rate, in mol/s of the water molecules that flow out of the slice control volume.
λ_i is a nondimensional value that captures the local water concentration relative to the membrane material. The accumulated water is proportional to the net molar flow of the water through the membrane slice.

In this equation, α is a constant equal to

$α = \frac{S \cdot \frac{δ}{N} \cdot ρ}{Μ},$

where:

S is the value of the Active surface area parameter.
δ/N is the slice thickness. δ is the value of the Total membrane thickness parameter. N is the value of the Number of membrane discretizations parameter.
ρ is the value of the Dry density of material parameter.
Μ is the value of the Molecular mass of material parameter.

Diffusion and electro-osmotic drag are the two key mechanisms for water transportation through a fuel cell membrane. A hydrogen fuel cell generates water molecules at the cathode and, through a diffusion mechanism, the molecules of water diffuse over towards the anode side of the membrane. The electro-osmotic drag transfers the water molecules from the anode side to the cathode side of the membrane. While the diffusion mechanisms can be bidirectional between the anode and the cathode, the electro-osmotic drag causes the molecules of water to flow only from the anode to the cathode.

These equations describe the diffusion and electro-osmotic drag mechanisms:

$\begin{array}{l} W_{d r a g} = κ_{1} G I λ \\ W_{d i f f} = κ_{2} D \frac{d λ}{d z} \end{array}$

In these equations:

dz refers to a length into the membrane, measured from the anode or membrane interface.
dλ represents the difference of water content across a membrane length of dz.
G is the electro-osmotic drag coefficient. To specify this value, set the Interface for electro-osmotic drag parameters parameter to:
- Mask Parameters — G is a constant and is equal to the value of the Electro-osmotic drag coefficient parameter.
- Lookup table — The block calculates the value of G by using the value of the Drag table data (1-D) and Electro-osmotic drag coefficient breakpoints parameters. The values of the lookup table are based on the average membrane water content.
- Literature Heuristic — The block controls G by using literature heuristic and the value of the Drag scale factor parameter.
D is the diffusion coefficient. To specify this value, set the Interface for diffusion parameters parameter to:
- Mask Parameters — D is a constant and is equal to the value of the Diffusion coefficient parameter.
- Lookup table — The block calculates the value of D by using the value of the Diffusion coefficient table data (1-D) and Diffusion coefficient breakpoints parameters. The values of the lookup table are based on the temperature.
- Literature Heuristic — The block controls D by using an empirical function derived from experiments.
$κ_{1} = \frac{1}{22 F},$ where F is the Faraday constant in S*A/mol.
$κ_{2} = \frac{S \cdot ρ}{Μ \cdot \frac{δ}{N}} .$

The block considers the full membrane thickness as a series of linked slices with the appropriate and respective boundary conditions. At the ith slice, the block considers the water molar inflow and outflow as contributions from the two water transport mechanisms. The block assumes that these two mechanisms independently contribute to the water molar mass flow:

$\begin{array}{l} W_{i n} = W_{d r a g, i n} + W_{d i f f, i n} \\ W_{o u t} = W_{d r a g, o u t} + W_{d i f f, o u t} \end{array}$

For a generic membrane slice i of δ/N thickness, the block assumes that:

The molecules of water that enter the i slice due to electro-osmotic drag are equal to the molecules of water that leave the i-1 slice due to electro-osmotic drag.
The molecules of water that exit the i slice due to electro-osmotic drag are equal to:

$\begin{array}{l} W_{d r a g, o u t, i} = κ_{1} G I λ_{i} \\ W_{d r a g, i n, i} = W_{d r a g, o u t, i - 1} \end{array}$
The molecules of water that enter and exit the i slice due to diffusion are equal to:

$\begin{array}{l} W_{d i f f, o u t, i} = κ_{2} D \frac{λ_{i} - λ_{i + 1}}{\frac{δ}{N}} \\ W_{d i f f, i n, i} = κ_{2} D \frac{λ_{i - 1} - λ_{i}}{\frac{δ}{N}} \end{array}$
The current I is constant for all membrane slices. The proton flow is strictly in plane and is equal in each slice.

By solving the dynamic systems for λ_i, the block determines the conductivity σ, in S/m, by evaluating this equation for each slice:

$σ = (0.005139 λ - 0.00326) e^{1268 (\frac{1}{303.15} - \frac{1}{T})},$

where T is the temperature, in Kelvin. You can convert each slice conductivity into slice resistance. The total membrane resistance is equal to the sum of the resistance of each slice.

Boundary Conditions

The fuel cell membrane model considers the water content dynamics for a discrete slice of the membrane. The block must also consider the environment at the outer edges of the membrane. To establish the boundary conditions of the entire membrane, the block assumes that:

At the anode side, the water molar inflow is due to diffusion only.
At the cathode side, the water molar outflow is due to both the electro-osmotic drag and diffusion.

To set the boundary conditions of the membrane, set the Interface for lambda boundary conditions parameter to one of these options:

Mask Parameters — Specify the values of the boundary conditions directly by using the Anode water content and Cathode water content parameters.
Physical Signal Inputs — Control the boundary conditions externally using the Anode water content and Cathode water content input ports.

Examples

New

Model PEM Fuel Cell with Membrane Water Dynamics

Model a proton-exchange membrane (PEM) fuel cell stack with a custom Simscape™ block. The block models the water transport dynamics that occur in the membrane electrode assembly (MEA) of a PEM fuel cell. For more information about the water transport dynamics, see the Fuel Cell Equivalent Circuit block.

Since R2024b
Open Script

Ports

Input

expand all

Anode water content — Water content in anode, unitless
physical signal

Physical signal input port associated with the water content in the anode.

Dependencies

To enable this port, in the Membrane settings, set Interface for lambda boundary conditions to Physical Signal Inputs.

Cathode water content — Water content in cathode, unitless
physical signal

Physical signal input port associated with the water content in the cathode.

Dependencies

To enable this port, in the Membrane settings, set Interface for lambda boundary conditions to Physical Signal Inputs.

Cell temperature — Cell temperature, K
physical signal

Physical signal input port associated with the cell temperature.

Dependencies

To enable this port, in the Thermal settings, set Interface for temperature to Physical Signal Inputs.

Conserving

expand all

+ — Fuel cell positive terminal
electrical

Electrical conserving port associated with the positive terminal of the fuel cell.

- — Fuel cell negative terminal
electrical

Electrical conserving port associated with the negative terminal of the fuel cell.

Parameters

expand all

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Main

Active surface area — Total surface area of active cell
`14.8` `cm^2` (default) | positive scalar

Total surface area of the active cell.

Open-Circuit Voltage

Open-circuit voltage — Open-circuit voltage
`1.23` `V` (default) | nonnegative scalar

Open-circuit voltage. The block uses this value to calculate the potential of an ideal PEM fuel cell.

Terminal voltage operating range, [Min Max] — Operating range of terminal voltage
`[0, inf]` `V` (default) | vector of two nonnegative scalars

Operating range of the terminal voltage.

Overpotential

Tafel slope — Tafel slope
`0.0136` `V` (default) | nonnegative scalar

Tafel slope. The block uses this value to calculate the potential of an ideal PEM fuel cell.

Nominal exchange current — Nominal exchange current
`0.04777` `A` (default) | positive scalar

Nominal exchange current. The block uses this value to calculate the potential of an ideal PEM fuel cell.

Activation and concentration equivalent resistance — Activation and concentration equivalent resistance
`5e-3` `Ohm` (default) | positive scalar

Activation and concentration equivalent resistance. The block uses this value to model the dynamic overpotential contributions of the fuel cell.

Overpotential time constant — Overpotential time constant
`100` `s` (default) | positive scalar

Overpotential time constant. The block uses this value to model the dynamic overpotential contributions of the fuel cell.

Membrane

Total membrane thickness — Total thickness of membrane
`0.127` `mm` (default) | positive scalar

Total thickness of the membrane.

Dry density of material — Dry density of membrane material
`19` `g/cm^3` (default) | positive scalar

Dry density of the membrane material.

Molecular mass of material — Molecular mass of the material
`1400` `g/mol` (default) | positive scalar

Molecular mass of the membrane material.

Number of membrane discretizations — Number of membrane discretizations
`3` (default) | positive scalar

Number of membrane discretizations. The value of this parameter specifies the number of slices you divide the membrane into.

Interface for lambda boundary conditions — Option for lambda boundary conditions
`Mask Parameters` (default) | `Physical Signal Inputs`

Specify the lambda boundary conditions as mask parameters or physical signal inputs.

Anode water content — Water content in anode
`1` (default) | nonnegative scalar

Water content in the anode.

Dependencies

To enable this parameter, set Interface for lambda boundary conditions to Mask Parameters.

Cathode water content — Water content in cathode
`1` (default) | nonnegative scalar

Water content in the cathode.

Dependencies

To enable this parameter, set Interface for lambda boundary conditions to Mask Parameters.

Initial lambda of each slice — Initial lambda of each slice
`1` (default) | nonnegative scalar

Initial value of lambda of each slice.

Interface for diffusion parameters — Option for diffusion parameters
`Mask Parameters` (default) | `Lookup table` | `Literature Heuristic`

Specify the lambda boundary conditions as mask parameters, lookup tables, or with literature heuristic.

Diffusion coefficient — Diffusion coefficient
`1.5e-10` `m^2/s` (default) | positive scalar

Diffusion coefficient.

Dependencies

To enable this parameter, set Interface for diffusion parameters to Mask Parameters.

Diffusion coefficient table data (1-D) — Diffusion coefficient table data
`[1e-10, 1.5e-10]` `m^2/s` (default) | vector of positive scalars

Lookup table data for diffusion coefficient. The value of this parameter must be a vector of at least two positive scalars. The number of elements of this vector must be equal to the number of elements of the Diffusion coefficient breakpoints parameter value.

Dependencies

To enable this parameter, set Interface for diffusion parameters to Lookup table.

Diffusion coefficient breakpoints — Breakpoints for diffusion coefficient lookup table
`[0, 400]` `K` (default) | vector of nonnegative scalars

Breakpoints for the lookup table data of the diffusion coefficient. The value of this parameter must be a vector of at least two strictly ascending nonnegative scalars. The number of elements of this vector must be equal to the number of elements of the Diffusion coefficient table data (1-D) parameter value.

Dependencies

To enable this parameter, set Interface for diffusion parameters to Lookup table.

Interface for electro-osmotic drag parameters — Option for electro-osmotic drag parameters
`Mask Parameters` (default) | `Lookup table` | `Literature Heuristic`

Specify the lambda boundary conditions as mask parameters, lookup tables, or with literature heuristic.

Electro-osmotic drag coefficient — Electro-osmotic drag coefficient
`2.5` (default) | positive scalar

Electro-osmotic drag coefficient.

Dependencies

To enable this parameter, set Interface for electro-osmotic parameters to Mask Parameters.

Drag table data (1-D) — Drag table data
`[1, 2.5, 2.5]` (default) | vector of nonnegative scalars

Lookup table data for drag. The value of this parameter must be a vector of at least two nonnegative scalars. The number of elements of this vector must be equal to the number of elements of the Electro-osmotic drag coefficient breakpoints parameter value.

Dependencies

To enable this parameter, set Interface for electro-osmotic parameters to Lookup table.

Electro-osmotic drag coefficient breakpoints — Breakpoints for drag coefficient lookup table
`[1, 14, 20]` (default) | vector of nonnegative scalars

Breakpoints for the lookup table data of drag coefficients. The value of this parameter must be a vector of at least two strictly ascending scalars. The number of elements of this vector must be equal to the number of elements of the Drag table data (1-D) parameter value.

Dependencies

To enable this parameter, set Interface for electro-osmotic parameters to Lookup table.

Drag scale factor — Drag scale factor
`1` (default) | positive scalar

Drag scale factor. The value scales the heuristic equation that the block uses to model the electro-osmotic drag depending on water content.

Dependencies

To enable this parameter, set Interface for electro-osmotic parameters to Literature Heuristic.

Thermal

Interface for temperature — Option for temperature parameter
`Mask Parameters` (default) | `Physical Signal Inputs`

Specify the cell temperature as mask parameters or physical signal inputs.

Cell temperature — Temperature of fuel cell
`303.15` `K` (default) | positive scalar

Temperature of the fuel cell.

Dependencies

To enable this parameter, set Interface for temperature to Mask Parameters.

References

[1] Zhou, Daming, Fei Gao, Elena Breaz, Alexandre Ravey, Abdellatif Miraoui, and Ke Zhang. "Dynamic Phenomena Coupling Analysis and Modeling of Proton Exchange Membrane Fuel Cells." IEEE Transactions on Energy Conversion 31, no. 4 (December 2016): 1399–1412. https://doi.org/10.1109/TEC.2016.2587162.

[2] Wu, Hao, Peter Berg, and Xianguo Li. "Non-Isothermal Transient Modeling of Water Transport in PEM Fuel Cells." Journal of Power Sources 165, no. 1 (2007): 232–43. https://doi.org/10.1016/j.jpowsour.2006.11.061.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2024b

Fuel Cell Equivalent Circuit

Description

Fuel Cell Potential

Fuel Cell Dynamic Overpotential

Fuel Cell Membrane

Examples

Model PEM Fuel Cell with Membrane Water Dynamics

Ports

Input

Anode water content — Water content in anode, unitless physical signal

Dependencies

Cathode water content — Water content in cathode, unitless physical signal

Dependencies

Cell temperature — Cell temperature, K physical signal

Dependencies

Conserving

+ — Fuel cell positive terminal electrical

- — Fuel cell negative terminal electrical

Parameters

Main

Active surface area — Total surface area of active cell 14.8 cm^2 (default) | positive scalar

Open-Circuit Voltage

Open-circuit voltage — Open-circuit voltage 1.23 V (default) | nonnegative scalar

Terminal voltage operating range, [Min Max] — Operating range of terminal voltage [0, inf] V (default) | vector of two nonnegative scalars

Overpotential

Tafel slope — Tafel slope 0.0136 V (default) | nonnegative scalar

Nominal exchange current — Nominal exchange current 0.04777 A (default) | positive scalar

Activation and concentration equivalent resistance — Activation and concentration equivalent resistance 5e-3 Ohm (default) | positive scalar

Overpotential time constant — Overpotential time constant 100 s (default) | positive scalar

Membrane

Total membrane thickness — Total thickness of membrane 0.127 mm (default) | positive scalar

Dry density of material — Dry density of membrane material 19 g/cm^3 (default) | positive scalar

Molecular mass of material — Molecular mass of the material 1400 g/mol (default) | positive scalar

Number of membrane discretizations — Number of membrane discretizations 3 (default) | positive scalar

Interface for lambda boundary conditions — Option for lambda boundary conditions Mask Parameters (default) | Physical Signal Inputs

Anode water content — Water content in anode 1 (default) | nonnegative scalar

Dependencies

Cathode water content — Water content in cathode 1 (default) | nonnegative scalar

Dependencies

Initial lambda of each slice — Initial lambda of each slice 1 (default) | nonnegative scalar

Interface for diffusion parameters — Option for diffusion parameters Mask Parameters (default) | Lookup table | Literature Heuristic

Diffusion coefficient — Diffusion coefficient 1.5e-10 m^2/s (default) | positive scalar

Dependencies

Diffusion coefficient table data (1-D) — Diffusion coefficient table data [1e-10, 1.5e-10] m^2/s (default) | vector of positive scalars

Dependencies

Diffusion coefficient breakpoints — Breakpoints for diffusion coefficient lookup table [0, 400] K (default) | vector of nonnegative scalars

Dependencies

Interface for electro-osmotic drag parameters — Option for electro-osmotic drag parameters Mask Parameters (default) | Lookup table | Literature Heuristic

Electro-osmotic drag coefficient — Electro-osmotic drag coefficient 2.5 (default) | positive scalar

Dependencies

Drag table data (1-D) — Drag table data [1, 2.5, 2.5] (default) | vector of nonnegative scalars

Dependencies

Electro-osmotic drag coefficient breakpoints — Breakpoints for drag coefficient lookup table [1, 14, 20] (default) | vector of nonnegative scalars

Dependencies

Drag scale factor — Drag scale factor 1 (default) | positive scalar

Dependencies

Thermal

Interface for temperature — Option for temperature parameter Mask Parameters (default) | Physical Signal Inputs

Cell temperature — Temperature of fuel cell 303.15 K (default) | positive scalar

Dependencies

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

See Also

Anode water content — Water content in anode, unitless
physical signal

Cathode water content — Water content in cathode, unitless
physical signal

Cell temperature — Cell temperature, K
physical signal

+ — Fuel cell positive terminal
electrical

- — Fuel cell negative terminal
electrical

Active surface area — Total surface area of active cell
`14.8` `cm^2` (default) | positive scalar

Open-circuit voltage — Open-circuit voltage
`1.23` `V` (default) | nonnegative scalar

Terminal voltage operating range, [Min Max] — Operating range of terminal voltage
`[0, inf]` `V` (default) | vector of two nonnegative scalars

Tafel slope — Tafel slope
`0.0136` `V` (default) | nonnegative scalar

Nominal exchange current — Nominal exchange current
`0.04777` `A` (default) | positive scalar

Activation and concentration equivalent resistance — Activation and concentration equivalent resistance
`5e-3` `Ohm` (default) | positive scalar

Overpotential time constant — Overpotential time constant
`100` `s` (default) | positive scalar

Total membrane thickness — Total thickness of membrane
`0.127` `mm` (default) | positive scalar

Dry density of material — Dry density of membrane material
`19` `g/cm^3` (default) | positive scalar

Molecular mass of material — Molecular mass of the material
`1400` `g/mol` (default) | positive scalar

Number of membrane discretizations — Number of membrane discretizations
`3` (default) | positive scalar

Interface for lambda boundary conditions — Option for lambda boundary conditions
`Mask Parameters` (default) | `Physical Signal Inputs`

Anode water content — Water content in anode
`1` (default) | nonnegative scalar

Cathode water content — Water content in cathode
`1` (default) | nonnegative scalar

Initial lambda of each slice — Initial lambda of each slice
`1` (default) | nonnegative scalar

Interface for diffusion parameters — Option for diffusion parameters
`Mask Parameters` (default) | `Lookup table` | `Literature Heuristic`

Diffusion coefficient — Diffusion coefficient
`1.5e-10` `m^2/s` (default) | positive scalar

Diffusion coefficient table data (1-D) — Diffusion coefficient table data
`[1e-10, 1.5e-10]` `m^2/s` (default) | vector of positive scalars

Diffusion coefficient breakpoints — Breakpoints for diffusion coefficient lookup table
`[0, 400]` `K` (default) | vector of nonnegative scalars

Interface for electro-osmotic drag parameters — Option for electro-osmotic drag parameters
`Mask Parameters` (default) | `Lookup table` | `Literature Heuristic`

Electro-osmotic drag coefficient — Electro-osmotic drag coefficient
`2.5` (default) | positive scalar

Drag table data (1-D) — Drag table data
`[1, 2.5, 2.5]` (default) | vector of nonnegative scalars

Electro-osmotic drag coefficient breakpoints — Breakpoints for drag coefficient lookup table
`[1, 14, 20]` (default) | vector of nonnegative scalars

Drag scale factor — Drag scale factor
`1` (default) | positive scalar

Interface for temperature — Option for temperature parameter
`Mask Parameters` (default) | `Physical Signal Inputs`

Cell temperature — Temperature of fuel cell
`303.15` `K` (default) | positive scalar

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.