分析钒液流电池的性能

自 R2023b 起

此示例说明了如何对钒氧化还原流动电池 (VRFB) 进行建模、计算荷电状态 (SOC) 以及评估电解质流量对电池性能的影响。

构建 VFRB 模型

VRFB（可逆式热泵）在电网应用的能源存储领域正迅速普及，这得益于其长寿命、易于维护以及对环境影响较小的优势。在此示例中，通过求解常微分方程 (ODE) 并使用 Simscape™ 自定义组件来对 VRFB 进行建模。为了确定电池性能，您需要计算电解槽和电池堆中的四种钒元素的物质平衡方程式。等效电路模型描述了电池的电响应。

定义数学模型

下图显示了 VRFB 的示意图。电池由串联连接的电池电芯堆叠而成，并配有从大型电解槽中补充的电解质。电池组及其泵系统安装在两个电解质储槽上方。在 VRFB 中，钒存在于四种不同的价态。在电极上的钒离子状态发生变化时，电芯堆会释放出电子，这些电子通过外部电路流动。这些电子构成了电路中的直流电流。为了增加电池容量，请增加电解槽的大小。要增加电池的功率，请增加电池组中的电芯数量。

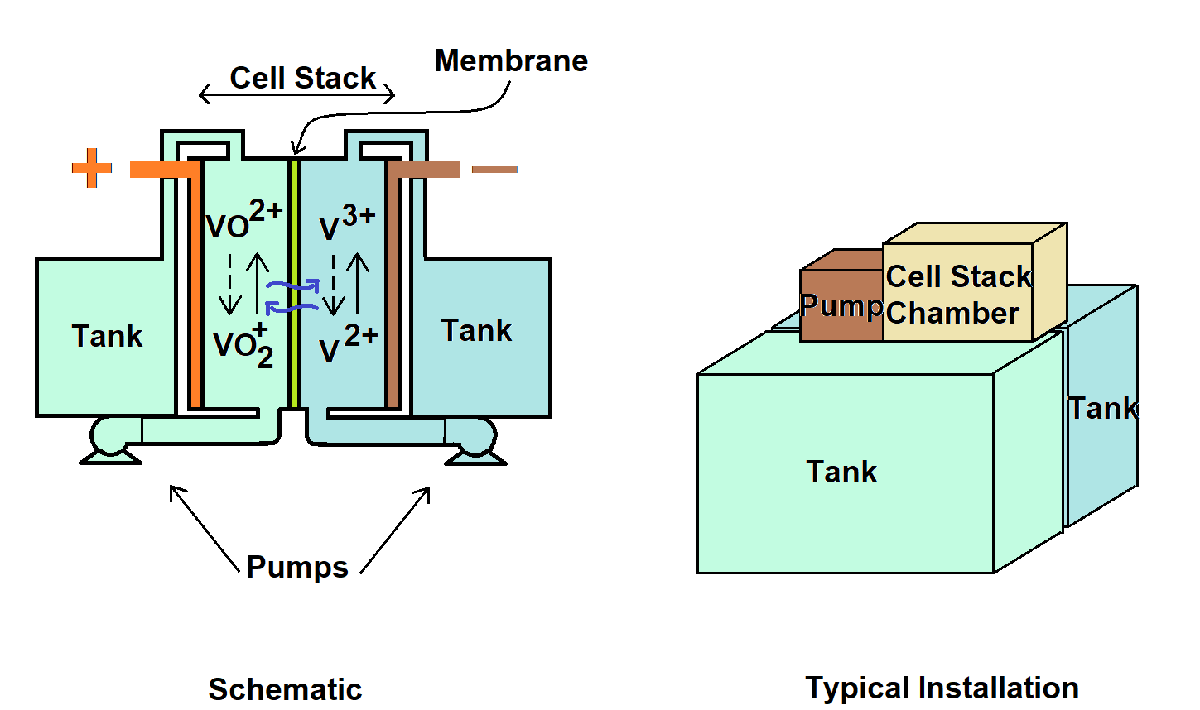
该电化学反应定义了阴极上的反应：

${VO}^{2 +} + H_{2} O ⟷ {VO}_{2}^{+} + {2 H}^{+} + e^{-}, E_{+} ~ 1 V$ .

该电化学反应定义了阳极上的反应：

$V^{3 +} + e^{-} ⟷ V^{2 +}, E_{-} ~ - 0.3 V$ .

该方程式描述了电芯堆中四种钒元素的质量平衡：

$U_{cell} \frac{d c_{i}^{cell}}{dt} = \frac{Q}{N_{s}} (c_{i}^{tank} - c_{i}^{cell}) \pm \frac{I}{nF} - \frac{A_{m}}{t_{m}} f (\sum_{}^{} D_{i} c_{i}),$

其中：

$i$ 表示四种不同的钒化合态（价态分别为 2、3、4 和 5）。
$c_{i}^{cell}$ 和 $c_{i}^{tank}$ 分别表示电芯堆和电解槽中钒离子 $i$ 的浓度。
$I$ 是电流。
$Q$ 是电解质流量。
$N_{s}$ 是堆叠中串联电芯的数量。
$U_{cell}$ 是单电芯体积。
$A_{m}$ 是电芯膜的面积。
$t_{m}$ 是电芯膜的厚度。
$D_{i}$ 是钒化合物 $i$ 通过膜的扩散系数。

符号 $\pm$ 位于术语 $\frac{I}{F}$ 之前时，对钒的第 2 和第 5 种同位素表示正值，对第 3 和第 4 种同位素表示负值。在此情况下， $n$ 等于 1。方程左侧 (LHS) 描述了电芯中物质浓度随时间的变化率。方程右侧 (RHS) 的第一项代表电解质流动导致的活性物质浓度变化。右边项的第二个项表示电荷的流动。右侧的第三项代表钒元素在扩散系数和元素浓度[1,2]的函数下穿过膜的迁移。

该方程式描述了电解槽中四种钒的质量平衡：

$U_{tank} \frac{d c_{i}^{tank}}{dt} = Q (c_{i}^{cell} - c_{i}^{tank}),$

其中：

$i$ 表示四种不同的钒化合价态（化合价为 2、3、4 和 5）。
$c_{i}^{cell}$ 和 $c_{i}^{tank}$ 分别表示电芯堆和电解槽中钒离子 $i$ 的浓度。
$Q$ 是电解质流量。
$U_{tank}$ 是电解槽的体积。

电阻器-电容器对（RC 对）等效电路模型代表了电芯的电动态特性。

该方程式定义了电芯的开路电势：

$V_{oc} = V_{elecPot} + \frac{RT}{nF} \log (\frac{{SOC}_{p}}{1 - {SOC}_{p}} . \frac{{SOC}_{n}}{1 - {SOC}_{n}}),$

其中：

$V_{elecPot}$ 表示电极电势，其由以下关系式给出： $E_{+} - E_{-} ~ 1.3 V$ 。
$R$ 是普适气体常数。
$T$ 是电池的温度。
$F$ 是法拉第常数。
$n$ 等于 1。
${SOC}_{p} = \frac{c_{5}^{tank}}{c_{4}^{tank} + c_{5}^{tank}} .$
${SOC}_{n} = \frac{c_{2}^{tank}}{c_{2}^{tank} + c_{3}^{tank}} .$

构建自定义组件

vanadiumRedoxFlowBattery SSC 文件中的自定义组件实现了数学模型。电芯堆和电解槽的变量分别以 cell 和 tank 为前缀。电芯堆叠浓度是一个向量，其长度等于串联电芯的数量。每个电芯的电解质流量因液压情况而异。正半电芯流量分布不均和负半电芯流量分布不均参数定义了堆叠中每个电芯的电解质流量。槽浓度是一个标量值，以立方米为单位指定。SOC 基于电解槽中的活性物质浓度。

自定义组件有一个正电极和一个负电极。自定义组件还以泵流量 $Q$ 作为输入。您可以指定正极和负极半电芯的流量。如果流量较低，即使电解槽中的活性物质足够，电芯堆也会迅速耗尽所有钒元素。因此，您必须指定合理的电解质流量。

您可以使用 Probe 模块可视化所有变量，包括不同活性物质浓度和电池 SOC。电池等效电路模型使用以下代码确定电池电压：

voltNernstEqn == V0 + (R*temperature/F)*log(SOCp*SOCn/((1-SOCp)*(1-SOCn)));
voltOhmic == i*ecmR0;
i*ecmR1 == ecmTau1*voltDynamic.der + voltDynamic;
v == Ns*voltNernstEqn + voltOhmic + voltDynamic;

这里，v 是电池电压，等于能斯特方程中的开路电势 voltNernstEqn、由于欧姆电阻引起的电压降 voltOhmic 以及 RC 电路两端电压降 voltDynamic 的总和。

配置模型

VRFBperformanceAnalysis SLX 文件显示了连接到模拟简单负载的电阻器的 VRFB 自定义组件。流量模块定义了两个泵的恒定流量。

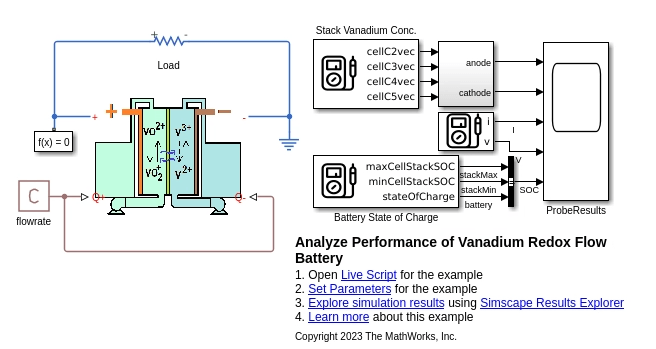
vrfbPerformanceAnalysisParams.m 文件定义了 VRFB 模型的参数。要更改模型参数，在 MATLAB® 命令行窗口中，输入以下命令：

edit vrfbPerformanceAnalysisParams.m

参数 flowrate_lpm 定义电池中电解质的恒定输入流量。电池由 10 个串联的电芯组成。要确定电池中串联的电池电芯数量，请使用圆点表示法 (elec.Ns) 查询 elec 结构中的 Ns 字段。chem 和 hydr 结构分别定义了电池的化学和水力参数。此例使用钒浓度为 2M 的电解质。参数 hydr.FlowMalDistrPos 和 hydr.FlowMalDistrPos 是单位向量，表示电池组沿电池堆没有流分布不均。

设置模型参数

电气

elec.Ns - 电池组中串联的电芯数量，指定为正整数。
elec.V0 - 单电芯电极电势，以伏特为单位，指定为标量。
elec.R0 - 电池的电阻值，单位为欧姆，指定为标量。
elec.R1 - 电池 RC 电路的总电阻，单位为欧姆，指定为标量。
elec.Tau1 - 电池 RC 电路的时间常数，单位为秒，指定为标量。
elec.SOC - 初始电池 SOC，指定为范围 [0,1] 内的标量。

化学

chem.Len - 多孔电极的长度，单位为米，指定为正标量。
chem.Wid - 多孔电极的宽度，单位为米，指定为正标量。
chem.Thk - 多孔电极的厚度，单位为米，指定为正标量。
chem.Por - 电极孔隙率，指定为 [0,1] 范围内的标量。
chem.Mem - 膜厚度，单位为米，指定为正标量。
chem.M - 电解质溶液中的钒摩尔浓度，以摩尔/升为单位，指定为标量。
chem.D2、D3、D4、D5 - 钒活性物质 $V^{2 +}$ 、 $V^{3 +}$ 、 ${VO}^{2 +}$ 、 ${VO}_{2}^{+}$ 通过膜的扩散系数，以 $m^{2}$ /s 为单位，指定为标量值。

液压

hydr.TankVol - 储液槽体积，单位为 $m^{3}$ ，指定为正标量。
hydr.FlowMalDistrPos - 电解质流入正极时沿电池堆的流分布不均，指定为一个向量，其长度等于电池堆中的电芯数量。
hydr.FlowMalDistrNeg - 电解质流入负极时沿电池堆的流分布不均，指定为一个向量，其长度等于电池堆中的电芯数量。

此示例对堆叠中的所有电芯进行均匀流建模。要建模流分配不均的示例，在 MATLAB® 命令行窗口中，输入以下命令：

elec.Ns = 10;
hydr.FlowMalDistrPos = [1.04 1.03 1.02 1.01 1.00 1.00 0.99 0.98 0.97 0.96]; 
hydr.FlowMalDistrNeg = hydr.FlowMalDistrPos;

热

温度 - 电池的工作温度，单位为开尔文，指定为正标量。

flowrate_lpm 和 systemLoad 参数分别定义电解质流量（以升/分钟为单位）和系统负载的外部电阻（以欧姆为单位）。

运行模型

将电池的初始 SOC elec.SOC 设置为 1。设置模型参数。

run("vrfbPerformanceAnalysisParams.m");

定义堆叠中电芯的数量。

elec.Ns = 10;

定义需要评估电池的恒定流量值。

flowrateVec = [0 0.5 1 15 30];

对所有流量值运行仿真。

numCase = length(flowrateVec);
simRes  = cell(1,numCase);
for itr = 1:numCase
    flowrate_lpm = flowrateVec(1,itr);
    sim("VRFBperformanceAnalysis.slx");
    simRes{1,itr} = simlog_vrfbResults;
end

绘制仿真结果

绘制不同流量下 VRFB 的电流、电压和 SOC 值。在无流量（流量为 0 LPM）的情况下，电池会提供电流，直到电池堆中的活性物质发生反应释放电子为止。一旦电池组电芯的电量耗尽，即使电池盒中仍含有活性物质，电流也会停止流动，电池 SOC 也会显示为 0。随着流量的增加，电芯堆中的反应物反应速度下降，但被电解质从储槽中带入的新鲜反应物抵消了这一下降。在此示例中，15 LPM 是一个合理的流量，可确保堆栈反应物以与整体电池 SOC 或槽反应物比例一致的速度减少。

for itr = 1:numCase
    vrfbPlotAnalysisResults(simRes{1,itr});
end

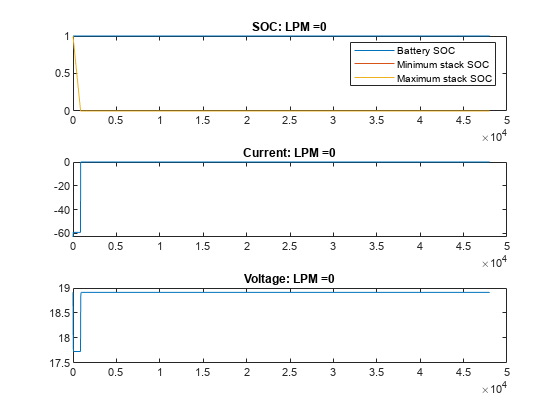
Figure VRFB: LPM =0 contains 3 axes objects. Axes object 1 with title SOC: LPM =0 contains 3 objects of type line. These objects represent Battery SOC, Minimum stack SOC, Maximum stack SOC. Axes object 2 with title Current: LPM =0 contains an object of type line. Axes object 3 with title Voltage: LPM =0 contains an object of type line.

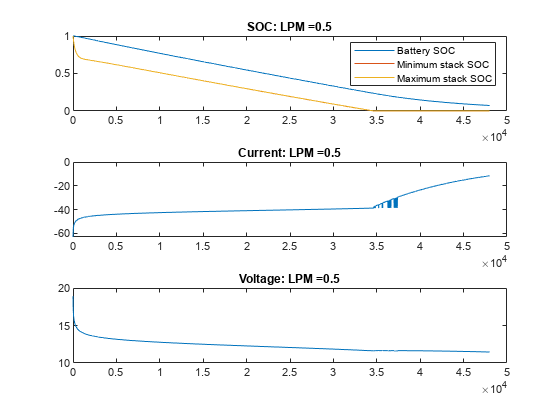
Figure VRFB: LPM =0.5 contains 3 axes objects. Axes object 1 with title SOC: LPM =0.5 contains 3 objects of type line. These objects represent Battery SOC, Minimum stack SOC, Maximum stack SOC. Axes object 2 with title Current: LPM =0.5 contains an object of type line. Axes object 3 with title Voltage: LPM =0.5 contains an object of type line.

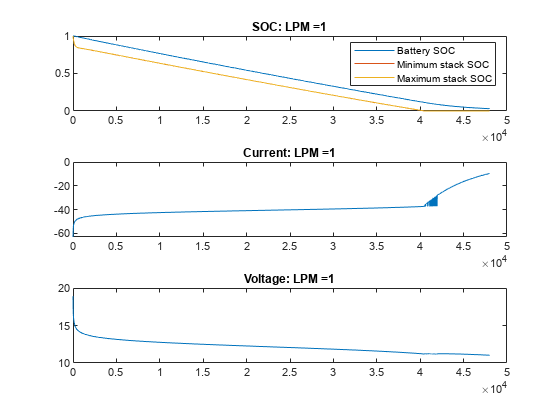
Figure VRFB: LPM =1 contains 3 axes objects. Axes object 1 with title SOC: LPM =1 contains 3 objects of type line. These objects represent Battery SOC, Minimum stack SOC, Maximum stack SOC. Axes object 2 with title Current: LPM =1 contains an object of type line. Axes object 3 with title Voltage: LPM =1 contains an object of type line.

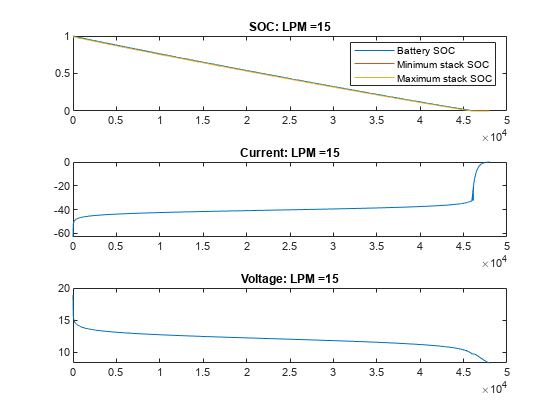
Figure VRFB: LPM =15 contains 3 axes objects. Axes object 1 with title SOC: LPM =15 contains 3 objects of type line. These objects represent Battery SOC, Minimum stack SOC, Maximum stack SOC. Axes object 2 with title Current: LPM =15 contains an object of type line. Axes object 3 with title Voltage: LPM =15 contains an object of type line.

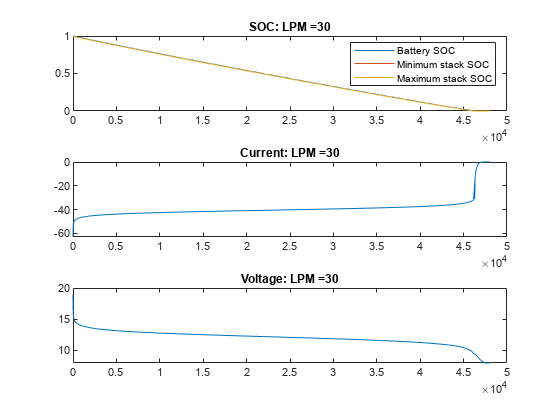
Figure VRFB: LPM =30 contains 3 axes objects. Axes object 1 with title SOC: LPM =30 contains 3 objects of type line. These objects represent Battery SOC, Minimum stack SOC, Maximum stack SOC. Axes object 2 with title Current: LPM =30 contains an object of type line. Axes object 3 with title Voltage: LPM =30 contains an object of type line.

参考资料

[1] Li, Yifeng, Maria Skyllas-Kazacos, and Jie Bao.“A Dynamic Plug Flow Reactor Model for a Vanadium Redox Flow Battery Cell.”Journal of Power Sources 311 (April 2016):57–67. https://doi.org/10.1016/j.jpowsour.2016.02.018

[2] Khaki, Bahman, and Pritam Das.“An Equivalent Circuit Model for Vanadium Redox Batteries via Hybrid Extended Kalman Filter and Particle Filter Methods.”Journal of Energy Storage 39 (July 2021):102587. https://doi.org/10.1016/j.est.2021.102587