求解器
计算仿真状态和输出的求解器
模型配置窗格: 求解器
描述
求解器参数指定在仿真期间和生成的代码中用于计算模型状态的求解器。在求解表示模型所实现的系统的常微分方程组的过程中,求解器还确定仿真的下一个时间步。
当您为引用模型启用引用模型时使用局部求解器参数时,引用模型的求解器参数将指定用作局部求解器的求解器。局部求解器将引用模型作为一组单独的微分方程进行求解。有关详细信息,请参阅Use Local Solvers in Referenced Models。
本软件提供了几种类型的定步长和变步长求解器。
定步长求解器
通常,除了 ode14x 和 ode1be 之外的定步长求解器使用以下公式计算下一时间步:
X(n+1) = X(n) + h dX(n)
其中 X 是状态,h 是步长,dX 是状态导数。dX(n) 是基于方法阶数、通过一次或多次导数运算用特定算法计算得出的。
对于大多数定步长求解器,您可以配置其他参数,包括:
设置
通常,自动求解器选择会为每个模型选择一个合适的求解器。求解器选项取决于几个因素,包括系统动态特性和解的稳定性。有关详细信息,请参阅选择求解器。
对此参数可用的选项取决于您选择的求解器类型。
- 自动(自动求解器选择)
软件将根据模型动态特性选择变步长求解器来计算模型状态。对于大多数模型,软件会选择合适的求解器。
- 离散(无连续状态)
此求解器仅适用于不包含状态或仅包含离散状态的模型。
discrete变步长求解器通过添加取决于模型中状态变化率的步长来计算下一个仿真时间点。- ode45(多曼-普林斯)
当您手动选择求解器时,
ode45是大多数系统的首选。ode45求解器通过使用显式龙格-库塔 (4,5) 公式(也称为多曼-普林斯对)进行数值积分的方式来计算模型状态。- ode23(博加基-尚派恩)
ode23求解器通过使用显式龙格-库塔 (2,3) 公式(也称为博加基-尚派恩对)进行数值积分的方式来计算模型状态。在容差较宽松且刚度适中的情况下,
ode23求解器比 ode45 求解器更高效。- ode113(亚当斯)
ode113求解器使用变阶亚当斯-巴什福特-莫顿 PECE 数值积分方法计算模型状态。ode113求解器使用前面几个时间点处的解来计算当前解。在严格容差条件下,
ode113求解器可能比ode45更高效。- ode15s (stiff/NDF)
ode15s求解器使用变阶数值微分公式 (NDF) 计算模型状态。NDF 公式与后向差分公式(BDF,也称为 Gear 方法)有关,但比后者更高效。ode15s求解器使用前面几个时间点处的解来计算当前解。ode15s求解器在求解刚性问题时更高效。如果ode45求解器失败或效率低下,请尝试使用此求解器。- ode23s (stiff/Mod.Rosenbrock)
ode23s求解器使用修正二阶罗森布罗克公式计算模型状态。ode23s求解器仅使用前一时间步的解来计算当前时间步的解。在容差较宽松的条件下,
ode23s求解器比 ode15s 更高效,并可求解难以使用 ode15s 有效处理的刚性问题。- ode23t (mod. stiff/Trapezoidal)
ode23t求解器使用梯形法则实现来计算模型状态。ode23t求解器仅使用前一时间步的解来计算当前时间步的解。对于刚度适中且需要没有数值阻尼的解的问题,请使用
ode23t求解器来求解。- ode23tb(stiff/TR-BDF2)
ode23tb求解器使用 TR-BDF2 的多步实现来计算模型状态,TR-BD F2 是一个隐式龙格-库塔公式,在第一阶段采用梯形法则,在第二阶段包含一个二阶后向差分公式。从构造上而言,两个阶段均使用相同的迭代矩阵。在容差较宽松的条件下,
ode23tb求解器比 ode15s 更高效,并可求解难以使用 ode15s 求解器有效处理的刚性问题。- odeN (非自适应)
odeN求解器使用非自适应定步长积分公式,采用当前状态值和中间点的逼近状态导数的显函数来计算模型的状态。非自适应
odeN求解器不会调整仿真步长以满足误差约束,但在某些情况下会减小过零检测和离散采样时间的步长。- daessc (适用于 Simscape™ 的 DAE 求解器)
daessc求解器通过求解使用 Simscape 建模的微分代数方程组来计算模型状态。daessc求解器提供的稳健算法专门用于仿真物理方程组建模所产生的微分代数方程。daessc求解器仅适用于 Simscape 产品。
- 自动(自动求解器选择)
软件会根据模型动态特性选择定步长求解器来计算模型状态。对于大多数模型,软件会选择合适的求解器。
- 离散(无连续状态)
此求解器仅适用于不包含状态或仅包含离散状态的模型。
discrete定步长求解器依赖模型中的模块来更新离散状态离散定步长求解器不支持过零检测。
- ode8(多曼-普林斯)
ode8求解器使用八阶多曼-普林斯公式,采用当前状态值和中间点的逼近状态导数的显函数来计算模型的状态。- ode5(多曼-普林斯)
ode5求解器使用五阶多曼-普林斯公式,采用当前状态值和中间点的逼近状态导数的显函数来计算模型的状态。- ode4(龙格-库塔)
ode4求解器使用四阶龙格-库塔 (RK4) 公式,采用当前状态值和状态导数的显函数来计算模型状态。- ode3(博加基-尚派恩)
ode3求解器采用当前状态值和状态导数的显函数计算模型状态。求解器使用博加基-尚派恩公式积分方法来计算状态导数。- ode2(Heun)
ode2求解器使用 Heun 积分方法,采用当前状态值和状态导数的显函数来计算模型状态。- ode1(欧拉)
ode1求解器使用欧拉积分方法,采用当前状态值和状态导数的显函数来计算下一个时间步的模型状态。此求解器比高阶求解器需要更少的计算,但提供的准确性相对较低。- ode14x (extrapolation)
ode14x求解器结合使用牛顿方法和基于当前值的外插方法,采用下一个时间步的状态和状态导数的隐函数来计算模型的状态。在此示例中,X 是状态,dX 是状态导数,h 是步长:X(n+1) - X(n)- h dX(n+1) = 0
此求解器在每步中需要的计算多于显式求解器,但对于给定步长来说更加准确。
- ode1be (后向欧拉)
ode1be求解器是后向欧拉类型的求解器,它使用固定的牛顿迭代次数,计算成本固定。您可以使用ode1be求解器作为ode14x求解器的高效计算定步长替代方案。
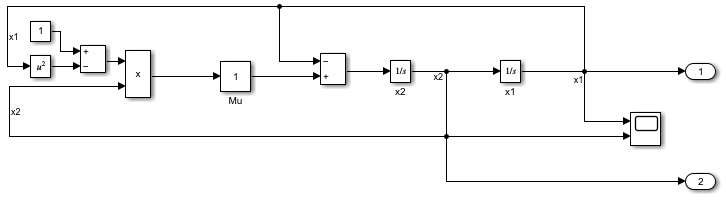
示例
提示
最佳求解器会在可接受的准确度与最短仿真时间之间取得平衡。确定模型的最佳求解器需要进行试验。有关详细信息,请参阅选择求解器。
使用快速重启时,您可以更改仿真的求解器,而不必重新编译模型。 (自 R2021b 起)
本软件对没有状态或只有离散状态的模型使用离散求解器,即使您指定了连续求解器也是如此。
编程用法
参数:SolverName 或 Solver |
| 类型:字符串 | 字符向量 |
变步长求解器值: "VariableStepAuto" | "VariableStepDiscrete" | "ode45" | "ode23" | "ode113" | "ode15s" | "ode23s" | "ode23t" | "ode23tb" | "odeN" | "daessc" |
定步长求解器值: "FixedStepAuto" | "FixedStepDiscrete" | "ode8" | "ode5" | "ode4" | "ode3" | "ode2" | "ode1" | "ode14x" | "ode1be" |
默认值:"VariableStepAuto" |
版本历史记录
在 R2006a 之前推出