对微分代数方程建模
罗伯逊化学反应示例概述
罗伯逊[1] 创建了一个自催化化学反应方程组来测试和比较刚性方程组的数值求解器。方程组中的化学反应、速率常量 (k) 和反应速率 (V) 如下所示:
由于反应速率之间差异较大,因此数值求解器将微分方程视为刚性方程。对于刚性微分方程,有些数值求解器无法收敛得出一个解,除非步长极小。如果步长极小,仿真时间可能长得让人难以接受。在这种情况下,您需要使用设计用于解算刚性方程的数值求解器。
基于 ODE 和 DAE 方程的 Simulink 模型
此示例使用以下三种模型:
ex_hb1ode- 基于常微分方程 (ODE) 的 Simulink® 模型。ex_hb1dae- 基于微分代数方程 (DAE) 的 Simulink 模型。ex_h1bdae_acb- 使用 Algebraic Constraint 模块从 DAE 方程进行 Simulink 建模。
要访问这些文件,请打开实时脚本。
根据 ODE 方程进行 Simulink 建模
常微分方程 (ODE) 组具有以下特征:
所有方程均为常微分方程。
每个方程都是因变量关于自变量(通常是时间)的导数。
方程组中的方程数量等于因变量数量。
使用反应速率,您可以创建一组微分方程,用于描述每个化学物质的变化速率。由于存在三个物质,因此数学模型有三个微分方程。
初始条件:、 和 。
编译模型
创建一个模型,或打开模型 ex_hb1ode。
将三个 Integrator 模块添加到您的模型中。分别标记输入
A'、B'和C'以及输出A、B和C。添加 Sum、Product 和 Gain 模块,以解算每个微分变量。例如,要对信号
C'建模,添加一个 Math Function 模块,并将输入信号连接到
B。将函数参数设置为方波。将 Math Function 模块的输出连接到 Gain 模块。将增益参数设置为
3e7。继续向您的模型中添加剩余的微分方程项。
通过将
AIntegrator 模块的初始条件参数设置为1,为A的初始条件建模。添加 Out 模块以便将信号
A、B和C保存到 MATLAB 变量yout。

对模型进行仿真
创建一个使用 sim 命令对您的模型进行仿真的脚本。该脚本会将仿真结果保存在 MATLAB 变量 yout 中。由于仿真具有较长的时间间隔并且 B 最初的更改速度很快,因此基于对数刻度绘制值有助于直观地比较结果。此外,由于 B 的值相对于 A 和 C 的值来说较小,因此应在绘制值之前将 B 乘以 。
在 MATLAB® 脚本中输入以下语句。如果您已构建自己的模型,请将
ex_hblode替换您模型的名称。sim('ex_hb1ode') yout(:,2) = 1e4*yout(:,2); figure; semilogx(tout,yout); xlabel('Time'); ylabel('Concentration'); title('Robertson Reactions Modeled with ODEs')在 Simulink® 编辑器中,在建模选项卡上,点击模型设置。
- 在“求解器”窗格中,将停止时间设置为
4e5,将求解器设置 ode15s (stiff/NDF)。- 在“数据导入”窗格中,选中时间和输出复选框。
运行脚本。观察是否所有的
A均转换为C。
根据 DAE 方程进行 Simulink 建模
微分代数方程组 (DAE) 具有以下特征:
它同时包含常微分方程和代数方程。代数方程没有任何导数。
只有一些方程是微分方程,它们定义某些因变量的导数。其他因变量使用代数方程定义。
方程组中的方程数量等于因变量数量。
由于守恒定律的原因,例如质量与能量守恒,有些系统包含约束。如果您将初始浓度设置为 、 和 ,由于 ,三个品种的总浓度始终等于 。您可以将 的微分方程替换为以下代数方程,以创建一组微分代数方程 (DAE)。
微分变量 A 和 B 唯一地确定代数变量 C。
初始条件: 和 。
编译模型
对您的模型或模型 ex_hb1ode 进行这些更改,或者打开模型 ex_hb1dae。
删除用于计算
C的 Integrator 模块。添加一个 Sum 模块,并将符号列表参数设置为 +– –。
将信号
A和B连接到 Sum 模块的减号输入。对
A的初始浓度建模,将一个 Constant 模块连接到 Sum 模块的加号输入。将常量值参数设置为1。将 Sum 模块的输出连接到分支线,而该分支线连接到 Product 和 Out 模块。

对模型进行仿真
创建一个使用 sim 命令对您的模型进行仿真的脚本。
在 MATLAB 脚本中输入以下语句。如果您已构建自己的模型,请将
ex_hbldae替换您模型的名称。sim('ex_hb1dae') yout(:,2) = 1e4*yout(:,2); figure; semilogx(tout,yout); xlabel('Time'); ylabel('Concentration'); title('Robertson Reactions Modeled with DAEs')在 Simulink 编辑器中,在建模选项卡上,点击模型设置。
- 在“求解器”窗格中,将停止时间设置为
4e5,将求解器设置 ode15s (stiff/NDF)。- 在“数据导入”窗格中,选中时间和输出复选框。
运行脚本。使用代数方程时的仿真结果与仅使用微分方程时的模型仿真结果相同。

使用 Algebraic Constraint 模块从 DAE 方程进行 Simulink 建模
由于守恒定律的原因,例如质量与能量守恒,有些系统包含约束。如果您将初始浓度设置为 、 和 ,由于 ,三个品种的总浓度始终等于 。
您可以将 的微分方程替换为使用 Algebraic Constraint 模块和 Sum 模块建模的代数方程。Algebraic Constraint 模块将其输入信号 F(z) 限制为零,并输出代数状态 z。换言之,模块输出是令输入为零的值。对模块输入使用以下代数方程。
微分变量 A 和 B 唯一地确定代数变量 C。
初始条件:、 和 。
编译模型
对您的模型或模型 ex_hb1ode 进行这些更改,或者打开模型 ex_hb1dae_acb。
删除用于计算
C的 Integrator 模块。添加一个 Algebraic Constraint 模块。将初始估计值参数设置为
1e-3。添加一个 Sum 模块。将符号列表参数设置为 –+++。
将信号
A和B连接到 Sum 模块的加号输入。使用连接到 Sum 模块的减号输入的 Constant 模块对
A的初始浓度建模。将常量值参数设置为1。将 Algebraic Constraint 模块的输出连接到分支线,而该分支线连接到 Product 和 Out 模块输入。
创建一条从 Algebraic Constraint 模块的输出到 Sum 模块的最终加号输入的分支线。

对模型进行仿真
创建一个使用 sim 命令对您的模型进行仿真的脚本。
在 MATLAB 脚本中输入以下语句。如果您已构建自己的模型,请将
ex_hbl_acb替换您模型的名称。sim('ex_hb1dae_acb') yout(:,2) = 1e4*yout(:,2); figure; semilogx(tout,yout); xlabel('Time'); ylabel('Concentration'); title('Robertson Reactions Modeled with DAEs and Algebraic Constraint Block')在 Simulink 编辑器中,在建模选项卡上,点击模型设置。
- 在“求解器”窗格中,将停止时间设置为
4e5,将求解器设置 ode15s (stiff/NDF)。- 在“数据导入”窗格中,选中时间和输出复选框。
运行脚本。使用 Algebraic Constraint 模块时的仿真结果与仅使用微分方程时的模型仿真结果相同。

使用 Algebraic Constraint 模块在模型中创建一个代数环,如果您将代数环参数设置为警告(在建模选项卡上,点击模型设置,然后选择诊断),则在仿真过程中,以下消息将显示在诊断查看器中。
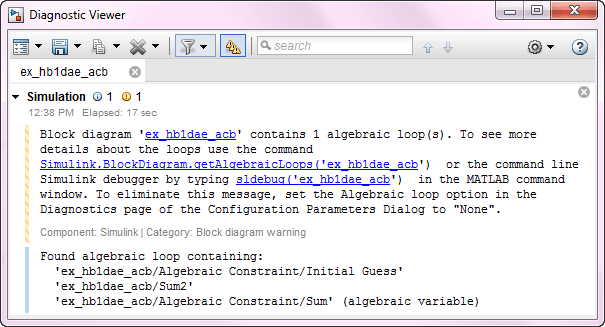
对于此模型,代数环求解器能够对仿真求解,但代数环并不总是具有解,并且它们不支持代码生成。有关 Simulink 模型中的代数环以及如何删除它们的详细信息,请参阅代数环概念。
参考
[1] Robertson, H. H. “The solution of a set of reaction rate equations.” Numerical Analysis: An Introduction (J. Walsh ed.). London, England:Academic Press, 1966, pp. 178–182.