极值搜索控制

极值搜索控制 (ESC) 是一种无模型的实时自适应控制算法，可用于使参数适应未知系统动态特性和从控制参数到目标函数的未知映射。您可以使用极值搜索来解决静态优化问题并优化动态系统的参数。

极值搜索算法使用以下阶段来调整参数值。

调制 - 使用低振幅正弦信号扰动正在优化的参数值。
系统响应 - 正在优化的系统对参数扰动做出反应。此反应会导致目标函数值发生相应变化。
解调 - 将目标函数信号乘以与调制信号频率相同的正弦信号。此阶段包括一个可选的高通滤波器，用于去除目标函数信号中的偏置。
参数更新 - 通过对解调信号进行积分来更新参数值。参数值对应于积分器的状态。该阶段包括一个可选的低通滤波器，用于去除解调信号中的高频噪声。

Simulink^® Control Design™ 软件使用 Extremum Seeking Control 模块实现此算法。有关极值搜索控制的示例，请参阅：

时域

使用 Extremum Seeking Control 模块，您可以实现连续时间控制器和离散时间控制器。两种情况下的 ESC 算法相同。更改控制器的时域会影响调节环路中使用的高通滤波器、低通滤波器和积分器的时域。

要为 Extremum Seeking Control 模块生成硬件可部署代码，请使用离散时间控制器。

下表显示了 Extremum Seeking Control 模块中滤波器和积分器的连续时间传递函数和离散时间传递函数。

控制器元素	连续时间传递函数	离散时间传递函数
高通滤波器	$\frac{s}{s + ω_{h}}$	$\frac{1 - z^{- 1}}{1 - ω_{h} z^{- 1}}$
低通滤波器	$\frac{1}{s + ω_{l}}$	$\frac{1}{1 - ω_{l} z^{- 1}}$
积分器	$\frac{1}{s}$	前向欧拉： $\frac{T_{s}}{z - 1}$ 后向欧拉： $\frac{T_{s} z}{z - 1}$ 梯形： $\frac{T_{s}}{2} \frac{z + 1}{z - 1}$

控制器元素

连续时间传递函数

离散时间传递函数

高通滤波器

$\frac{s}{s + ω_{h}}$

$\frac{1 - z^{- 1}}{1 - ω_{h} z^{- 1}}$

低通滤波器

$\frac{1}{s + ω_{l}}$

$\frac{1}{1 - ω_{l} z^{- 1}}$

积分器

$\frac{1}{s}$

前向欧拉：

$\frac{T_{s}}{z - 1}$

后向欧拉：

$\frac{T_{s} z}{z - 1}$

梯形：

$\frac{T_{s}}{2} \frac{z + 1}{z - 1}$

其中：

ω_l 是低通滤波器截止频率。
ω_h 是高通滤波器截止频率。
T_s 是离散时间控制器学习率的采样时间。

静态优化

为了演示极值搜索，假设有以下静态优化问题。

Extremum seeking control diagram showing the modulation, demodulation, and parameter update stages.

其中：

$\hat{θ}$ 是估计的参数值。
θ 是调制信号。
y = f(θ) 是要最大化的函数输出，即目标函数。
ω 是调制信号和解调信号的强制频率。
b·sin(ωt) 是调制信号。
a·sin(ωt) 是解调信号。
k 是学习率。

最优参数值 θ* 出现在 f(θ) 的最大值处。

要优化多个参数，请对每个参数使用单独的调节环路。

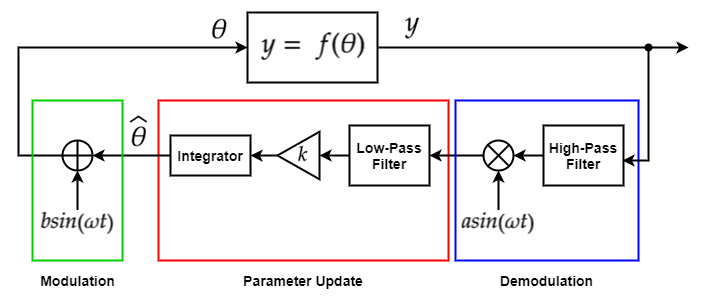
下图演示了对目标函数曲线的上升部分进行极值搜索。调制信号 θ 是当前估计参数和调制信号之和。应用 f(θ) 会产生一个与调制信号相位相同的扰动目标函数。将扰动目标函数乘以解调信号会产生一个正信号。对该信号进行积分会增大 θ 的值，使其更接近目标函数的峰值。

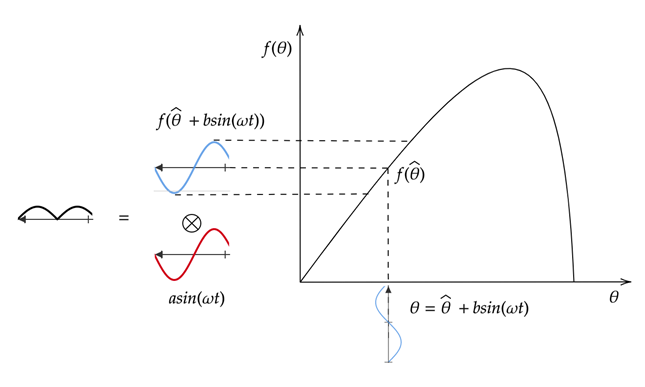
Graph of an objective function with modulation and demodulation demonstrated on an increasing portion of the curve.

下图演示了对目标函数曲线的下降部分进行极值搜索。在本例中，应用 f(θ) 会产生一个与调制信号相位相差 180 度的扰动目标函数。乘以解调信号会产生一个负信号。对该信号进行积分会减小 θ 的值，使其更接近目标函数的峰值。

Graph of an objective function with modulation and demodulation demonstrated on a decreasing portion of the curve

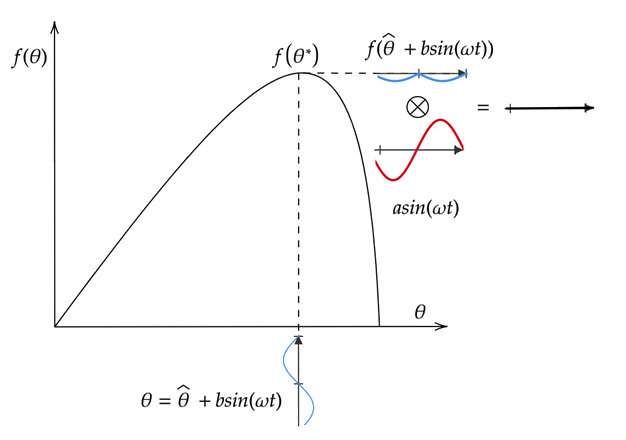
下图演示了对目标函数曲线的平坦部分（即曲线中接近最大值的部分）进行极值搜索。在本例中，应用 f(θ) 会产生一个近零值扰动目标函数。乘以解调信号并对该信号进行积分不会显著改变 θ 的值，该值已经接近其最优值 θ*。

Graph of an objective function with modulation and demodulation demonstrated on a nearly flat portion of the curve

动态系统优化

动态系统的极值搜索优化方式与静态优化类似。但是，在本例中，参数 θ 会影响时间相关动态系统的输出。要最大化的目标函数是根据系统输出计算出来的。下图显示了动态系统的一般调节环路。

Extremum seeking for a time-dependent dynamic system.

其中：

$\dot{x} = f (x, α (x, θ))$ 是动态系统的状态函数。
z = h(x) 是动态系统的输出。
y = g(z) 是从动态系统的输出派生的目标函数。
ϕ₁ 是解调信号的相位。
ϕ₂ 是调制信号的相位。

ESC 设计规范

设计极值搜索控制器时，请考虑以下规范。

确保系统动态特性处于最快时间标度，强制频率处于中等时间标度，滤波器截止频率处于最慢时间标度。
为解调信号指定一个远大于调制信号振幅的振幅 (a ≫ b)。
选择调制信号和解调信号的相位角，使得 cos(ϕ₁ – ϕ₂) > 0。
调节多个参数时，每个调节环路的强制频率必须不同。
尝试设计没有高通滤波器和低通滤波器的系统。如果性能不令人满意，您可以考虑添加其中一种滤波器，或同时添加这两种滤波器。

有关极值搜索控制的详细信息

有关极值搜索控制的详细信息，请播放以下视频。本视频是基于学习的控制系列视频的一部分。

参考

[1] Ariyur, Kartik B., and Miroslav Krstić. Real Time Optimization by Extremum Seeking Control. Hoboken, NJ: Wiley Interscience, 2003.

另请参阅

模块

Extremum Seeking Control