Main Content

Extremum Seeking Control

Compute controller parameters in real time by maximizing objective function

Since R2021a

expand all in page
  • Extremum Seeking Control block

Libraries:
Simulink Control Design / Adaptive Control

Description

The Extremum Seeking Control block tunes controller parameters to maximize an objective function. Extremum seeking controllers are model-free adaptive controllers that are useful for adapting to unknown system dynamics and unknown mappings from control parameters to an objective function. When seeking multiple parameters, the Extremum Seeking Control block uses a separate tuning loop for each parameter.

The Extremum Seeking Control block searches for optimal control parameters by modulating (perturbing) the parameters with sinusoidal signals and demodulating the resulting perturbed objective function.

Extremum seeking control diagram showing the high-pass filter, demodulation, low-pass filter, parameter update, and modulation stages.

To configure the extremum seeking algorithm, set appropriate forcing frequencies, demodulation and modulation signals, learning rates, and parameter initial conditions. When configuring the block, ensure that the system dynamics are on the fastest time scale, the perturbation forcing frequencies are on the medium time scale, and the filter cutoff frequencies are on the slowest time scale.

You can implement both continuous-time and discrete-time extremum seeking controllers. Changing the time-domain of the controller affects the time domain of the high-pass filters, low-pass filters, and integrators used in the tuning loops. To generate hardware-deployable code for the Extremum Seeking Control block, use a discrete-time controller.

For more information, see Extremum Seeking Control.

Examples

Extremum Seeking Control for Reference Model Tracking of Uncertain Systems

Extremum Seeking Control for Reference Model Tracking of Uncertain Systems

Track a reference plant model by adapting feedforward and feedback gains for an uncertain dynamic system.

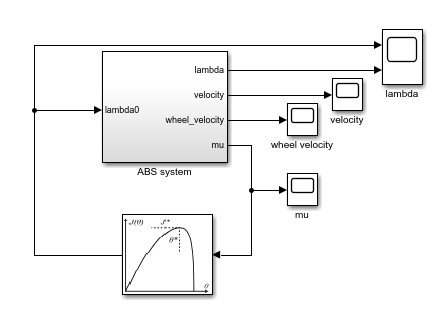
Anti-Lock Braking Using Extremum Seeking Control

Anti-Lock Braking Using Extremum Seeking Control

Design an extremum seeking controller that maximizes the friction coefficient of an ABS system to achieve the shortest stopping distance.

Adaptive Cruise Control Using Extremum Seeking Control

Adaptive Cruise Control Using Extremum Seeking Control

Design an extremum seeking controller to adjust controller gains for an adaptive cruise control system.

Ports

Input

expand all

The objective function from the control system is perturbed as a result of the system response to the perturbed parameters theta. To compute parameter updates, the block filters and demodulates J.

Output

expand all

Apply these perturbed parameters (θ) to your control system. The block uses the resulting perturbation of the objective function J to compute parameter updates.

If Number of parameters is 1, theta outputs a scalar signal. Otherwise, theta outputs a vector signal with length equal to Number of parameters.

Use this output port to obtain the estimated parameter values (θ^) before they are perturbed by the modulation signal.

If Number of parameters is 1, theta_hat outputs a scalar signal. Otherwise, theta_hat outputs a vector signal with length equal to Number of parameters.

Dependencies

To enable this output port, select Output estimated parameters.

Parameters

expand all

Specify the time domain for the high-pass filters, low-pass filters, and integrators.

  • Continuous time — Use continuous-time filters and integrators.

  • Discrete time — Use discrete-time filters and integrators. Specify the sample time using the Sample time parameter, and specify the integration method using the Integration method parameter.

Programmatic Use

Block Parameter: 'timeDomainStatus'
Type: character vector
Values: 'Continuous Time' | 'Discrete Time'
Default: 'Continuous Time'

Specify the sample time for the discrete-time high-pass filters, low-pass filters, and integrators.

When tuning multiple parameters, all tuning loops use the same sample time.

Dependencies

To enable this parameter, set the Time Domain property to Discrete time.

Programmatic Use

Block Parameter: 'SampleTime'
Type: character vector
Values: finite positive scalar
Default: '0.1'

You can select one of the following integration methods for the discrete-time integrators.

  • Forward Euler:

    y(n)=y(n−1)+Ts⋅u(n−1)

  • Backward Euler:

    y(n)=y(n−1)+Ts⋅u(n)

  • Trapezoidal:

    y(n)=y(n−1)+Ts⋅[u(n)+u(n−1)]/2

Here:

  • y is the integrator output

  • u is the input

  • n is the current sample time

  • Ts is the sample time

When tuning multiple parameters, the integrators in all tuning loops use the same integration method.

Dependencies

To enable this parameter, set the Time Domain property to Discrete time.

Programmatic Use

Block Parameter: 'IntegratorMethods'
Type: character vector
Values: 'Forward Euler' | 'Backward Euler' | 'Trapezoidal'
Default: 'Forward Euler'

You can simultaneously tune up to five parameters. The block uses a separate tuning loop for each parameter.

Programmatic Use

Block Parameter: 'paramCount'
Type: character vector
Values: positive integer less than 5
Default: '1'

Initial parameter values, which correspond to the initial conditions of the parameter update integrators.

If Number of parameters is 1, specify Initial condition as a finite scalar.

To specify different initial conditions for multiple parameters, specify Initial condition as a vector of finite values with length equal to Number of parameters. Otherwise, to specify the same initial condition for all parameters, specify Initial condition as a finite scalar.

Programmatic Use

Block Parameter: 'initialVal'
Type: character vector
Values: finite scalar | vector
Default: '0'

Specify the frequency of the modulation and demodulation signals in radians per second. For a given parameter tuning loop, specify a forcing frequency that is lower than the frequencies of important system dynamics and higher than the high-pass and low-pass filter cutoff frequencies.

When tuning a single parameter, specify Forcing frequency as a positive finite scalar.

When tuning a multiple parameters, specify Forcing frequency as a vector of positive finite values with length equal to Number of parameters. Each forcing frequency must be unique, which allows convergence of the extremum-seeking algorithm.

Programmatic Use

Block Parameter: 'omega'
Type: character vector
Values: positive finite scalar | vector
Default: '1'

The learning rate is a gain factor that controls the rate at which the block updates a parameter.

When tuning a single parameter, specify Learning rate as a positive finite scalar.

When tuning a multiple parameters, you can specify a different learning rate for each parameter tuning loop. To do so, specify Learning rate as a vector of positive finite values with length equal to Number of parameters. Otherwise, to specify the same learning rate for all tuning loops, specify Learning rate as a positive finite scalar.

Programmatic Use

Block Parameter: 'gain'
Type: character vector
Values: positive finite scalar | vector
Default: '1'

Specify the amplitude of the signal used to demodulate the objective function. For most applications, specify Demodulation amplitude ≫ Modulation amplitude. The product of these amplitudes, along with the learning rate, controls the convergence speed of the algorithm.

When tuning a single parameter, specify Demodulation amplitude as a positive finite scalar.

When tuning multiple parameters, you can specify a different demodulation amplitude for each parameter tuning loop. To do so, specify Demodulation amplitude as a vector of positive finite values with length equal to Number of parameters. Otherwise, to specify the same amplitude for all tuning loops, specify Demodulation amplitude as a positive finite scalar.

Programmatic Use

Block Parameter: 'demodAmp'
Type: character vector
Default: '1'

Specify the phase ϕ1 of the signal used to demodulate the objective function in radians.

When tuning a single parameter, specify Demodulation phase as a positive finite scalar.

When tuning multiple parameters, you can specify a different demodulation phase for each parameter tuning loop. To do so, specify Demodulation phase as a vector of positive finite values with length equal to Number of parameters. Otherwise, to specify the same phase for all tuning loops, specify Demodulation phase as a positive finite scalar.

The demodulation and modulation phases must satisfy the condition cos(ϕ1–ϕ2) > 0.

Programmatic Use

Block Parameter: 'demodPhase'
Type: character vector
Values: positive finite scalar | vector
Default: '0'

Amplitude of the perturbation signal added to the estimated parameters. For most applications, specify Modulation amplitude ≪ Demodulation amplitude. The product of these amplitudes, along with the learning rate, controls the convergence speed of the algorithm.

When tuning a single parameter, specify Modulation amplitude as a positive finite scalar.

When tuning multiple parameters, you can specify a different modulation amplitude for each parameter tuning loop. To do so, specify Modulation amplitude as a vector of positive finite values with length equal to Number of parameters. Otherwise, to specify the same amplitude for all tuning loops, specify Modulation amplitude as a positive finite scalar.

Programmatic Use

Block Parameter: 'modAmp'
Type: character vector
Values: positive finite scalar | vector
Default: '0.1'

Phase ϕ2 of the perturbation signal added to the estimated parameters, specified in radians. You must select the demodulation phase ϕ1 and modulation phase ϕ2 such that cos(ϕ1–ϕ2) > 0.

When tuning a single parameter, specify Modulation phase as a positive finite scalar.

When tuning multiple parameters, you can specify a different modulation phase for each parameter tuning loop. To do so, specify Modulation phase as a vector of positive finite values with length equal to Number of parameters. Otherwise, to specify the same phase for all tuning loops, specify Modulation phase as a positive finite scalar.

Programmatic Use

Block Parameter: 'modPhase'
Type: character vector
Values: positive finite scalar | vector
Default: '0'

Select this parameter to enable a high-pass filter that removes any signal bias from the objective function signal before the demodulation stage. To specify the filter cutoff frequency, use the HPF frequency parameter.

Programmatic Use

Block Parameter: 'highPassEnable'
Type: character vector
Values: 'off' | 'on'
Default: 'off'

Cutoff frequency ωh for high-pass filtering the objective function signal, specified in radians per second. For a given parameter tuning loop, specify a cutoff frequency such that ωh < ω/(2π), where ω is the corresponding forcing frequency.

When tuning a single parameter, specify HPF frequency as a positive finite scalar.

When tuning multiple parameters, you can specify a different frequency for each parameter tuning loop. To do so, specify HPF frequency as a vector of positive finite values with length equal to Number of parameters. Otherwise, to specify the same frequency for all tuning loops, specify HPF frequency as a positive finite scalar.

Dependencies

To enable this parameter, select the Enable HPF parameter.

Programmatic Use

Block Parameter: 'highPassCutoff'
Type: character vector
Values: positive finite scalar | vector
Default: '1'

Select this parameter to enable a low-pass filter that removes high-frequency components from the demodulated signal before the parameter update stage. To specify the filter cutoff frequency, use the LPF frequency parameter.

Dependencies

To enable this parameter, select the Enable LPF parameter.

Programmatic Use

Block Parameter: 'lowPassEnable'
Type: character vector
Values: 'off' | 'on'
Default: 'off'

Cutoff frequency ωl for low-pass filtering the demodulated signal, specified in radians per second. For a given parameter tuning loop, specify a cutoff frequency such that ωl > ω/(2π), where ω is the corresponding forcing frequency.

When tuning a single parameter, specify LPF frequency as a positive finite scalar.

When tuning multiple parameters, you can specify a different frequency for each parameter tuning loop. To do so, specify LPF frequency as a vector of positive finite values with length equal to Number of parameters. Otherwise, to specify the same frequency for all tuning loops, specify LPF frequency as a positive finite scalar.

Dependencies

To enable this parameter, select the Enable LPF parameter.

Programmatic Use

Block Parameter: 'lowPassCutoff'
Type: character vector
Values: positive finite scalar | vector
Default: '1'

Select this parameter to add the theta_hat output port.

Programmatic Use

Block Parameter: estimatedVarOn
Type: character vector
Values: 'off' | 'on'
Default: 'off'

Extended Capabilities

Version History

Introduced in R2021a

expand all

See Also

Topics