迭代学习控制

迭代学习控制 (ILC) 是一种控制方法，当您想要提高从相同初始工况开始执行重复操作的系统的性能时，该方法非常有用。该方法以前一批量运行的误差轨迹的形式进行频繁测量，来更新后续批量运行的控制信号。ILC 广泛应用于制造业、机器人和化学加工领域的许多实际工业系统，在这些系统中，装配线上的大规模生产涉及重复操作。因此，当您面临重复任务或存在重复扰动并希望运用上一次迭代的知识来改进下一次迭代时，可以使用 ILC。

一般 ILC 更新律具有以下形式（[1] 和 [2]）：

$u_{k + 1} (t) = Q (q) [u_{k} (t) + L (q) e_{k} (t + 1)] .$

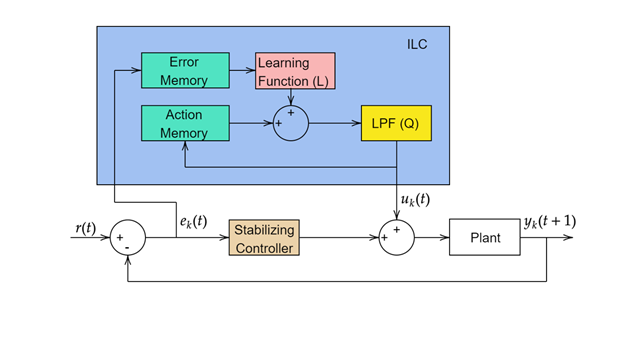
Iterative learning control closed-loop implementation. ILC takes the error signal as an input and provides updated controller actions based on previous iteration.

其中，Q 是用于去除控制震颤的低通滤波器，L 是学习函数。k 表示第 k 次迭代。有多种方法可以设计学习函数。

要在 Simulink^® 中实现 ILC，请使用 Iterative Learning Control 模块。使用此模块，您可以实现无模型 ILC 或基于模型的 ILC。

无模型 ILC

无模型 ILC 不需要系统动态特性的先验知识，并使用比例导数 (PD) 误差反馈来更新控制历史记录。此方法仅适用于 SISO 系统。

无模型 ILC 更新律为：

$u_{k + 1} (t) = Q (q) (u_{k} (t) + γ_{p} e_{k} (t + 1) + γ_{d} (e_{k} (t + 1) - e_{k} (t))) .$

其中，γ_p 和 γ_d 分别是比例增益和导数增益。根据增益的选择，您可以实现 P 型、D 型或 PD 型 ILC。增益 γ_p 和 γ_d 决定了 ILC 在迭代之间的学习表现。如果 ILC 增益太大，可能导致使闭环系统不稳定（稳健性）。如果 ILC 增益太小，可能会导致收敛速度变慢（性能）。通过适当调节 ILC 增益，您可以实现跟踪误差趋于零的标称渐近收敛。

基于模型的 ILC

此方法是 ILC 的更一般形式，适用于以下形式的 SISO 和 MIMO LTI 状态空间系统：

$\begin{array}{l} \begin{matrix} x_{k} (t + 1) = A x_{k} (t) + B u_{k} (t), & x (0) = x_{0}, \end{matrix} \\ y_{k} (t) = C x_{k} (t) . \end{array}$

在此方法中，您根据被控对象输入-输出矩阵 G 设计学习函数 L。基于被控对象动态特性，您可以定义输入-输出关系 Y_k = GU_k + d。其中：

$\begin{array}{l} \begin{matrix} Y_{k} = [\begin{matrix} y (t + 1) \\ y (t + 2) \\ ⋮ \\ y (t + N) \end{matrix}], & U_{k} = [\begin{matrix} u (t) \\ u (t + 2) \\ ⋮ \\ u (t + N - 1) \end{matrix}] \end{matrix} \\ G = [\begin{matrix} C B & 0 & \dots & 0 \\ C A B & C B & \dots & 0 \\ ⋮ & ⋮ & ⋮ & ⋮ \\ C A^{N - 1} B & C A^{N - 2} B & \dots & C B \end{matrix}], \\ d = [\begin{matrix} C A x_{0} & C A^{2} x_{0} & \dots & C A^{N} x_{0} \end{matrix}] . \end{array}$

此外，您可以将误差动态特性表示为：

$e_{k + 1} = (I - G L) e_{k} .$

Iterative Learning Control 模块提供两种类型的基于模型的 ILC：基于梯度的 ILC 和基于逆模型的 ILC。

基于梯度的 ILC 律

基于梯度的 ILC 使用学习函数 L = γG^T 中输入-输出矩阵的转置。因此，ILC 控制律变为：

$u_{k + 1} (t) = Q (q) [u_{k} (t) + γ G^{T} e_{k} (t + 1)]$

误差动态特性为：

$e_{k + 1} = (I - γ G G^{T}) e_{k}$

其中，γ 是 ILC 增益。误差收敛取决于增益的选择。此方法在满足 |1 – γGG^T| < 1 的条件下保证误差收敛。因此，为了实现最快收敛，您可以指定 γ = 1/|G²|。

基于逆模型的 ILC 律

基于逆模型的 ILC 使用学习函数 L = γG^-1 中输入-输出矩阵的逆矩阵。因此，ILC 控制律变为：

$u_{k + 1} (t) = Q (q) [u_{k} (t) + γ G^{- 1} e_{k} (t + 1)] .$

当 G 矩阵不是方阵时，该模块改为使用伪逆矩阵。

误差动态特性为：

$e_{k + 1} = (I - γ G G^{- 1}) e_{k}$

此方法在满足 |1 – γ| < 1 的条件下保证误差收敛。因此，指定小于 2 的正标量以实现收敛。

参考

[1] Bristow, Douglas A., Marina Tharayil, and Andrew G. Alleyne. “A Survey of Iterative Learning Control.” IEEE Control Systems 26, no. 3 (June 2006): 96–114. https://doi.org/10.1109/MCS.2006.1636313.

[2] Gunnarsson, Svante, and Mikael Norrlöf. A Short Introduction to Iterative Learning Control. Linköping University Electronic Press, 1997.

[3] Hätönen, J., T.J. Harte, D.H. Owens, J. Ratcliffe, P. Lewin, and E. Rogers. “Discrete-Time Arimoto ILC-Algorithm Revisited.” IFAC Proceedings Volumes 37, no. 12 (August 2004): 541–46.

[4] Lee, Jay H., Kwang S. Lee, and Won C. Kim. “Model-Based Iterative Learning Control with a Quadratic Criterion for Time-Varying Linear Systems.” Automatica 36, no. 5 (May 1, 2000): 641–57.

[5] Harte, T. J., J. Hätönen, and D. H. Owens *. “Discrete-Time Inverse Model-Based Iterative Learning Control: Stability, Monotonicity and Robustness.” International Journal of Control 78, no. 8 (May 20, 2005): 577–86.

[6] Zhang, Yueqing, Bing Chu, and Zhan Shu. “A Preliminary Study on the Relationship Between Iterative Learning Control and Reinforcement Learning⁎.” IFAC-PapersOnLine, 13th IFAC Workshop on Adaptive and Learning Control Systems ALCOS 2019, 52, no. 29 (January 1, 2019): 314–19. https://doi.org/10.1016/j.ifacol.2019.12.669.

另请参阅

Iterative Learning Control