Measure Three-Phase Electric Circuit Impedance Using Sinestream Signal Generator Block

Examine Model

This example uses a Simulink® model that contains a three-phase circuit as the plant model. The model is preconfigured with a Sinestream Signal Generator block that injects a perturbation signal at the plant input. The model also collects the circuit response data, which you can use for offline frequency response estimation.

Open the model.

mdl = "SineSigGenZPowerGrid.slx";
open_system(mdl)

Electric Circuit

The electric circuit plant model is a three-phase AC network.

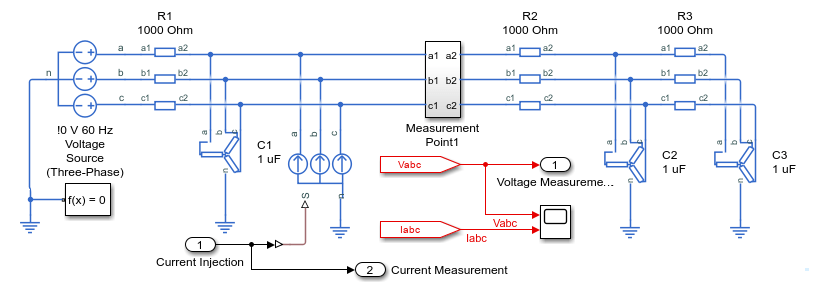
Signal Parameter Settings

The Sinestream Signal Generator block is parameterized to generate a sinestream signal at 20 frequency points between 10 rad/s and 10,000 rad/s, all with amplitudes of 10. In addition, there are three periods of signal for each frequency point. The Signal Length section of the block parameters displays the required experiment length based on the current block parameter settings. To ensure a comprehensive experiment, you must configure the Start-Stop Generator block such that the signal injects for at least that long.

The Advanced Settings section contains parameters that you can use to configure the sinestream signal type and form. You can choose to generate sine signals, cosine signals, or both using the Waveform Type parameter. You can also use the Phase Shift parameter to configure a consistent phase shift in the generated signals.

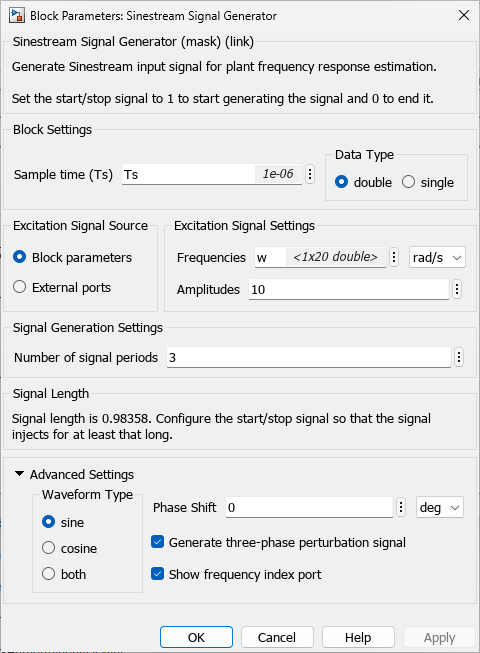
In this example, the Show frequency index port parameter is enabled. This option enables the output port idx w. During simulation, the signal at this port shows the corresponding index of the generated frequency component. A staircase signal helps the post-processing of the logged experiment data. This signal generates a Ready signal similar to the signal output by the Frequency Response Estimator block.

The Generate three-phase perturbation signal parameter allows you to generate balanced three-phase perturbation signals. The generated signal is balanced because the summation of these three-phase signals always equals zero. You can use these signals to analyze three-phase alternating current (AC) electric circuits.

Collect Experiment Data

The Data Logging for 'frestimate' subsystem collects experiment data in the data object SigGenDataLog. The subsystem logs the Ready, Perturbation, PlantInput, and PlantOutput signals in the data object. Inside the Data Logging for 'frestimate' subsystem, the Subtract Nominal Values subsystem removes the nominal values from the logged input and output signals.

Simulate the model. The model injects the generated sinestream perturbation signals into the electric circuit and collects the measurements.

sim(mdl)

The model collects the data in the format compatible for offline frequency response estimation.

SigGenDataLog

SigGenDataLog = struct with fields:
           Ready: [1x1 timeseries]
    Perturbation: [1x1 timeseries]
      PlantInput: [1x1 timeseries]
     PlantOutput: [1x1 timeseries]
            Info: [1x1 struct]

The Ready field is a timeseries signal that contains a logical signal that indicates which time steps contain the data to use for the estimation. For a sinestream signal, this field indicates the settling periods, which are the perturbation periods for the estimation to discard. Perturbation contains the sinestream perturbation applied to the plant. The PlantInput and PlantOutput timeseries signals contain the input and output signals of the plant.

Calculate Analytical Impedance

Based on the circuit model, you can express the impedance as a continuous transfer function. By discretizing the transfer function, you can use it as a reference for the offline frequency response estimation result.

analyticalTF = tf([R^3*C^2 3*R^2*C R],[R^3*C^3 5*R^2*C^2 6*R*C 1])

analyticalTF =
 
        0.001 s^2 + 3 s + 1000
  -----------------------------------
  1e-09 s^3 + 5e-06 s^2 + 0.006 s + 1
 
Continuous-time transfer function.

TFd = c2d(analyticalTF,Ts);
analyticalFRD = frd(TFd,w,"rad/s"); % convert to frd object

Estimate Frequency Response

To perform the frequency response estimation offline, use the collected data with the frestimate function.

Use the SigGenDataLog structure and the specified frequencies as inputs to the frestimate function. frestimate processes SigGenDataLog to obtain a frequency response data model that contains the estimated responses at the specified frequencies.

sys_estim = frestimate(SigGenDataLog,w,"rad/s");
size(sys_estim)

FRD model with 1 outputs, 1 inputs, and 20 frequency points.

Examine Estimated Frequency Response

Compare the frequency response estimation result with the derived analytical transfer function.

ZdataOffline = reshape(sys_estim.ResponseData,[1,Nf]);
ZdataAnalytical = reshape(analyticalFRD.ResponseData,[1,Nf]);
figure;
subplot(2,1,1);
semilogx(w/(2*pi),abs(ZdataOffline),'b*'); 
hold on
semilogx(w/(2*pi),abs(ZdataAnalytical),'ro');
ylabel('Amplitude [Ohm]');
legend('Offline FRE','Analytical');
grid on;
subplot(2,1,2);
semilogx(w/(2*pi),angle(ZdataOffline)*180/pi,'b*');
hold on
semilogx(w/(2*pi),angle(ZdataAnalytical)*180/pi, 'ro');
xlabel('Frequency [Hz]');
ylabel('theta [deg]');
grid on;

The impedance measurement matches the analytical results from the derived transfer function.

You can also use the Sinestream Signal Generator block to conduct impedance measurement in a single-phase circuit. Additionally, you can also conduct multiple frequency response estimation experiments over various operating conditions.