Model Reference Adaptive Control of Aircraft Undergoing Wing Rock
This example shows how to control roll and roll rate of a delta wing aircraft undergoing wing rock. For this example, the system model is unknown. Therefore, you use model reference adaptive control (MRAC) to make the controlled system match an ideal reference model. The aircraft is modeled in Simulink® and the MRAC controller is implemented using the Model Reference Adaptive Control block provided by Simulink Control Design™ software.
Wing-Rock Control System
Wing rock is a phenomenon observed in delta wing aircraft flying at low speeds and high angles of attack. The aircraft experiences undesired roll oscillations that make the aircraft more difficult for the pilot to control. The goal of the MRAC controller is to cancel the undesired roll oscillation. You can then design a baseline controller to achieve a desired reference behavior.
The following equations define the dynamics for the wing-rock model.
Here:
is the system state vector, where is the roll angle and is the roll rate.
is the aileron angle control input for the aircraft.
is the control effective matrix for which you know at least the sign.
is the wing-rock disturbance.
are unknown ideal weights.
For this uncertain nonlinear system, your goal is to design a controller that enables the system to track the following second-order reference model.
Here:
is the reference model state vector.
is the roll reference signal provided by the pilot.
Nominal and Reference Models
Specify the following simplified second-order nominal model for the roll dynamics.
A = [0 1; 0 0]; % Second integrator model B = [0;1]; % Nominal control effective matrix
Define the reference model as the stable second-order system defined previously. The controller adapts its uncertainty model to achieve the same second-order behavior as this model.
Am = [0 1; -4 -2]; % Second integrator model Bm = [0;4]; % Nominal control effective matrix
Specify the initial conditions for the nominal and reference models.
theta_0 = 0; % Initial roll angle (rad) p0 = 0; % Initial roll rate (rad/s) xm = [0;0]; % Initial condition of the reference plant model
Model Reference Adaptive Control Structure
The goal of the MRAC controller is to achieve asymptotic convergence of the tracking error .
The MRAC controller has the following structure.
Here:
contains feedback control gains.
contains feedforward control gains.
is an adaptive control term that cancels the model uncertainty.
The Model Reference Adaptive Control block adjusts the adaptive control term to achieve the desired reference model tracking. Optionally, you can also adapt the feedback and feedforward control gains. Though, for this example, the control gains are static.
The static feedback and feedforward control gains for the wing-rock system are computed to satisfy the following model-matching condition.
Specify the computed controller gains.
Kx = [-4 -2]; % Feedback gain Kr = 4; % Feedforward gain
Uncertainty Estimation Parameters
The MRAC controller estimates the model uncertainty online and generates an adaptive control action that cancels the uncertainty to recover the nominal system for the baseline controller. The adaptive control term models the system uncertainty using the following model.
Here:
contains the network weights that are adjusted by the controller.
is the uncertainty model feature vector.
Using the Model Reference Adaptive Control block, you can select one of the following feature vector definitions.
System states, where — This approach is the simplest option, which can be a good starting point if you do not know the complexity of the system uncertainty. If you find that using the states as features does not adequately represent the nonlinear uncertainty, select one of the other approaches.
Radial basis functions (RBFs) with Gaussian kernels, where . You can configure the kernels by defining the feature centers and bandwidths .
Single hidden layer (SHL) neural network with a specified number of neurons in the hidden layer.
Custom features provided by an optional input port.
For this example, you configure the controller to use all four methods and compare the results.
Define the model estimation learning rate gamma_w and tracking error weight Q. These parameters are used for all three controller configurations.
gamma_w = 100; % Learning rate Q = 1; % Tracking error weight
Specify the parameters for the radial basis function kernels. Generally, you configure the RBF centers to span the possible state space of the system and the bandwidth to provide sufficient overlap between the kernels.
N = 10; % Number of RBF kernels cen_max = 2; % Upper limit for kernel centers cen_min = -2; % Lower limit for kernel centers bandwidth = 25; % Kernel bandwidth
Simulate Controller Using State Feature Vector
Open a Simulink model of the wing-rock control system configured to use the system states as the uncertainty model feature vector.
mdl = "wingrockStates";
open_system(mdl)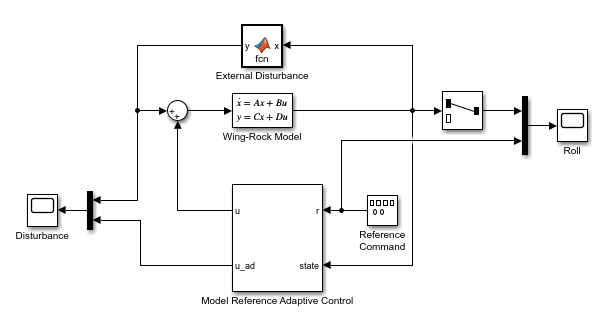
In this model:
The Wing-Rock Model block implements the nominal model of the roll dynamics.
The External Disturbance block generates a wing-rock disturbance of the roll dynamics.
The Reference Command block generates the pilot reference signal.
The Model Reference Adaptive Control block outputs the control action and estimate of the wing-rock disturbance.
Set the simulation duration and simulate the model.
Tf = 40; % Simulation duration (s)
sim(mdl);Compare the resulting aircraft roll to the reference command.
open_system(mdl + "/Roll")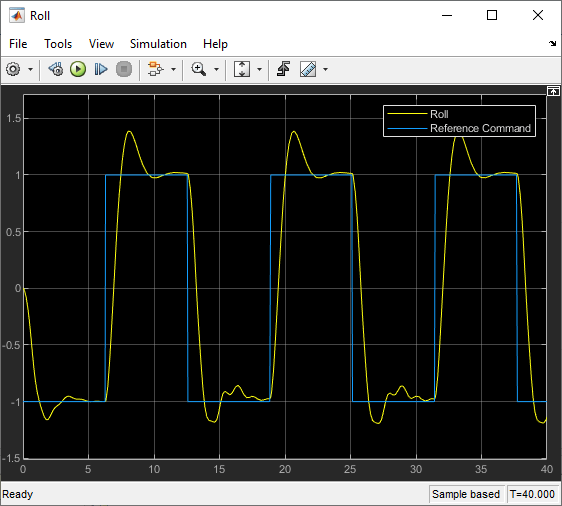
The controller does not achieve a smooth second-order transient response.
Compare the disturbance model estimated by the MRAC controller with the true disturbance signal.
open_system(mdl + "/Disturbance")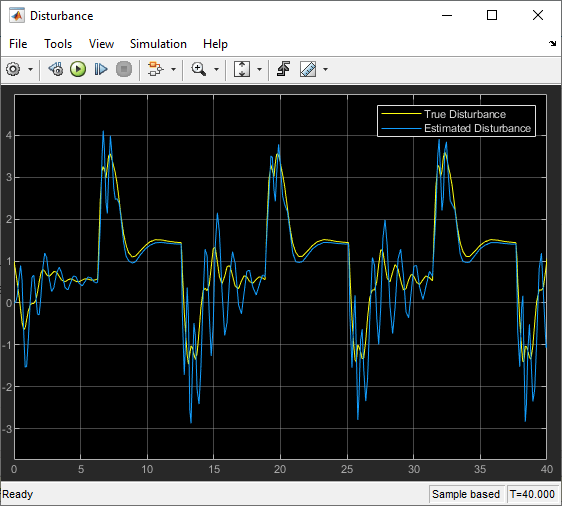
When using the states as the disturbance model features, the linear disturbance model estimated by the controller does not accurately represent the true nonlinear disturbance.
Simulate Controller Using RBF Feature Vector
Open a Simulink model of the wing-rock control system configured to use the nonlinear RBFs as the uncertainty model feature vector. This model is identical to the previous model except that the controller parameters have been updated.
mdl = "wingrockRBF";
open_system(mdl)Simulate the model.
sim(mdl);
View the resulting controller performance.
open_system(mdl + "/Roll")
The controller achieves a smoother second-order response for changes in the reference command.
Compare the disturbance estimated using the radial basis functions to the true disturbance.
open_system(mdl + "/Disturbance")
The nonlinear feature vector allows the controller to more accurately estimate the true nonlinear disturbance.
Simulate Controller Using SHL Neural Network Feature Vector
Open a Simulink model of the wing-rock control system configured to use the SHL neural network output as the uncertainty model feature vector. This model is identical to the previous model except that the controller parameters have been updated.
mdl = "wingrockSHL";
open_system(mdl)Simulate the model.
sim(mdl);
View the resulting controller performance.
open_system(mdl + "/Roll")
The controller achieves a smooth second-order response for changes in the reference command.
Compare the disturbance estimated using the SHL neural network to the true disturbance.
open_system(mdl + "/Disturbance")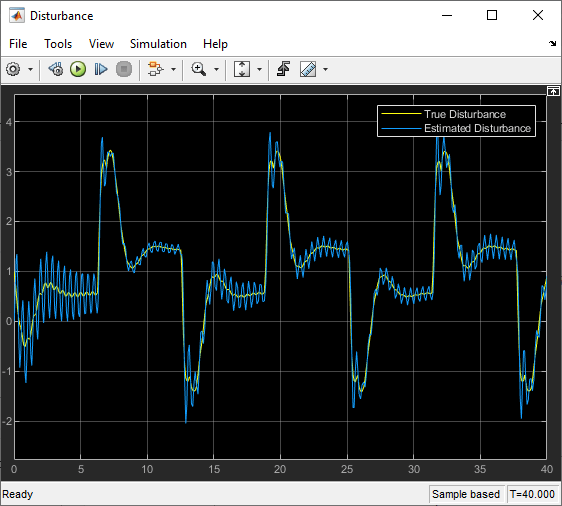
The nonlinear feature vector computed by the neural network approximator is closer to the true disturbance than the RBF feature vector. Configuring the neural network parameters is also simpler.
Simulate Controller Using Custom Feature Vector
Open a Simulink model of the wing-rock control system configured to use an externally generated custom uncertainty model feature vector. You can use this option when you know the structure of the disturbance and uncertainty model. For this example, the feature vector generated by the Features block matches the feature vector used in the External Disturbance block.
mdl = "wingrockCustom";
open_system(mdl)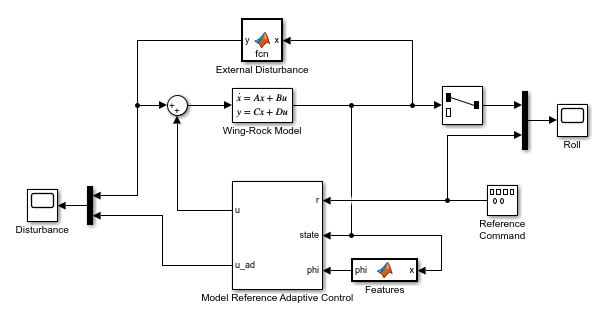
Simulate the model.
sim(mdl);
View the resulting controller performance.
open_system(mdl + "/Roll")
The controller achieves a smoother second-order response for changes in the reference command.
Compare the disturbance estimated using the custom feature vector to the true disturbance.
open_system(mdl + "/Disturbance")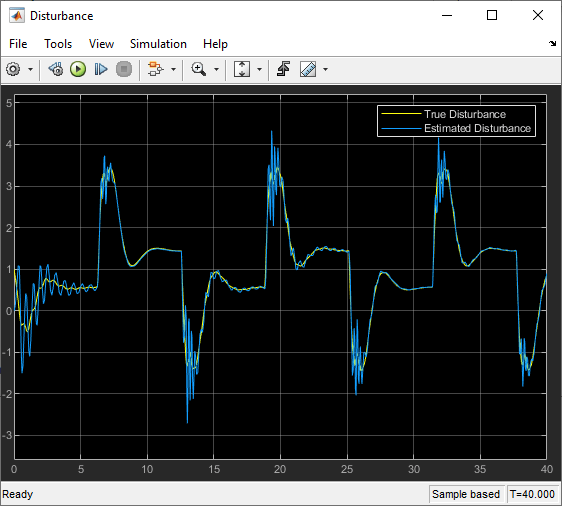
As expected, using a custom feature vector based on prior knowledge of the disturbance behavior produces a more accurate model of the true disturbance.