Controller Poles Goal

Purpose

Constrain the dynamics of a specified tunable block in the tuned control system, when using Control System Tuner.

Description

Controller Poles Goal constrains the dynamics of a tunable block in your control system model. Controller Poles Goal can impose a stability constraint on the specified block. You can also specify a finite minimum decay rate, a minimum damping rate, or a maximum natural frequency for the poles of the block. These constraints allow you to eliminate fast dynamics and control ringing in the response of the tunable block.

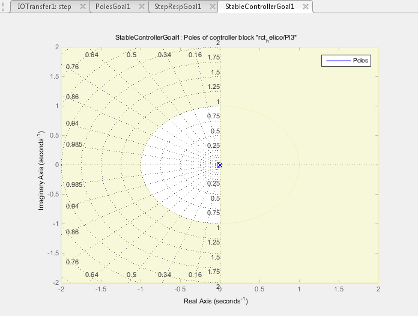
In Control System Tuner, the shaded area on the plot represents the region in the frequency domain where the pole location constraints are not met. The constraint applies to all poles in the block except fixed integrators, such as the I term of a PID controller.

To constrain dynamics or ensure stability of an entire control system or a feedback loop in the control system, use Poles Goal.

Creation

In the Tuning tab of Control System Tuner, select New Goal > Constraint on controller dynamics to create a Controller Poles Goal.

Command-Line Equivalent

When tuning control systems at the command line, use TuningGoal.ControllerPoles to specify a controller poles goal.

Constrain Dynamics of Tuned Block

From the drop-down menu, select the tuned block in your control system to which to apply the Controller Poles Goal.

If the block you want to constrain is not in the list, add it to the Tuned Blocks list. In Control System Tuner, in the Tuning tab, click Select Blocks. For more information about adding tuned blocks, see Specify Blocks to Tune in Control System Tuner.

Keep Poles Inside the Following Region

Use this section of the dialog box to specify the limits on pole locations.

Minimum decay rate
Enter the desired minimum decay rate for the poles of the tunable block. Poles of the block are constrained to satisfy Re(s) < -MinDecay for continuous-time blocks, or log(|z|) < -MinDecay*Ts for discrete-time blocks with sample time Ts.
Specify a nonnegative value to ensure that the block is stable. If you specify a negative value, the tuned block can include unstable poles.
Minimum damping
Enter the desired minimum damping ratio of poles of the tunable block, as a value between 0 and 1. Poles of the block that depend on the tunable parameters are constrained to satisfy Re(s) < -MinDamping*|s|. In discrete time, the damping ratio is computed using s=log(z)/Ts.
Maximum natural frequency
Enter the target maximum natural frequency of poles of the tunable block, in the units of the control system model you are tuning. Poles of the block are constrained to satisfy |s| < MaxFrequency for continuous-time blocks, or |log(z)| < MaxFrequency*Ts for discrete-time blocks with sample time Ts. This constraint prevents fast dynamics in the tunable block.

Algorithms

When you tune a control system, the software converts each tuning goal into a normalized scalar value f(x). Here, x is the vector of free (tunable) parameters in the control system. The software then adjusts the parameter values to minimize f(x) or to drive f(x) below 1 if the tuning goal is a hard constraint.

For Controller Poles Goal, f(x) reflects the relative satisfaction or violation of the goal. For example, if your Controller Poles Goal constrains the pole of a tuned block to a minimum damping of ζ = 0.5, then:

f(x) = 1 means the damping of the pole is ζ = 0.5 exactly.
f(x) = 1.1 means the damping is ζ = 0.5/1.1 = 0.45, roughly 10% less than the target.
f(x) = 0.9 means the damping is ζ = 0.5/0.9 = 0.55, roughly 10% better than the target.