Low-Pass Filter (Discrete or Continuous)
离散时间或连续时间低通滤波器
库:
Simscape /
Electrical /
Control /
General Control
描述
Low-Pass Filter (Discrete or Continuous) 模块实现符合 IEEE 421.5-2016[1] 标准的低通滤波器。在该标准中，滤波器称为简单时间常数。
您可以使用采样时间参数在积分器的连续实现和离散实现之间切换。
方程
要配置连续时间滤波器，请将采样时间属性设置为 0。这种表示形式等效于以下连续传递函数：
其中：
K 是滤波器增益。
T 是滤波器时间常数。
根据前面的传递函数，滤波器定义方程为：
其中：
u 是滤波器输入。
x 是滤波器状态。
y 是滤波器输出。
t 是仿真时间。
u0 是模块的初始输入。
要配置离散时间滤波器，请将采样时间属性设置为正的非零值，或设置为 -1 以从上游模块继承采样时间。离散表示形式等效于以下传递函数：
其中：
K 是滤波器增益。
T 是滤波器时间常数。
Ts 是滤波器采样时间。
根据离散传递函数，滤波器方程使用前向欧拉法定义：
其中：
u 是滤波器输入。
x 是滤波器状态。
y 是滤波器输出。
n 是仿真时间步。
u0 是模块的初始输入。
初始条件
要指定此模块的初始条件，请将初始化设置为：
从模块输入继承 - 模块将状态和输出初始条件设置为初始输入。
指定为参数 - 模块将状态初始条件设置为初始状态的值。
积分限幅
设置饱和上限和饱和下限参数以使用抗积分饱和方法。
抗积分饱和方法将积分器状态限制在饱和下限 A 和饱和上限 B 之间：
由于状态受到限制，因此当积分饱和时，输出可以在输入符号反转时立即做出响应。下面的模块图形象地说明了抗积分饱和方法在滤波器中的实现方式。
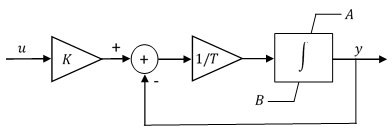
此模块不提供积分饱和方法。要使用积分饱和方法，请将饱和上限参数设置为 inf，将饱和下限参数设置为 -inf，并在输出端添加一个 saturation 模块。
旁路滤波器动态特性
将时间常数设置为小于或等于采样时间的值可忽略滤波器的动态特性。旁路动态特性时，模块将经过增益缩放的输入直接馈送到输出：
在连续时间情况下，采样时间和时间常数都必须为零。
示例
电动发动机测功机
此示例展示了如何对电动汽车测功机测试进行建模。测试环境包含一台异步电机 (ASM) 和一台内置式永磁同步电机 (IPMSM)，它们通过机械轴背靠背连接。这两台电机均由高压电池通过受控三相转换器供电。由功率为 164 kW 的 ASM 产生负载转矩。功率为 35 kW 的 IPMSM 是在测电机。Control Machine Under Test (IPMSM) 子系统控制 IPMSM 的转矩。该控制器包括基于 PI 的多速率控制结构。开环转矩控制的速率低于闭环电流控制的速率。控制器的任务调度以 Stateflow® 状态机的形式实现。Control Load Machine (ASM) 子系统使用单速率来控制 ASM 的转速。Visualization 子系统包含示波器，可用于查看仿真结果。
带传感器控制的三相异步驱动
此示例展示了如何使用带传感器转子磁场定向控制来控制和分析异步电机 (ASM) 的运行。该模型展示了主电路，以及包含控制、测量和示波器的三个附加子系统。Controls 子系统包含两个控制器：一个用于电网侧转换器 (AC/DC)，另一个用于电机侧转换器 (DC/AC)。Scopes 子系统包含两个示波器：一个用于电网侧转换器，另一个用于 ASM。执行该模型时，频谱分析仪会打开并显示 A 相电源电流的频率数据。
无传感器控制的三相异步驱动
此示例展示了如何使用无传感器转子磁场定向控制来控制和分析异步电机 (ASM) 的运行。该模型展示了主电路，以及包含控制、测量和示波器的三个附加子系统。Controls 子系统包含两个控制器：一个用于电网侧转换器 (AC/DC)，另一个用于电机侧转换器 (DC/AC)。Scopes 子系统包含两个示波器：一个用于电网侧转换器，另一个用于 ASM。执行该模型时，频谱分析仪会打开并显示 A 相电源电流的频率数据。
端口
输入
输出
参数
参考
[1] IEEE Recommended Practice for Excitation System Models for Power System Stability Studies. IEEE Std 421.5-2016. Piscataway, NJ: IEEE-SA, 2016.
扩展功能
版本历史记录
在 R2017b 中推出
