Main Content

SM AC6C

Discrete-time or continuous-time synchronous machine AC6C excitation system including an automatic voltage regulator and an exciter

Since R2020a

expand all in page
  • SM AC6C block

Libraries:
Simscape / Electrical / Control / SM Control

Description

The SM AC6C block implements a synchronous machine type AC6C excitation system model in conformance with IEEE 421.5-2016[1].

Use this block to model the control and regulation of the field voltage of a synchronous machine that operates as a generator using an AC rotating exciter.

You can switch between continuous and discrete implementations of the block by using the Sample time (-1 for inherited) parameter. To configure the integrator for continuous time, set the Sample time (-1 for inherited) property to 0. To configure the integrator for discrete time, set the Sample time (-1 for inherited) property to a positive, nonzero value, or to -1 to inherit the sample time from an upstream block.

The SM AC6C block is made up of four major components:

  • The Current Compensator modifies the measured terminal voltage as a function of terminal current.

  • The Voltage Measurement Transducer simulates the dynamics of a terminal voltage transducer using a low-pass filter.

  • The Excitation Control Elements component compares the voltage transducer output with a terminal voltage reference to produce a voltage error. This voltage error is then passed through a voltage regulator to produce the exciter field voltage.

  • The AC Rotating Exciter models the AC rotating exciter, which produces a field voltage that is applied to the controlled synchronous machine. The block also feeds the exciter field current (which is given the standard symbol VFE) back to the excitation system.

This diagram shows the overall structure of the AC6C excitation system model:

In the diagram:

  • VT and IT are the measured terminal voltage and current of the synchronous machine.

  • VC1 is the current-compensated terminal voltage.

  • VC is the filtered, current-compensated terminal voltage.

  • VREF is the reference terminal voltage.

  • VS is the power system stabilizer voltage.

  • EFE and VFE are the exciter field voltage and current, respectively.

  • EFD and IFD are the field voltage and current, respectively.

The following sections describe each of the major parts of the block in detail.

Current Compensator and Voltage Measurement Transducer

The current compensator is modeled as:

VC1=VT+ITRC2+XC2,

where:

  • RC is the load compensation resistance.

  • XC is the load compensation reactance.

The voltage measurement transducer is implemented as a Low-Pass Filter block with time constant TR. Refer to the documentation for this block for the discrete and continuous implementations.

Excitation Control Elements

This diagram illustrates the overall structure of the excitation control elements:

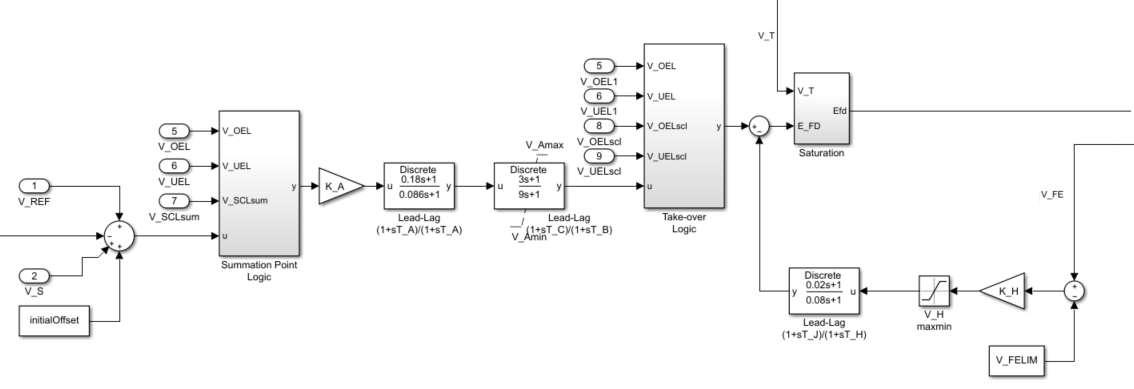
In the diagram:

  • The Summation Point Logic subsystem models the summation point input location for the overexcitation limiter (OEL), underexcitation limiter (UEL), and stator current limiter (SCL) voltages. For more information about using limiters with this block, see Field Current Limiters.

  • A network of two Lead-Lag blocks models the dynamics of the voltage regulator. KA is the regulator gain and TA is the major time constant of the regulator. The second block models additional dynamics associated with the voltage regulator. Here, TC is the lead time constant and TB is the lag time constant. Refer to the documentation for the Lead-Lag block for the discrete and continuous implementations.

  • The Take-over Logic subsystem models the take-over point input location for the OEL, UEL, and SCL voltages. For more information about using limiters with this block, see Field Current Limiters.

  • Another Lead-Lag block models the rate feedback path for the stabilization of the excitation system. Here, KH is the gain of this system and TJ and TH are the lead and lag time constants, respectively.

  • The Saturation subsystem models the minimum, VT*EFEmin, and the maximum, VT*EFEmax, saturation limits for the output exciter field voltage EFE.

  • The initialOffset Constant block ensures the simulation can start from a steady state. The SM AC6C block calculates this value by using saturation and exciter parameters, including the initial field voltage and the regulator output gain.

Field Current Limiters

You can use various field current limiters to modify the output of the voltage regulator under unsafe operating conditions:

  • Use an overexcitation limiter to prevent overheating of the field winding due to excessive field current demand.

  • Use an underexcitation limiter to boost field excitation when it is too low, which risks desynchronization.

  • Use a stator current limiter to prevent overheating of the stator windings due to excessive current.

Attach the output of any of these limiters at one of these points:

  • The summation point as part of the automatic voltage regulator (AVR) feedback loop

  • The take-over point to override the usual behavior of the AVR

If you are using the stator current limiter at the summation point, use the single input VSCLsum. If you are using the stator current limiter at the take-over point, use both the overexcitation input, VOELscl, and the underexcitation input, VUELscl.

AC Rotating Exciter

This diagram shows the structure of the AC rotating exciter:

In the diagram:

  • The exciter field current VFE is the sum of three signals:

    • The nonlinear function Vx models the saturation of the exciter output voltage.

    • The proportional term KE models the linear relationship between the exciter output voltage and the exciter field current.

    • The subsystem models the demagnetizing effect of the load current on the exciter output voltage using the demagnetization constant KD in the feedback loop.

  • The Integrator with variable limits subsystem integrates the difference between EFE and VFE to generate the exciter alternator output voltage VE. TE is the time constant for this process.

  • The nonlinear function FEX models the exciter output voltage drop from the rectifier regulation. This function depends on the constant KC, which itself is a function of commutating reactance.

  • The parameters VEmin and VFEmax model the lower and upper limits of the rotating exciter.

Ports

Input

expand all

Voltage regulator reference set point, in per-unit representation, specified as a scalar.

Data Types: single | double

Input from the power system stabilizer, in per-unit representation, specified as a scalar.

Data Types: single | double

Terminal voltage magnitude in per-unit representation, specified as a scalar.

Data Types: single | double

Terminal current magnitude in per-unit representation, specified as a scalar.

Data Types: single | double

Input from the overexcitation limiter, in per-unit representation, specified as a scalar.

Dependencies

  • To ignore the input from the overexcitation limiter, set Alternate OEL input locations (V_OEL) to Unused.

  • To use the input from the overexcitation limiter at the summation point, set Alternate OEL input locations (V_OEL) to Summation point.

  • To use the input from the overexcitation limiter at the take-over point, set Alternate OEL input locations (V_OEL) to Take-over.

Data Types: single | double

Input from the underexcitation limiter, in per-unit representation, specified as a scalar.

Dependencies

  • To ignore the input from the underexcitation limiter, set Alternate UEL input locations (V_UEL) to Unused.

  • To use the input from the underexcitation limiter at the summation point, set Alternate UEL input locations (V_UEL) to Summation point.

  • To use the input from the underexcitation limiter at the take-over point, set Alternate UEL input locations (V_UEL) to Take-over.

Data Types: single | double

Input from the stator current limiter when using the summation point, in per-unit representation, specified as a scalar.

Dependencies

  • To ignore the input from the stator current limiter, set Alternate SCL input locations (V_SCL) to Unused.

  • To use the input from the stator current limiter at the summation point, set Alternate SCL input locations (V_SCL) to Summation point.

Data Types: single | double

Input from the stator current limiter to prevent field overexcitation when using the take-over point, in per-unit representation, specified as a scalar.

Dependencies

  • To ignore the input from the stator current limiter, set Alternate SCL input locations (V_SCL) to Unused.

  • To use the input from the stator current limiter at the take-over point, set Alternate SCL input locations (V_SCL) to Take-over.

Data Types: single | double

Input from the stator current limiter to prevent field underexcitation when using the take-over point, in per-unit representation, specified as a scalar.

Dependencies

  • To ignore the input from the stator current limiter, set Alternate SCL input locations (V_SCL) to Unused.

  • To use the input from the stator current limiter at the take-over point, set Alternate SCL input locations (V_SCL) to Take-over.

Data Types: single | double

Measured per-unit field current of the synchronous machine, specified as a scalar.

Data Types: single | double

Output

expand all

Per-unit field voltage to apply to the field circuit of the synchronous machine, returned as a scalar.

Data Types: single | double

Parameters

expand all

General

Initial per-unit voltage to apply to the field circuit of the synchronous machine.

Time between consecutive block executions. During execution, the block produces outputs and, if appropriate, updates its internal state. For more information, see What Is Sample Time? and Specify Sample Time.

For inherited discrete-time operation, set this parameter to -1. For discrete-time operation, set this parameter to a positive integer. For continuous-time operation, set this parameter to 0.

If this block is in a masked subsystem or a variant subsystem that supports switching between continuous operation and discrete operation, promote this parameter to ensure correct switching between the continuous and discrete implementations of the block. For more information, see Promote Block Parameters on a Mask.

Pre-Control

Resistance used in the current compensation system. Set this parameter and Reactance component of load compensation, X_C (pu) to 0 to disable current compensation.

Reactance used in the current compensation system. Set this parameter and Resistive component of load compensation, R_C (pu) to 0 to disable current compensation.

Equivalent time constant for the voltage transducer filtering.

Control

Gain associated with the voltage regulator.

Major time constant of the voltage regulator.

Equivalent lag time constant in the voltage regulator. Set this parameter to 0 when the additional lag dynamics are negligible.

Equivalent lead time constant in the voltage regulator. Set this parameter to 0 when the additional lead dynamics are negligible.

Equivalent lead time constant in the voltage regulator. Set this parameter to 0 when the additional lead dynamics are negligible.

Per-unit gain of the field current limiter of the excitation system.

Maximum per-unit output of the field current limiter of the excitation system.

Per-unit reference of the field current limiter of the excitation system.

Equivalent lag time constant in the exciter field current limiter. Set this parameter to 0 when the additional lag dynamics are negligible.

Equivalent lead time constant in the exciter field current limiter. Set this parameter to 0 when the additional lag dynamics are negligible.

Maximum per-unit output voltage of the regulator.

Minimum per-unit output voltage of the regulator.

Maximum per-unit field voltage to be applied to exciter.

Minimum per-unit field voltage to be applied to exciter.

Location of the overexcitation limiter.

Location of the underexcitation limiter.

Location of the stator current limiter input:

  • If you select Summation point, use the V_SCLsum input port.

  • If you select Take-over, use the V_OELscl and V_UELscl input ports.

Exciter

Proportional constant for the exciter field.

Time constant for the exciter field.

Rectifier loading factor proportional to the commutating reactance.

Demagnetization factor related to the exciter alternator reactances.

Exciter output voltage for the first saturation factor.

Saturation factor for the first exciter.

Exciter output voltage for the second saturation factor.

Saturation factor for the second exciter.

Maximum per-unit field current limit reference.

Minimum per-unit exciter voltage output.

References

[1] IEEE Recommended Practice for Excitation System Models for Power System Stability Studies. IEEE Std 421.5-2016. Piscataway, NJ: IEEE-SA, 2016.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2020a

See Also

Blocks