Variable-Frequency Second-Order Filter

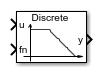
Discrete-time or continuous-time variable-frequency second-order filter

Libraries:
Simscape / Electrical / Control / General Control

Description

The Variable-Frequency Second-Order Filter block implements four different types of second-order filters, each with external frequency input.. Filters are useful for attenuating noise in measurement signals.

The block provides these filter types:

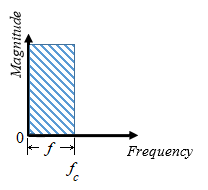
Low pass — Allows signals, $f$ , only in the range of frequencies below the cutoff frequency, $f_{c}$ , to pass.
High pass — Allows signals, $f$ , only in the range of frequencies above the cutoff frequency, $f_{c}$ , to pass.
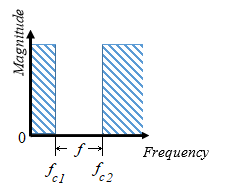
Band pass — Allows signals, $f$ , only in the range of frequencies between two cutoff frequencies, $f_{c 1}$ and $f_{c 2}$ , to pass.
Band stop — Prevents signals, $f$ , only in the range of frequencies between two cutoff frequencies, $f_{c 1}$ and $f_{c 2}$ , from passing.

Filter Type	Frequency Range, $f$
Low-Pass		$f < f_{c}$
High-Pass		$f > f_{c}$
Band-Pass		$f_{c 1} < f < f_{c 2}$
Band-Stop		$f_{c 1} < f < f_{c 2}$

Equations

The second order derivative state equation for the filter is:

$\frac{d^{2} x}{d t^{2}} = u - 2 ζ ω_{n} \frac{d x}{d t} - ω_{n}^{2} x$

Where:

x is the filter internal state.
u is the filter input.
ω_n is the filter natural frequency.
ζ is the filter damping factor.

For each filter type, the table maps the block output, $y (x)$ , as a function of the internal state of the filter, to the s-domain transfer function, $G (s)$ .

Filter Type	Output, $y (x)$	Transfer Function, $G (s)$
Low-Pass	$ω_{n}^{2} x$	$\frac{ω_{n}^{2}}{s^{2} + 2 ζ ω_{n} s + ω_{n}^{2}}$
High-Pass	$\frac{d^{2} x}{d t^{2}}$	$\frac{s^{2}}{s^{2} + 2 ζ ω_{n} s + ω_{n}^{2}}$
Band-Pass	$2 ζ ω_{n} \frac{d x}{d t}$	$\frac{2 ζ ω_{n} s}{s^{2} + 2 ζ ω_{n} s + ω_{n}^{2}}$
Band-Stop	$\frac{d^{2} x}{d t^{2}} + x$	$\frac{s^{2} + ω_{n}^{2}}{s^{2} + 2 ζ ω_{n} s + ω_{n}^{2}}$

For Initialization:

$\dot{x} (0) = {\frac{d x}{d t} |}_{t = 0}$

$u (0) = u_{1} (0) + u_{2} (0)$

$u_{1} (0) = A_{0} e^{j φ_{0}}$

$u_{2} (0) = b_{0} e^{j \frac{π}{2}}$

Where:

$x (0)$ is the initial state of the filter.
$u (0)$ is the initial input to the filter.
$u_{1} (0)$ is the AC component of the steady-state initial input.
$A_{0}$ is the initial amplitude.
$φ_{0}$ is the initial phase.
$u_{2} (0)$ is the DC component of the steady-state initial input.
$b_{0}$ is the initial bias.

In the s-domain $s = j ω_{0}$ . Therefore, for the initial frequency, $ω_{0}$ :

$\dot{x} (0) = I m (\frac{j ω_{0} u_{1} (0)}{- ω_{0}^{2} + j ω_{0} 2 ζ ω_{n} + ω_{n}^{2}}) .$

$x (0) = I m (\frac{\dot{x} (0) ω_{n}^{2}}{j ω_{0}} + u_{2} (0))$

Ports

Input

expand all

u — Filter input
scalar

Filter input.

Data Types: single | double

fn — Natural frequency
scalar

Natural frequency.

Data Types: single | double

Output

expand all

y — Filtered output
scalar

Filtered output.

Data Types: single | double

Parameters

expand all

Main

Filter type — Filter type
`Low-pass` (default) | `High-pass` | `Band-pass` | `Band-stop`

Type of second-order filter.

Initial natural frequency (Hz) — Initial natural frequency
`60` (default) | positive scalar

Natural frequency, in Hz, at the start of simulation.

Initial Conditions

Damping factor — Damping factor
`0.707` (default) | nonnegative scalar

Damping factor of the filter.

Sample time (-1 for inherited) — Block sample time
`-1` (default) | `0` | positive scalar

Time between consecutive block executions. During execution, the block produces outputs and, if appropriate, updates its internal state. For more information, see What Is Sample Time? and Specify Sample Time.

For inherited discrete-time operation, set this parameter to -1. For discrete-time operation, set this parameter to a positive integer. For continuous-time operation, set this parameter to 0.

If this block is in a masked subsystem or a variant subsystem that supports switching between continuous operation and discrete operation, promote this parameter to ensure correct switching between the continuous and discrete implementations of the block. For more information, see Promote Block Parameters on a Mask.

Initial amplitude — Initial amplitude
`0` (default) | nonnegative scalar

Amplitude at the start of simulation.

Initial phase (rad) — Initial phase
`0` (default) | nonnegative scalar

Phase, in rad, at the start of simulation.

Initial frequency (Hz) — Initial frequency
`0` (default) | scalar

Frequency, in Hz, at the start of simulation.

Initial bias — Initial bias
`0` (default) | nonnegative scalar

Bias at the start of simulation.

References

[1] Agarwal, A. and Lang, J. H. Foundations of Analog and Digital Electronic Circuits. New York: Elsevier, 2005.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2018b

Variable-Frequency Second-Order Filter

Description

Equations

Ports

Input

u — Filter input scalar

fn — Natural frequency scalar

Output

y — Filtered output scalar

Parameters

Main

Filter type — Filter type Low-pass (default) | High-pass | Band-pass | Band-stop

Initial natural frequency (Hz) — Initial natural frequency 60 (default) | positive scalar

Initial Conditions

Damping factor — Damping factor 0.707 (default) | nonnegative scalar

Sample time (-1 for inherited) — Block sample time -1 (default) | 0 | positive scalar

Initial amplitude — Initial amplitude 0 (default) | nonnegative scalar

Initial phase (rad) — Initial phase 0 (default) | nonnegative scalar

Initial frequency (Hz) — Initial frequency 0 (default) | scalar

Initial bias — Initial bias 0 (default) | nonnegative scalar

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

See Also

u — Filter input
scalar

fn — Natural frequency
scalar

y — Filtered output
scalar

Filter type — Filter type
`Low-pass` (default) | `High-pass` | `Band-pass` | `Band-stop`

Initial natural frequency (Hz) — Initial natural frequency
`60` (default) | positive scalar

Damping factor — Damping factor
`0.707` (default) | nonnegative scalar

Sample time (-1 for inherited) — Block sample time
`-1` (default) | `0` | positive scalar

Initial amplitude — Initial amplitude
`0` (default) | nonnegative scalar

Initial phase (rad) — Initial phase
`0` (default) | nonnegative scalar

Initial frequency (Hz) — Initial frequency
`0` (default) | scalar

Initial bias — Initial bias
`0` (default) | nonnegative scalar

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.