Main Content

disparateImpactRemover

Remove disparate impact of sensitive attribute

Since R2022b

expand all in page

    Description

    To try to create fairness in binary classification, you can use the disparateImpactRemover function to remove or reduce the disparate impact of a sensitive attribute. Before training your model, use the sensitive attribute to transform the continuous predictors in the training data set. The function returns the transformed data set and a disparateImpactRemover object that contains the transformation. Pass the transformed data set to an appropriate training function, such as fitcsvm, and pass the object to the transform object function to apply the transformation to a new data set, such as a test data set.

    Note

    You must transform new data, such as test data, after training a model using disparateImpactRemover. Otherwise, the predicted results are inaccurate.

    Creation

    Syntax

    remover = disparateImpactRemover(Tbl,AttributeName)
    [remover,transformedData] = disparateImpactRemover(Tbl,AttributeName)
    [remover,transformedData] = disparateImpactRemover(X,attribute)
    [remover,transformedData] = disparateImpactRemover(___,Name=Value)

    Description

    remover = disparateImpactRemover(Tbl,AttributeName) removes the disparate impact of the AttributeName sensitive attribute in the table Tbl by transforming the continuous predictors in the data set Tbl. The returned disparateImpactRemover object (remover) stores the transformation, which you can apply to new data. For more information, see Algorithms.

    [remover,transformedData] = disparateImpactRemover(Tbl,AttributeName) also returns the transformed predictor data transformedData, which corresponds to the data in Tbl.

    Note that transformedData includes the sensitive attribute in this syntax. After using disparateImpactRemover, avoid using the sensitive attribute as a separate predictor when training your model.

    example

    [remover,transformedData] = disparateImpactRemover(X,attribute) uses the numeric predictor data X and the sensitive attribute specified by attribute to transform the predictors.

    example

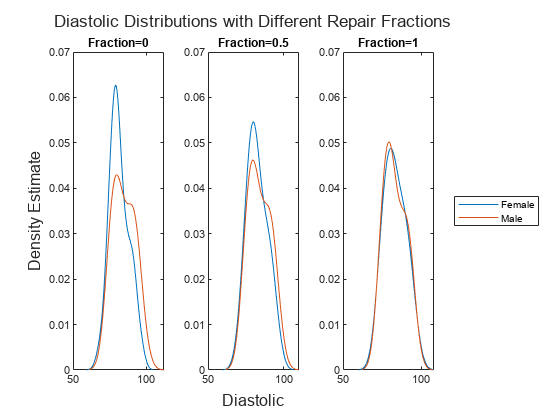
    [remover,transformedData] = disparateImpactRemover(___,Name=Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in previous syntaxes. For example, you can specify the extent of the data transformation by using the RepairFraction name-value argument. A value of 1 indicates a full transformation, and a value of 0 indicates no transformation.

    example

    Input Arguments

    expand all

    Data set, specified as a table. Each row of Tbl corresponds to one observation, and each column corresponds to one variable. When you use a table with disparateImpactRemover, the table must include the sensitive attribute. The table can include additional variables, such as the response variable. Multicolumn variables and cell arrays other than cell arrays of character vectors are not allowed.

    If Tbl contains numeric variables that you want disparateImpactRemover to ignore (such as observation weights), you can specify the continuous numeric variables to transform by using the PredictorNames name-value argument.

    Data Types: table

    Sensitive attribute name, specified as the name of a variable in Tbl. You must specify AttributeName as a character vector or a string scalar. For example, if the sensitive attribute is stored as Tbl.Attribute, then specify it as "Attribute".

    The sensitive attribute must be a numeric vector, logical vector, character array, string array, cell array of character vectors, or categorical vector.

    Data Types: char | string

    Predictor data, specified as a numeric matrix. Each row of X corresponds to one observation, and each column corresponds to one predictor variable. X and attribute must have the same number of rows.

    To specify the names of the predictors in the order of their appearance in X, use the PredictorNames name-value argument.

    Data Types: single | double

    Sensitive attribute, specified as a numeric column vector, logical column vector, character array, string array, cell array of character vectors, or categorical column vector.

    • If attribute is an array, then each row of the array must correspond to a group in the sensitive attribute.

    • attribute and X must have the same number of rows.

    Data Types: single | double | logical | char | string | cell | categorical

    Name-Value Arguments

    Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

    Example: disparateImpactRemover(Tbl,"Age",PredictorNames=["Diastolic","Systolic"]) specifies to transform the Diastolic and Systolic variables in the table Tbl by using the Age sensitive attribute in Tbl.

    Names of the predictor variables to transform, specified as a string array of unique names or cell array of unique character vectors.

    • If you supply Tbl, then you can use PredictorNames to specify which numeric predictor variables to transform.

    • If you supply X, then you can use PredictorNames to assign names to the predictor variables in X.

    Example: PredictorNames=["SepalLength","SepalWidth","PetalLength","PetalWidth"]

    Data Types: string | cell

    Fraction of the data transformation, specified as a numeric scalar in the range [0,1]. A value of 1 indicates a full transformation, and a value of 0 indicates no transformation.

    A greater repair fraction can result in a greater loss in model prediction accuracy. For more information, see [1].

    Example: RepairFraction=0.5

    Data Types: single | double

    Output Arguments

    expand all

    Predictor data transformer, returned as a disparateImpactRemover object. remover contains the transformation of the remover.PredictorNames predictor variables with respect to the remover.SensitiveAttribute variable.

    Transformed predictor data corresponding to the data in Tbl or X, returned as a table or numeric matrix. Note that transformedData can include the sensitive attribute. After you use the disparateImpactRemover function, avoid using the sensitive attribute as a separate predictor when training your model.

    Properties

    expand all

    This property is read-only.

    Fraction of the data transformation, returned as a numeric scalar in the range [0,1]. A value of 1 indicates a full transformation, and a value of 0 indicates no transformation.

    If you want to adjust the repair fraction after creating a disparateImpactRemover object, specify the RepairFraction name-value argument of the transform object function.

    Data Types: single | double

    This property is read-only.

    Names of the transformed predictor variables, returned as a cell array of unique character vectors. The order of the elements of PredictorNames corresponds to the order in which the predictor names appear in the Tbl or X data.

    Data Types: cell

    This property is read-only.

    Sensitive attribute, returned as a variable name, numeric column vector, logical column vector, character array, cell array of character vectors, or categorical column vector.

    • If you use a table to create the disparateImpactRemover object, then SensitiveAttribute is the name of the sensitive attribute. The name is stored as a character vector.

    • If you use a matrix to create the disparateImpactRemover object, then SensitiveAttribute has the same size and data type as the sensitive attribute used to create the object. (The software treats string arrays as cell arrays of character vectors.)

    Data Types: single | double | logical | char | cell | categorical

    Object Functions

    transformTransform new predictor data to remove disparate impact

    Examples

    collapse all

    Open Live Script

    Train a binary classifier, classify test data using the model, and compute the disparate impact for each group in the sensitive attribute. To reduce the disparate impact values, use disparateImpactRemover, and then retrain the binary classifier. Transform the test data set, reclassify the observations, and compute the disparate impact values.

    Load the sample data census1994, which contains the training data adultdata and the test data adulttest. The data sets consist of demographic information from the US Census Bureau that can be used to predict whether an individual makes over $50,000 per year. Preview the first few rows of the training data set.

    load census1994
head(adultdata)
        age       workClass          fnlwgt      education    education_num       marital_status           occupation        relationship     race      sex      capital_gain    capital_loss    hours_per_week    native_country    salary
    ___    ________________    __________    _________    _____________    _____________________    _________________    _____________    _____    ______    ____________    ____________    ______________    ______________    ______

    39     State-gov                77516    Bachelors         13          Never-married            Adm-clerical         Not-in-family    White    Male          2174             0                40          United-States     <=50K 
    50     Self-emp-not-inc         83311    Bachelors         13          Married-civ-spouse       Exec-managerial      Husband          White    Male             0             0                13          United-States     <=50K 
    38     Private             2.1565e+05    HS-grad            9          Divorced                 Handlers-cleaners    Not-in-family    White    Male             0             0                40          United-States     <=50K 
    53     Private             2.3472e+05    11th               7          Married-civ-spouse       Handlers-cleaners    Husband          Black    Male             0             0                40          United-States     <=50K 
    28     Private             3.3841e+05    Bachelors         13          Married-civ-spouse       Prof-specialty       Wife             Black    Female           0             0                40          Cuba              <=50K 
    37     Private             2.8458e+05    Masters           14          Married-civ-spouse       Exec-managerial      Wife             White    Female           0             0                40          United-States     <=50K 
    49     Private             1.6019e+05    9th                5          Married-spouse-absent    Other-service        Not-in-family    Black    Female           0             0                16          Jamaica           <=50K 
    52     Self-emp-not-inc    2.0964e+05    HS-grad            9          Married-civ-spouse       Exec-managerial      Husband          White    Male             0             0                45          United-States     >50K

    Each row contains the demographic information for one adult. The last column salary shows whether a person has a salary less than or equal to $50,000 per year or greater than $50,000 per year.

    Remove observations from adultdata and adulttest that contain missing values.

    adultdata = rmmissing(adultdata);
adulttest = rmmissing(adulttest);

    Specify the continuous numeric predictors to use for model training.

    predictors = ["age","education_num","capital_gain","capital_loss", ...
    "hours_per_week"];

    Train an ensemble classifier using the training set adultdata. Specify salary as the response variable and fnlwgt as the observation weights. Because the training set is imbalanced, use the RUSBoost algorithm. After training the model, predict the salary (class label) of the observations in the test set adulttest.

    rng("default") % For reproducibility
mdl = fitcensemble(adultdata,"salary",Weights="fnlwgt", ...
    PredictorNames=predictors,Method="RUSBoost");
labels = predict(mdl,adulttest);

    Transform the training set predictors by using the race sensitive attribute.

    [remover,newadultdata] = disparateImpactRemover(adultdata, ...
    "race",PredictorNames=predictors);
remover
    remover = 
  disparateImpactRemover with properties:

        RepairFraction: 1
        PredictorNames: {'age'  'education_num'  'capital_gain'  'capital_loss'  'hours_per_week'}
    SensitiveAttribute: 'race'

    remover is a disparateImpactRemover object, which contains the transformation of the remover.PredictorNames predictors with respect to the remover.SensitiveAttribute variable.

    Apply the same transformation stored in remover to the test set predictors. Note: You must transform both the training and test data sets before passing them to a classifier.

    newadulttest = transform(remover,adulttest, ...
    PredictorNames=predictors);

    Train the same type of ensemble classifier as mdl, but use the transformed predictor data. As before, predict the salary (class label) of the observations in the test set adulttest.

    rng("default") % For reproducibility
newMdl = fitcensemble(newadultdata,"salary",Weights="fnlwgt", ...
    PredictorNames=predictors,Method="RUSBoost");
newLabels = predict(newMdl,newadulttest);

    Compare the disparate impact values for the predictions made by the original model (mdl) and the predictions made by the model trained with the transformed data (newMdl). For each group in the sensitive attribute, the disparate impact value is the proportion of predictions in that group with a positive class value (pg+) divided by the proportion of predictions in the reference group with a positive class value (pr+). An ideal classifier makes predictions where, for each group, pg+ is close to pr+ (that is, where the disparate impact value is close to 1).

    Compute the disparate impact values for the mdl predictions and the newMdl predictions by using fairnessMetrics. Include the observation weights. You can use the report object function to display bias metrics, such as disparate impact, that are stored in the evaluator object.

    evaluator = fairnessMetrics(adulttest,"salary", ...
    SensitiveAttributeNames="race",Predictions=[labels,newLabels], ...
    Weights="fnlwgt",ModelNames=["Original Model","New Model"]);
evaluator.PositiveClass
    ans = categorical
     >50K 


    evaluator.ReferenceGroup
    ans = 
'White'

    report(evaluator,BiasMetrics="DisparateImpact")
    ans=5×5 table
        Metrics        SensitiveAttributeNames          Groups          Original Model    New Model
    _______________    _______________________    __________________    ______________    _________

    DisparateImpact             race              Amer-Indian-Eskimo       0.41702         0.92804 
    DisparateImpact             race              Asian-Pac-Islander         1.719          0.9697 
    DisparateImpact             race              Black                    0.60571         0.66629 
    DisparateImpact             race              Other                    0.66958         0.86039 
    DisparateImpact             race              White                          1               1

    For the mdl predictions, several of the disparate impact values are below the industry standard of 0.8, and one value is above 1.25. These values indicate bias in the predictions with respect to the positive class >50K and the sensitive attribute race.

    The disparate impact values for the newMdl predictions are closer to 1 than the disparate impact values for the mdl predictions. One value is still below 0.8.

    Visually compare the disparate impact values by using the bar graph returned by the plot object function.

    plot(evaluator,"DisparateImpact")

    Figure contains an axes object. The axes object with title Disparate Impact, xlabel Fairness Metric Value, ylabel race contains 2 objects of type bar. These objects represent Original Model, New Model.

    The disparateImpactRemover function seems to have improved the model predictions on the test set with respect to the disparate impact metric.

    Check whether the transformed predictors negatively affect the accuracy of the model predictions. Compute the accuracy of the test set predictions for the two models mdl and newMdl.

    accuracy = 1-loss(mdl,adulttest,"salary")
    accuracy = 
0.8024

    newAccuracy = 1-loss(newMdl,newadulttest,"salary")
    newAccuracy = 
0.7955

    The model trained using the transformed predictors (newMdl) achieves similar test set accuracy compared to the model trained with the original predictors (mdl).

    Open Live Script

    Try to remove the disparate impact of a sensitive attribute by adjusting continuous numeric predictors. Visualize the difference between the original and adjusted predictor values.

    Suppose you want to create a binary classifier that predicts whether a patient is a smoker based on the patient's diastolic and systolic blood pressure values. Also, you want to remove the disparate impact of the patient's gender on model predictions. Before training the model, you can use disparateImpactRemover to transform the continuous predictor variables in your data set.

    Load the patients data set, which contains medical information for 100 patients. Convert the Gender and Smoker variables to categorical variables. Specify the descriptive category names Smoker and Nonsmoker rather than 1 and 0.

    load patients
Gender = categorical(Gender);
Smoker = categorical(Smoker,logical([1 0]), ...
    ["Smoker","Nonsmoker"]);

    Create a matrix containing the continuous predictors Diastolic and Systolic.

    X = [Diastolic,Systolic];

    Find the observations in the two groups of the sensitive attribute Gender.

    femaleIdx = Gender=="Female";
maleIdx = Gender=="Male";
femaleX = X(femaleIdx,:);
maleX = X(maleIdx,:);

    Compute the Diastolic and Systolic quantiles for the two groups in the sensitive attribute. Specify the number of quantiles to be the minimum number of group observations across the groups in the sensitive attribute, provided that the number is smaller than 100.

    t = tabulate(Gender);
t = array2table(t,VariableNames=["Value","Count","Percent"])
    t=2×3 table
      Value       Count     Percent
    __________    ______    _______

    {'Female'}    {[53]}    {[53]} 
    {'Male'  }    {[47]}    {[47]} 


    numQuantiles = min(100,min(t.Count{:}))
    numQuantiles = 
47

    femaleQuantiles = quantile(femaleX,numQuantiles,1);
maleQuantiles = quantile(maleX,numQuantiles,1);

    Compute the median quantiles across the two groups.

    Q(:,:,1) = femaleQuantiles;
Q(:,:,2) = maleQuantiles;
medianQuantiles = median(Q,3);

    Plot the results. Show the Diastolic quantiles in the left plot and the Systolic quantiles in the right plot.

    tiledlayout(1,2)

nexttile % Diastolic
plot(femaleQuantiles(:,1),1:numQuantiles)
hold on
plot(maleQuantiles(:,1),1:numQuantiles)
plot(medianQuantiles(:,1),1:numQuantiles)
hold off
xlabel("Diastolic")
ylabel("Quantile")
legend(["Female","Male","Median"],Location="southeast")

nexttile % Systolic
plot(femaleQuantiles(:,2),1:numQuantiles)
hold on
plot(maleQuantiles(:,2),1:numQuantiles)
plot(medianQuantiles(:,2),1:numQuantiles)
hold off
xlabel("Systolic")
ylabel("Quantile")
legend(["Female","Male","Median"],Location="southeast")

    Figure contains 2 axes objects. Axes object 1 with xlabel Diastolic, ylabel Quantile contains 3 objects of type line. These objects represent Female, Male, Median. Axes object 2 with xlabel Systolic, ylabel Quantile contains 3 objects of type line. These objects represent Female, Male, Median.

    For each predictor, the Female and Male quantiles differ. The disparateImpactRemover function uses the median quantiles to adjust this difference.

    Transform the Diastolic and Systolic predictors in X by using the Gender sensitive attribute.

    [remover,newX] = disparateImpactRemover(X,Gender);
femaleNewX = newX(femaleIdx,:);
maleNewX = newX(maleIdx,:);

    Visualize the difference in the Diastolic distributions between the original values in X and the transformed values in newX. Compute and display the probability density estimates by using the ksdensity function.

    tiledlayout(1,2)

nexttile
ksdensity(femaleX(:,1))
hold on
ksdensity(maleX(:,1))
hold off
xlabel("Diastolic")
ylabel("Probability Density Estimate")
title("Original")
legend(["Female","Male"])
ylim([0,0.07])

nexttile
ksdensity(femaleNewX{:,1})
hold on
ksdensity(maleNewX{:,1})
hold off
xlabel("Diastolic")
ylabel("Probability Density Estimate")
title("Transformed")
legend(["Female","Male"])
ylim([0,0.07])

    Figure contains 2 axes objects. Axes object 1 with title Original, xlabel Diastolic, ylabel Probability Density Estimate contains 2 objects of type line. These objects represent Female, Male. Axes object 2 with title Transformed, xlabel Diastolic, ylabel Probability Density Estimate contains 2 objects of type line. These objects represent Female, Male.

    The disparateImpactRemover function transforms the values in the Diastolic predictor variable so that the distribution of Female values and the distribution of Male values are similar.

    You can now train a binary classifier using the adjusted predictor data. For this example, train a tree classifier.

    tree = fitctree(newX,Smoker)
    tree = 
  ClassificationTree
           PredictorNames: {'x1'  'x2'}
             ResponseName: 'Y'
    CategoricalPredictors: []
               ClassNames: [Smoker    Nonsmoker]
           ScoreTransform: 'none'
          NumObservations: 100

    Note: You must transform new data sets before passing them to the classifier for prediction.

    Randomly sample 10 observations from X. Transform the values using the remover object and the transform object function. Then, predict the smoker status for the observations.

    rng("default") % For reproducibility
testIdx = randsample(size(X,1),10,1);
testX = transform(remover,X(testIdx,:),Gender(testIdx));
label = predict(tree,testX)
    label = 10x1 categorical
     Nonsmoker 
     Smoker 
     Nonsmoker 
     Nonsmoker 
     Nonsmoker 
     Nonsmoker 
     Nonsmoker 
     Smoker 
     Smoker 
     Smoker
    Open Live Script

    Specify the extent of the transformation of the continuous numeric predictors with respect to a sensitive attribute. Use the RepairFraction name-value argument of the disparateImpactRemover function.

    Load the patients data set, which contains medical information for 100 patients. Convert the Gender and Smoker variables to categorical variables. Specify the descriptive category names Smoker and Nonsmoker rather than 1 and 0.

    load patients
Gender = categorical(Gender);
Smoker = categorical(Smoker,logical([1 0]), ...
    ["Smoker","Nonsmoker"]);

    Create a matrix containing the continuous predictors Diastolic and Systolic.

    X = [Diastolic,Systolic];

    Find the observations in the two groups of the sensitive attribute Gender.

    femaleIdx = Gender=="Female";
maleIdx = Gender=="Male";
femaleX = X(femaleIdx,:);
maleX = X(maleIdx,:);

    Transform the Diastolic and Systolic predictors in X by using the Gender sensitive attribute. Specify a repair fraction of 0.5. Note that a value of 1 indicates a full transformation, and a value of 0 indicates no transformation.

    [remover,newX50] = disparateImpactRemover(X,Gender, ...
    RepairFraction=0.5);
femaleNewX50 = newX50(femaleIdx,:);
maleNewX50 = newX50(maleIdx,:);

    Fully transform the predictor variables by using the transform object function of the remover object.

    newX100 = transform(remover,X,Gender,RepairFraction=1);
femaleNewX100 = newX100(femaleIdx,:);
maleNewX100 = newX100(maleIdx,:);

    Visualize the difference in the Diastolic distributions between the original values in X, the partially repaired values in newX50, and the fully transformed values in newX100. Compute and display the probability density estimates by using the ksdensity function.

    t = tiledlayout(1,3);
title(t,"Diastolic Distributions with Different " + ...
    "Repair Fractions")
xlabel(t,"Diastolic")
ylabel(t,"Density Estimate")

nexttile
ksdensity(femaleX(:,1))
hold on
ksdensity(maleX(:,1))
hold off
title("Fraction=0")
ylim([0,0.07])

nexttile
ksdensity(femaleNewX50{:,1})
hold on
ksdensity(maleNewX50{:,1})
hold off
title("Fraction=0.5")
ylim([0,0.07])

nexttile
ksdensity(femaleNewX100{:,1})
hold on
ksdensity(maleNewX100{:,1})
hold off
title("Fraction=1")
ylim([0,0.07])
legend(["Female","Male"],Location="eastoutside")

    Figure contains 3 axes objects. Axes object 1 with title Fraction=0 contains 2 objects of type line. Axes object 2 with title Fraction=0.5 contains 2 objects of type line. Axes object 3 with title Fraction=1 contains 2 objects of type line. These objects represent Female, Male.

    As the repair fraction increases, the disparateImpactRemover function transforms the values in the Diastolic predictor variable so that the distribution of Female values and the distribution of Male values become more similar.

    More About

    expand all

    Tips

    • After using disparateImpactRemover, consider using only continuous and ordinal predictors for model training. Avoid using the sensitive attribute as a separate predictor when training your model. For more information, see [1].

    • You must transform new data, such as test data, after training a model using disparateImpactRemover. Otherwise, the predicted results are inaccurate. Use the transform object function.

    Algorithms

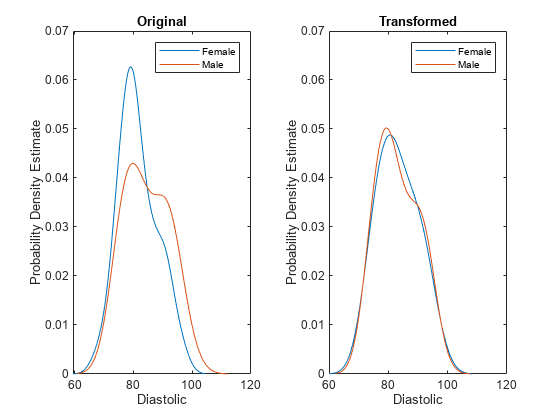
    disparateImpactRemover transforms a continuous predictor in Tbl or X as follows:

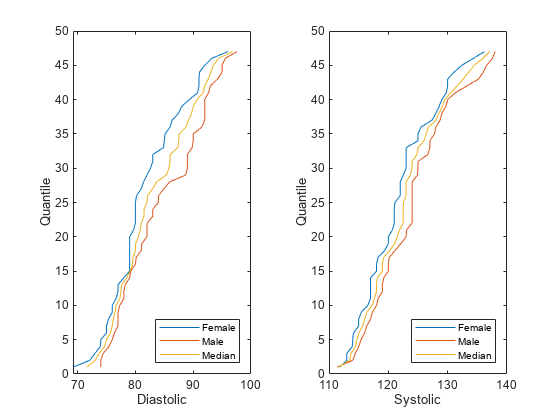
    1. The software uses the groups in the sensitive attribute to split the predictor values. For each group g, the software computes q quantiles of the predictor values by using the quantile function. The number of quantiles q is either 100 or the minimum number of group observations across the groups in the sensitive attribute, whichever is smaller. The software creates a corresponding binning function Fg using the discretize function and the quantile values as bin edges.

    2. The software then finds the median quantile values across all the sensitive attribute groups and forms the associated quantile function Fm-1. The software omits missing (NaN) values from this calculation.

    3. Finally, the software transforms the predictor value x in the sensitive attribute group g by using the transformation λFm-1(Fg(x)) + (1 – λ)x, where λ is the repair fraction RepairFraction. The software preserves missing (NaN) values in the predictor.

    The function stores the transformation, which you can apply to new predictor data.

    For more information, see [1].

    References

    [1] Feldman, Michael, Sorelle A. Friedler, John Moeller, Carlos Scheidegger, and Suresh Venkatasubramanian. “Certifying and Removing Disparate Impact.” In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 259–68. Sydney NSW Australia: ACM, 2015. https://doi.org/10.1145/2783258.2783311.

    Version History

    Introduced in R2022b

    See Also

    | |

    Topics