quantile

数据集的分位数

全页折叠

语法

Q = quantile(A,p)

Q = quantile(A,n)

Q = quantile(___,"all")

Q = quantile(___,dim)

Q = quantile(___,vecdim)

Q = quantile(___,Method=method)

说明

Q = quantile(A,p) 返回输入数据 A 中元素在区间 [0,1] 上累积概率 p 下的分位数。

如果 A 是向量，则 Q 是标量或与 p 长度相同的向量。Q(i) 包含 p(i) 分位数。
如果 A 是矩阵，则 Q 是行向量或矩阵，其中 Q 的行数等于 length(p)。Q 的第 i 行包含 A 的每列的 p(i) 分位数。
如果 A 是多维数组，则 Q 包含沿其大小不等于 1 的第一个数组维度计算的分位数。

示例

Q = quantile(A,n) 返回 n 个等间距累积概率对应的分位数（1/(n + 1)，2/(n + 1)，...，n/(n + 1)，其中整数 n > 1）。

如果 A 是向量，则 Q 是标量或长度为 n 的向量。
如果 A 是矩阵，则 Q 是具有 n 行的矩阵。
如果 A 是多维数组，则 Q 包含沿其大小不等于 1 的第一个数组维度计算的分位数。

示例

对于前两个语法中的任一个，Q = quantile(___,"all") 返回 A 的所有元素的分位数。

示例

对于前两个语法中的任一个，Q = quantile(___,dim) 沿维度 dim 执行运算。例如，如果 A 是矩阵，则 quantile(A,p,2) 对每行中的元素执行运算。

示例

对于前两个语法中的任一个，Q = quantile(___,vecdim) 沿在向量 vecdim 中指定的维度执行运算。例如，如果 A 是矩阵，则 quantile(A,n,[1 2]) 对 A 的所有元素执行运算，因为矩阵的每个元素都包含在由维度 1 和 2 定义的数组切片中。

示例

Q = quantile(___,Method=method) 使用指定的方法计算分位数。除了上述语法中的任何输入参量组合之外，还需要指定方法。

示例

全部折叠

给定概率的分位数

打开实时脚本

计算数据集在指定概率下的分位数。

生成一个大小为 7 的数据集。

rng default % for reproducibility
A = randn(1,7)

A = 1×7

    0.5377    1.8339   -2.2588    0.8622    0.3188   -1.3077   -0.4336

计算 A 的元素的 0.3 分位数。

Q = quantile(A,0.3)

Q = 
-0.7832

计算 A 的元素在累积概率 0.025、0.25、0.5、0.75 和 0.975 下的分位数。

Q = quantile(A,[0.025 0.25 0.5 0.75 0.975])

Q = 1×5

   -2.2588   -1.0892    0.3188    0.7810    1.8339

`n` 个等间距累积概率对应的分位数

打开实时脚本

计算数据集在给定数量的概率下的分位数。

生成一个大小为 7 的数据集。

rng default % for reproducibility
A = randn(1,7)

A = 1×7

    0.5377    1.8339   -2.2588    0.8622    0.3188   -1.3077   -0.4336

计算 A 的元素的四个等间距分位数。

Q = quantile(A,4)

Q = 1×4

   -1.4028   -0.2079    0.4720    0.9593

使用 Q = quantile(A,[0.2,0.4,0.6,0.8]) 是返回四个等间距分位数的另一种方式。

矩阵在给定概率下的分位数

打开实时脚本

计算指定概率下沿数据矩阵的列和行的分位数。

生成一个 4×6 数据矩阵。

rng default % for reproducibility
A = randn(4,6)

A = 4×6

    0.5377    0.3188    3.5784    0.7254   -0.1241    0.6715
    1.8339   -1.3077    2.7694   -0.0631    1.4897   -1.2075
   -2.2588   -0.4336   -1.3499    0.7147    1.4090    0.7172
    0.8622    0.3426    3.0349   -0.2050    1.4172    1.6302

计算 A 的每列的 0.3 分位数。

Q = quantile(A,0.3,1)

Q = 1×6

   -0.3013   -0.6958    1.5336   -0.1056    0.9491    0.1078

当计算 A 中每列的 1 分位数时，quantile 返回行向量 Q。-0.3013 是 A 的第一列（元素为 0.5377、1.8339、-2.2588 和 0.8622）的 0.3 分位数。由于 dim 的默认值为 1，Q = quantile(A,0.3) 返回相同的结果。

计算 A 的每行的 0.3 分位数。

Q = quantile(A,0.3,2)

当计算 A 中每行的一个分位数时，quantile 返回列向量 Q。0.3844 是 A 的第一行（元素为 0.5377、0.3188、3.5784、0.7254、-0.1241 和 0.6715）的 0.3 分位数。

矩阵在 `n` 个等间距概率下的分位数

打开实时脚本

计算沿数据矩阵的列和行的等间距分位数。

生成一个 6×7 数据矩阵。

rng default % for reproducibility
A = randi(10,6,7)

A = 6×7

     9     3    10     8     7     8     7
    10     6     5    10     8     1     4
     2    10     9     7     8     3    10
    10    10     2     1     4     1     1
     7     2     5     9     7     1     5
     1    10    10    10     2     9     4

计算 A 的每列在三个等间距累积概率下的分位数。

Q = quantile(A,3,1)

Q = 3×7

    2.0000    3.0000    5.0000    7.0000    4.0000    1.0000    4.0000
    8.0000    8.0000    7.0000    8.5000    7.0000    2.0000    4.5000
   10.0000   10.0000   10.0000   10.0000    8.0000    8.0000    7.0000

矩阵 Q 的每列包含 A 中对应列的分位数。2、8 和 10 是 A 的第一列（元素为 9、10、2、10、7 和 1）的分位数。Q = quantile(A,3) 返回相同的结果，因为 dim 的默认值为 1。

计算 A 的每行在三个等间距累积概率下的分位数。

Q = quantile(A,3,2)

Q = 6×3

    7.0000    8.0000    8.7500
    4.2500    6.0000    9.5000
    4.0000    8.0000    9.7500
    1.0000    2.0000    8.5000
    2.7500    5.0000    7.0000
    2.5000    9.0000   10.0000

矩阵 Q 的每行包含 A 中对应行的三个等间距分位数。7、8 和 8.75 是 A 的第一行（元素为 9、3、10、8、7、8 和 7）的分位数。

多维数组在给定概率下的分位数

打开实时脚本

使用 "all" 和 vecdim 输入计算多维数组在指定概率下的分位数。

创建一个 3×5×2 数组。指定一个概率向量。

A = reshape(1:30,[3 5 2])

A = 
A(:,:,1) =

     1     4     7    10    13
     2     5     8    11    14
     3     6     9    12    15


A(:,:,2) =

    16    19    22    25    28
    17    20    23    26    29
    18    21    24    27    30

p = [0.25 0.75];

计算 A 的所有元素的 0.25 和 0.75 分位数。

Qall = quantile(A,p,"all")

Qall = 2×1

     8
    23

Qall(1) 是 A 的 0.25 分位数，Qall(2) 是 A 的 0.75 分位数。

通过指定维度 1 和 2 作为运算维度，计算 A 的每页的 0.25 和 0.75 分位数。

Qpage = quantile(A,p,[1 2])

Qpage = 
Qpage(:,:,1) =

    4.2500
   11.7500


Qpage(:,:,2) =

   19.2500
   26.7500

Qpage(1,1,1) 是 A 的第一页的 0.25 分位数，Qpage(2,1,1) 是 A 的第一页的 0.75 分位数。

通过指定维度 2 和 3 作为运算维度，计算每个 A(i,:,:) 切片中元素的 0.25 和 0.75 分位数。

Qrow = quantile(A,p,[2 3])

Qrow(3,1) 是 A(3,:,:) 中元素的 0.25 分位数，Qrow(3,2) 是 A(3,:,:) 中元素的 0.75 分位数。

偶数个数据元素的中位数和四分位数

打开实时脚本

查找具有偶数个元素的向量的中位数和四分位数。

创建一个数据向量。

A = [2 5 6 10 11 13]

A = 1×6

     2     5     6    10    11    13

计算 A 的元素的中位数。

Q = quantile(A,0.5)

Q = 
8

计算 A 的元素的四分位数。

Q = quantile(A,[0.25, 0.5, 0.75])

Q = 1×3

     5     8    11

使用 Q = quantile(A,3) 是计算 A 的元素的四分位数的另一种方式。

这些结果可能与教科书定义不同，因为 quantile 使用线性插值来查找中位数和四分位数。

奇数个数据元素的中位数和四分位数

打开实时脚本

查找具有奇数个元素的向量的中位数和四分位数。

创建一个数据向量。

A = [2 4 6 8 10 12 14]

A = 1×7

     2     4     6     8    10    12    14

计算 A 的元素的中位数。

Q = quantile(A,0.50)

Q = 
8

计算 A 的元素的四分位数。

Q = quantile(A,[0.25, 0.5, 0.75])

Q = 1×3

    4.5000    8.0000   11.5000

使用 Q = quantile(A,3) 是计算 A 的四分位数的另一种方式。

这些结果可能与教科书定义不同，因为 quantile 使用线性插值来查找中位数和四分位数。

tall 向量在给定概率下的分位数

打开实时脚本

计算 tall 列向量在给定概率下的精确和近似分位数。

对 tall 数组执行计算时，MATLAB® 或者使用并行池（如果有 Parallel Computing Toolbox™，则默认使用并行池），或者使用本地 MATLAB 会话。要在有 Parallel Computing Toolbox 时使用本地 MATLAB 会话运行示例，请使用 mapreducer 函数更改全局执行环境。

mapreducer(0)

为 airlinesmall 数据集创建数据存储。将 "NA" 值视为缺失数据，以便 datastore 用 NaN 值替换它们。指定使用 ArrTime 变量。

ds = datastore("airlinesmall.csv","TreatAsMissing","NA", ...
    "SelectedVariableNames","ArrTime");

基于数据存储创建一个 tall 表 tt，并将数据从 tall 表提取到 tall 向量 A 中。

tt = tall(ds)

tt =

  M×1 tall table

    ArrTime
    _______

      735  
     1124  
     2218  
     1431  
      746  
     1547  
     1052  
     1134  
       :
       :

A = tt{:,:}

A =

  M×1 tall double column vector

         735
        1124
        2218
        1431
         746
        1547
        1052
        1134
         :
         :

计算 A 在累积概率 p = 0.5 时的精确分位数。由于 A 是 tall 列向量且 p 是标量，因此 quantile 默认返回精确的分位数。

p = 0.5;
Qexact = quantile(A,p)

Qexact =

  tall double

    ?

Preview deferred. Learn more.

计算 A 在 p = 0.5 时的近似分位数。将 method 指定为 "approximate" 以使用基于 T-Digest 的逼近算法计算分位数。

Qapprox = quantile(A,p,Method="approximate")

Qapprox =

  M×N×... tall array

    ?    ?    ?    ...
    ?    ?    ?    ...
    ?    ?    ?    ...
    :    :    :
    :    :    :

Preview deferred. Learn more.

使用 gather 计算 tall 数组并将结果传入内存中。

[Qexact,Qapprox] = gather(Qexact,Qapprox)

Evaluating tall expression using the Local MATLAB Session:
- Pass 1 of 4: Completed in 1.1 sec
- Pass 2 of 4: Completed in 0.37 sec
- Pass 3 of 4: Completed in 0.7 sec
- Pass 4 of 4: Completed in 0.45 sec
Evaluation completed in 3.3 sec

Qexact = 
1522

Qapprox = 
1.5220e+03

精确分位数和近似分位数的值在所示的四位数字上相同。

tall 矩阵沿不同维度的分位数

打开实时脚本

计算 tall 矩阵在指定累积概率下沿不同维度的精确和近似分位数。

mapreducer(0)

创建一个 tall 矩阵 A，其中包含来自 airlinesmall 数据集且存储在 varnames 中的变量子集。有关从 tall 数组提取数据的步骤的详细信息，请参阅tall 向量在给定概率下的分位数。

varnames = ["ArrDelay","ArrTime","DepTime","ActualElapsedTime"];
ds = datastore("airlinesmall.csv","TreatAsMissing","NA", ...
    "SelectedVariableNames",varnames);
tt = tall(ds);
A = tt{:,varnames}

A =

  M×4 tall double matrix

           8         735         642          53
           8        1124        1021          63
          21        2218        2055          83
          13        1431        1332          59
           4         746         629          77
          59        1547        1446          61
           3        1052         928          84
          11        1134         859         155
          :          :            :           :
          :          :            :           :

当沿非 1 的维度运算时，quantile 函数仅计算精确分位数，以便它能够使用基于排序的算法（请参阅算法）高效执行计算，而不是使用基于 T-Digest 的逼近算法。

计算 A 在累积概率向量 p（0.25、0.5 和 0.75）下沿第二个维度的精确分位数。

p = [0.25 0.5 0.75];
Qexact = quantile(A,p,2)

Qexact =

  M×N×... tall array

    ?    ?    ?    ...
    ?    ?    ?    ...
    ?    ?    ?    ...
    :    :    :
    :    :    :

Preview deferred. Learn more.

当函数沿第一个维度运算且 p 是累积概率向量时，您必须使用基于 T-digest 的逼近算法计算分位数。如果使用基于排序的算法计算 tall 数组沿第一个维度的分位数，计算量会很大。

计算 A 在累积概率 0.25、0.5 和 0.75 下沿第一个维度的精确分位数。由于默认维度是 1，因此无需为 dim 指定值。

Qapprox = quantile(A,p,Method="approximate")

Qapprox =

  M×N×... tall array

    ?    ?    ?    ...
    ?    ?    ?    ...
    ?    ?    ?    ...
    :    :    :
    :    :    :

Preview deferred. Learn more.

使用 gather 计算 tall 数组并将结果传入内存中。

[Qexact,Qapprox] = gather(Qexact,Qapprox);

Evaluating tall expression using the Local MATLAB Session:
- Pass 1 of 1: Completed in 2.4 sec
Evaluation completed in 3.3 sec

显示 A（沿第二个维度）在累积概率 0.25、0.5 和 0.75 下的精确分位数的前五行。

Qexact(1:5,:)

ans = 5×3
10³ ×

    0.0305    0.3475    0.6885
    0.0355    0.5420    1.0725
    0.0520    1.0690    2.1365
    0.0360    0.6955    1.3815
    0.0405    0.3530    0.6875

矩阵 Qexact 的每行都包含 A 中对应行的三个分位数。例如，30.5、347.5 和 688.5 分别是 A 中第一行的 0.25、0.5 和 0.75 分位数。

显示 A（沿第一个维度）在累积概率 0.25、0.5 和 0.75 下的近似分位数。

Qapprox

Qapprox = 3×4
10³ ×

   -0.0070    1.1149    0.9321    0.0700
         0    1.5220    1.3350    0.1020
    0.0110    1.9180    1.7400    0.1510

矩阵 Qapprox 的每列都包含 A 中对应列的三个分位数。例如，Qapprox 的第一列（元素为 -7、0 和 11）包含 A 的第一列的分位数。

tall 矩阵在 `n` 个等间距概率下的分位数

打开实时脚本

计算 tall 矩阵在给定数量的等间距累积概率下沿其不同维度的精确和近似分位数。

mapreducer(0)

varnames = ["ArrDelay","ArrTime","DepTime","ActualElapsedTime"];
ds = datastore("airlinesmall.csv","TreatAsMissing","NA", ...
    "SelectedVariableNames",varnames);
tt = tall(ds);
A = tt{:,varnames}

A =

  M×4 tall double matrix

           8         735         642          53
           8        1124        1021          63
          21        2218        2055          83
          13        1431        1332          59
           4         746         629          77
          59        1547        1446          61
           3        1052         928          84
          11        1134         859         155
          :          :            :           :
          :          :            :           :

要计算在等间距累积概率下沿第一个维度的分位数，您必须使用基于 T-Digest 的逼近算法。如果使用基于排序的算法（参阅算法）计算 tall 数组沿第一个维度的分位数，计算量会很大。

计算 A 在三个等间距累积概率下沿其第一个维度的分位数。由于默认维度是 1，因此无需为 dim 指定值。将 method 指定为 "approximate" 以使用逼近算法。

Qapprox = quantile(A,3,Method="approximate")

Qapprox =

  M×N×... tall array

    ?    ?    ?    ...
    ?    ?    ?    ...
    ?    ?    ?    ...
    :    :    :
    :    :    :

Preview deferred. Learn more.

要计算在等间距累积概率下沿任何其他维度（dim 不是 1）的分位数，quantile 仅计算精确分位数，以便它通过使用基于排序的算法高效执行计算。

计算 A 在三个等间距累积概率下沿第二个维度的分位数。由于 dim 不是 1，quantile 默认返回精确分位数。

Qexact = quantile(A,3,2)

Qexact =

  M×N×... tall array

    ?    ?    ?    ...
    ?    ?    ?    ...
    ?    ?    ?    ...
    :    :    :
    :    :    :

Preview deferred. Learn more.

使用 gather 计算 tall 数组并将结果传入内存中。

[Qapprox,Qexact] = gather(Qapprox,Qexact);

Evaluating tall expression using the Local MATLAB Session:
- Pass 1 of 1: Completed in 1.6 sec
Evaluation completed in 1.8 sec

显示 A 在三个等间距累积概率下沿第一个维度的近似分位数。

Qapprox

Qapprox = 3×4
10³ ×

   -0.0070    1.1149    0.9321    0.0700
         0    1.5220    1.3350    0.1020
    0.0110    1.9180    1.7400    0.1510

矩阵 Qapprox 的每列都包含 A 中对应列的分位数。例如，Qapprox 的第一列（元素为 -7、0 和 11）包含 A 的第一列的分位数。

显示 A 在三个等间距累积概率下沿第二个维度的精确分位数的前五行。

Qexact(1:5,:)

ans = 5×3
10³ ×

    0.0305    0.3475    0.6885
    0.0355    0.5420    1.0725
    0.0520    1.0690    2.1365
    0.0360    0.6955    1.3815
    0.0405    0.3530    0.6875

矩阵 Qexact 的每行都包含 A 中对应行的三个等间距分位数。例如，30.5、347.5 和 688.5 分别是 A 中第一行的 0.25、0.5 和 0.75 分位数。

输入参数

全部折叠

`A` — 输入数组
向量 | 矩阵 | 多维数组

输入数组，指定为向量、矩阵或多维数组。

数据类型: double | single | duration

`p` — 用于计算分位数的累积概率
标量 | 向量

用于计算分位数的累积概率，指定为从 0 到 1 的标量或标量向量。

示例: 0.3

示例: [0.25, 0.5, 0.75]

示例: (0:0.25:1)

数据类型: double | single

`n` — 用于计算分位数的概率的数量
正整数标量

用于计算分位数的概率的数量，指定为正整数标量。quantile 返回 n 个分位数，这些分位数将数据集分成均匀分布的 n+1 个区间。

数据类型: double | single

`dim` — 沿其运算的维度
正整数标量

沿其运算的维度，指定为正整数标量。如果不指定维度，则默认值是大小不等于 1 的第一个数组维度。

假设有一个输入矩阵 A 和一个由累积概率 p 组成的向量：

Q = quantile(A,p,1) 计算 A 中各列在累积概率 p 下的分位数。由于 1 是指定的运算维度，Q 有 length(p) 行。
Q = quantile(A,p,2) 计算 A 中各行在累积概率 p 下的分位数。由于 2 是指定的运算维度，Q 有 length(p) 列。

假设有一个输入矩阵 A 和一个由 n 个等间距概率组成的向量：

Q = quantile(A,n,1) 计算 A 中各列在 n 个等间距累积概率下的分位数。由于 1 是指定的运算维度，Q 有 n 行。
Q = quantile(A,n,2) 计算 A 中各行在 n 个等间距累积概率下的分位数。由于 2 是指定的运算维度，Q 有 n 列。

维度 dim 表示长度等于 length(p) 或 n 的 Q 的维度。

`vecdim` — 要沿其运算的维度组成的向量
正整数向量

要沿其运算的维度组成的向量，指定为正整数向量。每个元素代表输入数据的一个维度。

输出 Q 在最小指定运算维度中的大小等于 length(p) 或 n。Q 在 vecdim 中指定的其他运算维度中的大小为 1。Q 在 vecdim 中未指定的所有维度中的大小保持与输入数据相同。

假设有一个 2×3×3 输入数组 A 和累积概率 p。quantile(A,p,[1 2]) 将返回一个 length(p)×1×3 数组，因为 1 和 2 是运算维度且 min([1 2]) = 1。返回的数组的每页都包含 A 的对应页中元素的分位数。

`method` — 计算分位数的方法
`"midpoint"` (默认) | `"inclusive"` | `"exclusive"` | `"approximate"`

计算分位数的方法，指定为以下值之一：

"midpoint" - 通过使用排序的中点算法计算分位数。
在 R2025a 之前的版本中: 对此方法使用 "exact"。
"inclusive" - 通过使用排序的算法计算分位数，该算法将第 0 个和第 1 个分位数包含在数据边界内。 (自 R2025a 起)
"exclusive" - 通过使用排序的算法计算分位数，该算法将第 0 个和第 1 个分位数排除在数据边界外。 (自 R2025a 起)
"approximate" - 通过使用 T-Digest 的算法计算近似分位数（适用于 double 或 single 输入数组）。

有关分位数计算的详细信息，请参阅算法。

详细信息

全部折叠

线性插值

线性插值使用线性多项式求 y_i = f(x_i)，即底层函数 Y = f(X) 在向量或数组 x 中的点处的值。如有数据点 (x₁, y₁) 和 (x₂, y₂)，其中 y₁ = f(x₁) 且 y₂ = f(x₂)，则线性插值根据下式计算 y₁ 和 x₂ 之间给定 x 处的 x= f(x)：

$y = f (x) = y_{1} + \frac{(x - x_{1})}{(x_{2} - x_{1})} (y_{2} - y_{1}) .$

同样，如果 1.5/n 分位数是 y_1.5/n 并且 2.5/n 分位数是 y_2.5/n，则线性插值找到 2.3/n 分位数 y_2.3/n 为

$y_{\frac{2.3}{n}} = y_{\frac{1.5}{n}} + \frac{(\frac{2.3}{n} - \frac{1.5}{n})}{(\frac{2.5}{n} - \frac{1.5}{n})} (y_{\frac{2.5}{n}} - y_{\frac{1.5}{n}}) .$

T-Digest

T-digest [2] 是一种概率数据结构体，它是数据集的经验累积分布函数 (CDF) 的稀疏表示。T-digest 可用于根据在线或分布式数据计算基于秩的统计量（例如百分位数和分位数）的逼近值，所采用的方式支持可控精度，特别是在数据分布的尾部附近。

对于分布在不同分区中的数据，T-digest 会单独计算每个数据分区的分位数估计值（和百分位数估计值），然后合并这些估计值，同时保持恒定的内存界限和恒定的计算相对精度（对于第 q 个分位数，为 $q (1 - q)$ ）。由于这些原因，T-digest 在处理 tall 数组时非常实用。

要估计分布在不同分区中的数组的分位数，首先在数据的每个分区中构建一个 T-digest。T-digest 对分区中的数据进行聚类，并通过质心值和表示对聚类有贡献的样本数量的累积权重来汇总每个聚类。T-digest 使用大簇（质心间距大）表示 q = 0.5 附近的 CDF 区域，使用小簇（质心间距小）表示 q = 0 和 q = 1 附近的 CDF 区域。

T-digest 通过使用缩放函数控制簇大小，该函数使用压缩参数 δ 将分位数 q 映射到索引 k。即

$k (q, δ) = δ \cdot (\frac{\sin^{- 1} (2 q - 1)}{π} + \frac{1}{2}),$

，其中映射 k 呈单调形态，最小值为 k(0,δ) = 0，最大值为 k(1,δ) = δ。下图显示了 δ = 10 的缩放函数。

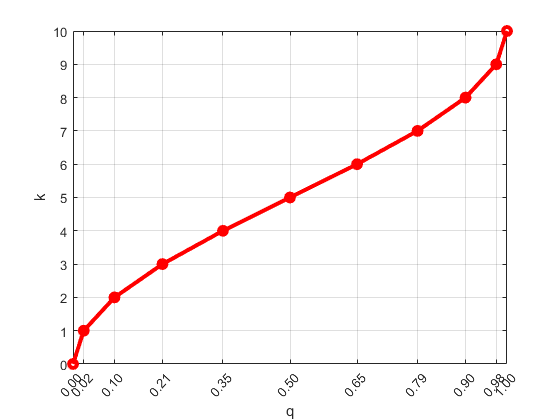
Scaling function plotted with q on the x-axis and k on the y-axis

缩放函数将分位数 q 转换为缩放因子 k，以便在 q 中给出可变大小的步。因此，簇大小不相等（中心分位数附近的簇较大，q = 0 和 q = 1 附近的簇较小）。较小的簇使得数据边缘附近的准确度更高。

要用具有权重和位置的新观测值更新 T-digest，请找到距离新观测值最近的簇。然后，添加权重，并基于加权平均值更新簇质心，前提是更新后的簇权重不超过大小限制。

您可以合并来自每个数据分区的独立 T-digest，方法是对这些 T-digest 求并集，并合并其质心。要合并 T-digest，请首先对来自所有独立 T-digest 的簇按簇权重降序排序。然后，合并满足大小限制的相邻簇，以形成一个新 T-digest。

一旦形成表示完整数据集的 T-digest，就可以估计 T-digest 中每个簇的端点（或边界），然后使用每个簇的端点之间的插值来计算准确的分位数估计值。

算法

对于 n 元素向量 A，当您选择除 "approximate" 之外的任何方法时，quantile 函数使用基于排序的算法计算分位数。

A 中的排序元素根据选定方法映射到分位数，如下表中所述。

分位数	`Method`
分位数	`"midpoint"` 在 R2025a 之前的版本中: `"exact"`	`"inclusive"` (自 R2025a 起)	`"exclusive"` (自 R2025a 起)
第一个排序元素的分位数	1/(2n)	0	1/(n+1)
第二个排序元素的分位数	3/(2n)	1/(n−1)	2/(n+1)
第三个排序元素的分位数	5/(2n)	2/(n−1)	3/(n+1)
...	...	...	...
第 k 个排序元素的分位数	(2k−1)/(2n)	(k−1)/(n−1)	k/(n+1)
...	...	...	...
第 (n−1) 个排序元素的分位数	(2n−3)/(2n)	(n−2)/(n−1)	(n−1)/(n+1)
第 n 个排序元素的分位数	(2n−1)/(2n)	1	n/(n+1)

例如，如果 A 是 [6 3 2 10 1]，则分位数如下表所示。

分位数	`Method`
分位数	`"midpoint"` 在 R2025a 之前的版本中: `"exact"`	`"inclusive"` (自 R2025a 起)	`"exclusive"` (自 R2025a 起)
`1` 的分位数	1/10	0	1/6
`2` 的分位数	3/10	1/4	1/3
`3` 的分位数	1/2	1/2	1/2
`6` 的分位数	7/10	3/4	2/3
`10` 的分位数	9/10	1	5/6

quantile 函数使用线性插值计算在 A 的第一个和最后一个排序元素的概率之间的概率下的分位数。有关详细信息，请参阅线性插值。
例如，如果 A 是 [6 3 2 10 1]，则：
- 对于中点方法，第 0.4 个分位数是 2.5。
  在 R2025a 之前的版本中: 对于精确方法，第 0.4 个分位数是 2.5。
- 对于包含方法，第 0.4 个分位数是 2.6。 (自 R2025a 起)
- 对于排除方法，第 0.4 个分位数是 2.4。 (自 R2025a 起)
quantile 函数将 A 中元素的最小值或最大值赋给该范围之外的概率对应的分位数。
例如，如果 A 是 [6 3 2 10 1]，则对于中点方法和排除方法，第 0.05 个分位数是 1。 (自 R2025a 起)
在 R2025a 之前的版本中: 例如，如果 A 是 [6 3 2 10 1]，则对于精确方法，第 0.05 个分位数是 1。

quantile 函数将 NaN 值视为缺失值并将其删除。

参考

[1] Langford, E. “Quartiles in Elementary Statistics”, Journal of Statistics Education. Vol. 14, No. 3, 2006.

[2] Dunning, T., and O. Ertl. “Computing Extremely Accurate Quantiles Using T-Digests.” August 2017.

扩展功能

全部展开

tall 数组
对行数太多而无法放入内存的数组进行计算。

quantile 函数支持 tall 数组，但存在以下使用说明和限制：

仅当 A 是 tall 数值列向量时，Q = quantile(A,p) 和 Q = quantile(A,n) 才返回精确分位数（使用基于排序的算法）。
仅当满足以下条件之一时，Q = quantile(__,dim) 才返回精确分位数：
- A 是 tall 数值列向量。
- A 是 tall 数值数组且 dim 不是 1。例如，quantile(A,p,2) 返回 tall 数组 A 沿行的精确分位数。
如果 A 是 tall 数组且 dim 是 1，则您必须将 method 指定为 "approximate"，以使用基于 T-Digest 的逼近算法计算分位数。例如，quantile(A,p,1,"Method","approximate") 返回 tall 数组 A 沿列的近似分位数。
仅当满足以下条件之一时，Q = quantile(__,vecdim) 才返回精确分位数：
- A 是 tall 数值列向量。
- A 是 tall 数值数组且 vecdim 不包含 1。例如，如果 A 是 3×5×2 数组，则 quantile(A,p,[2,3]) 返回每个 A(i,:,:) 切片中元素的精确分位数。
- A 是 tall 数值数组且 vecdim 包含 1 以及 A 中其大小不等于 1 的所有维度。例如，如果 A 是 10×1×4 数组，则 quantile(A,p,[1 3]) 返回 A(:,1,:) 中元素的精确分位数。
如果 A 是 tall 数值数组且 vecdim 包含 1 但不包含 A 中其大小不等于 1 的所有维度，则必须将 method 指定为 "approximate" 以使用逼近算法。例如，如果 A 是 10×1×4 数组，您可以使用 quantile(A,p,[1 2],"Method","approximate") 计算 A 的每页的近似分位数。

有关详细信息，请参阅 tall 数组。

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

不支持 "all" 和 vecdim 输入。
不支持 Method 名称-值参量。
dim 输入参量必须为编译时常量。
如果不指定 dim 输入参量，生成的代码中的工作（或运算）维度可能不同。因此，可能会发生运行时错误。有关详细信息，请参阅在默认维度选择方面与 MATLAB 不兼容 (MATLAB Coder)。
如果输出 Q 是向量，当以下所有条件都满足时，Q 的方向与 MATLAB^® 不同：
- 未提供 dim。
- A 在编译时是可变大小数组，而不是可变大小向量，但在运行时 A 是向量。
- 向量 A 的方向与向量 p 的方向不匹配。
在这种情况下，输出 Q 与 A 的方向匹配，而不是与 p 的方向匹配。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

quantile 函数支持 GPU 数组输入，但有以下用法说明和限制：

不支持 "all" 和 vecdim 输入。
不支持 Method 名称-值参量。

有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2006a 之前推出

全部展开

R2025a: 使用包含方法和排除方法计算分位数

您可以使用包含方法或排除方法计算分位数。将方法名称分别指定为 "inclusive" 或 "exclusive"。"inclusive" 方法在数据边界内包含第 0 个和第 1 个分位数；"exclusive" 方法则排除它们。

此外，默认方法的名称已从 "exact" 更改为 "midpoint"。quantile 函数继续支持 Method="exact" 以实现向后兼容。

以下示例说明默认方法与两种新方法之间的差异。

x = 1:5;
Q = quantile(x,1/4,Method="midpoint")

Q = 1.7500

x = 1:5;
Q = quantile(x,1/4,Method="inclusive")

Q = 2

x = 1:5;
Q = quantile(x,1/4,Method="exclusive")

Q = 1.5000

R2022a: 从 Statistics and Machine Learning Toolbox 移至 MATLAB

以前，quantile 需要 Statistics and Machine Learning Toolbox™。

另请参阅

prctile | median | iqr

quantile

语法

说明

示例

给定概率的分位数

n 个等间距累积概率对应的分位数

矩阵在给定概率下的分位数

矩阵在 n 个等间距概率下的分位数

多维数组在给定概率下的分位数

偶数个数据元素的中位数和四分位数

奇数个数据元素的中位数和四分位数

tall 向量在给定概率下的分位数

tall 矩阵沿不同维度的分位数

tall 矩阵在 n 个等间距概率下的分位数

输入参数

A — 输入数组 向量 | 矩阵 | 多维数组

p — 用于计算分位数的累积概率 标量 | 向量

n — 用于计算分位数的概率的数量 正整数标量

dim — 沿其运算的维度 正整数标量

vecdim — 要沿其运算的维度组成的向量 正整数向量

method — 计算分位数的方法 "midpoint" (默认) | "inclusive" | "exclusive" | "approximate"

详细信息

线性插值

T-Digest

算法

参考

扩展功能

tall 数组 对行数太多而无法放入内存的数组进行计算。

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

版本历史记录

R2025a: 使用包含方法和排除方法计算分位数

R2022a: 从 Statistics and Machine Learning Toolbox 移至 MATLAB

另请参阅

`n` 个等间距累积概率对应的分位数

矩阵在 `n` 个等间距概率下的分位数

tall 矩阵在 `n` 个等间距概率下的分位数

`A` — 输入数组
向量 | 矩阵 | 多维数组

`p` — 用于计算分位数的累积概率
标量 | 向量

`n` — 用于计算分位数的概率的数量
正整数标量

`dim` — 沿其运算的维度
正整数标量

`vecdim` — 要沿其运算的维度组成的向量
正整数向量

`method` — 计算分位数的方法
`"midpoint"` (默认) | `"inclusive"` | `"exclusive"` | `"approximate"`

tall 数组
对行数太多而无法放入内存的数组进行计算。

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。