median

数组的中位数值

全页折叠

语法

M = median(A)

M = median(A,"all")

M = median(A,dim)

M = median(A,vecdim)

M = median(___,missingflag)

M = median(___,Weights=W)

说明

M = median(A) 返回 A 的中位数值。

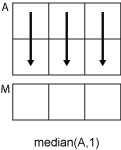
如果 A 为向量，则 median(A) 返回 A 的中位数值。
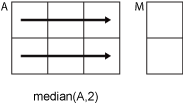
如果 A 为非空矩阵，则 median(A) 将 A 的各列视为向量，并返回中位数值的行向量。
如果 A 为 0×0 空矩阵，median(A) 返回 NaN。
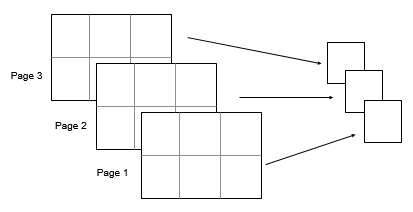
如果 A 是一个多维数组，则 median(A) 会将沿大小不等于 1 的第一个数组维度的值视为向量。此维度中 M 的大小变为 1，而所有其他维度的大小仍与在 A 中相同。
如果 A 是表或时间表，则 median(A) 返回包含每个变量的中位数的单行表。 (自 R2023a 起)

median 固有地以与 A 相同的类返回值，使得 class(M) = class(A)。

示例

M = median(A,"all") 返回 A 的所有元素的中位数。

示例

M = median(A,dim) 返回维度 dim 上元素的中位数。例如，如果 A 为矩阵，则 median(A,2) 返回包含每一行的中位数值的列向量。

示例

M = median(A,vecdim) 返回向量 vecdim 所指定的维度上的中位数。例如，如果 A 是矩阵，则 median(A,[1 2]) 返回 A 中所有元素的中位数，因为矩阵的每个元素包含在由维度 1 和 2 定义的数组切片中。

示例

M = median(___,missingflag) 在上述任一语法的基础上指定包含还是省略 A 中的缺失值。例如，median(A,"omitmissing") 在计算中位数时会忽略所有缺失值。默认情况下，median 包括缺失值。

示例

M = median(___,Weights=W) 指定加权方案 W 并返回加权中位数。 (自 R2024a 起)

示例

全部折叠

矩阵列的中位数

打开实时脚本

定义一个 4×3 矩阵。

A = [0 1 1; 2 3 2; 1 3 2; 4 2 2]

A = 4×3

     0     1     1
     2     3     2
     1     3     2
     4     2     2

计算每一列的中位数值。

M = median(A)

M = 1×3

    1.5000    2.5000    2.0000

对于每一列，中位数值在排列顺序上位于中间的两个数值的均值。

矩阵行的中位数

打开实时脚本

定义一个 2×3 矩阵。

A = [0 1 1; 2 3 2]

A = 2×3

     0     1     1
     2     3     2

计算每一行的中位数值。

M = median(A,2)

对于每一行，中位数值为在排列顺序上位于中间的数值。

三维数组的中位数

打开实时脚本

创建一个由 1 和 10 之间的整数组成的 1×3×4 数组。

rng('default')
A = randi(10,[1,3,4])

A = 
A(:,:,1) =

     9    10     2


A(:,:,2) =

    10     7     1


A(:,:,3) =

     3     6    10


A(:,:,4) =

    10     2    10

沿第二个维度计算此三维数组的中位数值。

M = median(A)

M = 
M(:,:,1) =

     9


M(:,:,2) =

     7


M(:,:,3) =

     6


M(:,:,4) =

    10

此运算通过沿第二个维度计算三个值的中位数来生成一个 1×1×4 数组。第二个维度的大小降到 1。

沿 A 的第一个维度计算中位数。

M = median(A,1);
isequal(A,M)

ans = logical
   1

此命令会返回与 A 相同的数组，因为第一个维度的大小为 1。

数组页的中位数

打开实时脚本

创建一个三维数组并计算每页数据（行和列）的中位数。

A(:,:,1) = [2 4; -2 1];
A(:,:,2) = [6 2; -5 3];
A(:,:,3) = [4 4; 7 -3];
M1 = median(A,[1 2])

M1 = 
M1(:,:,1) =

    1.5000


M1(:,:,2) =

    2.5000


M1(:,:,3) =

     4

要计算一个数组的所有维度上的中位数，可以在向量维参量中指定每个维度，或使用 "all" 选项。

M2 = median(A,[1 2 3])

M2 = 
2.5000

Mall = median(A,"all")

Mall = 
2.5000

8 位整数数组的中位数

打开实时脚本

定义一个由 8 位整数组成的 1×4 向量。

A = int8(1:4)

A = 1×4 int8 row vector

   1   2   3   4

计算中位数值。

M = median(A)

M = int8

3

class(M)

ans = 
'int8'

M 为在排列顺序上位于中间的两个数值的均值（以一个 8 位整数返回）。

排除缺失值的中位数

打开实时脚本

创建一个包含 NaN 值的矩阵。

A = [1.77 -0.005 NaN -2.95; NaN 0.34 NaN 0.19]

A = 2×4

    1.7700   -0.0050       NaN   -2.9500
       NaN    0.3400       NaN    0.1900

计算矩阵的中位数值，不包括缺失值。对于包含任一 NaN 值的矩阵列，中位数是在非 NaN 元素上计算的。对于包含的值都是 NaN 的矩阵列，中位数为 NaN。

M = median(A,"omitmissing")

M = 1×4

    1.7700    0.1675       NaN   -1.3800

指定加权方案

自 R2024a 起

打开实时脚本

创建一个矩阵，并根据 W 指定的加权方案计算矩阵的加权中位数。median 函数将加权方案应用于 A 中的每列。

A = [1 1; 7 9; 1 9; 1 9; 6 2];
W = [1 2 1 2 3]';
M = median(A,Weights=W)

M = 1×2

     6     9

对于每一列，中位数值在排列顺序上位于中间的两个数值的均值。

输入参数

全部折叠

`A` — 输入数据
向量 | 矩阵 | 多维数组 | 表 | 时间表

输入数据，指定为向量、矩阵、多维数组、表或时间表。

`dim` — 沿其运算的维度
正整数标量

沿其运算的维度，指定为正整数标量。如果不指定维度，则默认值是大小不等于 1 的第一个数组维度。

维度 dim 表示长度减至 1 的维度。size(M,dim) 为 1，而所有其他维度的大小保持不变。

以一个 m×n 输入矩阵 A 为例：

median(A,1) 计算 A 的每列中元素的中位数，并返回一个 1×n 行向量。
median(A,2) 计算 A 的每行中元素的中位数，并返回一个 m×1 列向量。

当 dim 大于 ndims(A) 时，median 返回 A。

`vecdim` — 维度向量
正整数向量

维度向量，指定为正整数向量。每个元素代表输入数组的一个维度。指定的操作维度的输出长度为 1，而其他保持不变。

以 2×3×3 输入数组 A 为例。然后 median(A,[1 2]) 返回一个 1×1×3 数组，其元素是 A 的每个页面的中位数。

Mapping of a 2-by-3-by-3 input array to a 1-by-1-by-3 output array

`missingflag` — 缺失值条件
`"includemissing"` (默认) | `"includenan"` | `"includenat"` | `"includeundefined"` | `"omitmissing"` | `"omitnan"` | `"omitnat"` | `"omitundefined"`

缺失值条件，指定为下表中的值之一。

值	输入数据类型	描述
`"includemissing"`	所有支持的数据类型	在计算中位数时包括 `A` 中的缺失值。如果运算维度中的任一元素缺失，则 `M` 中的对应元素也会缺失。
`"includenan"`	`double`, `single`, `duration`
`"includenat"`	`datetime`
`"includeundefined"`	`categorical`
`"omitmissing"`	所有支持的数据类型	忽略 `A` 中的缺失值并基于较少的点计算中位数。如果运算维度中的所有元素都缺失，则 `M` 中的对应元素也会缺失。
`"omitnan"`	`double`, `single`, `duration`
`"omitnat"`	`datetime`
`"omitundefined"`	`categorical`

`W` — 加权方案
向量 | 矩阵 | 多维数组

自 R2024a 起

加权方案，指定为向量、矩阵或多维数组。W 的元素必须是非负值。

如果您指定一个加权方案，median 将返回加权中位数，即 A 中与 W [1] 指定的权重的累积 50% 相关联的值。与标准中位数相比，加权中位数受极值的影响较小。

如果 W 是向量，其长度必须与运算维度的长度相同。否则，W 的大小必须与输入数据的大小相同。

如果输入数据 A 是表或时间表，则 W 必须为向量。

如果指定 vecdim 或 "all"，则无法指定此参量。

数据类型: double | single

算法

对于有序分类数组，MATLAB^® 根据以下方式解释偶数个元素的中位数：

如果中间两个值之间的类别数为...	则中位数为 ...
零（值来自连续类别）	两个中间值中的较大者
奇数	位于两个中间值中间的类别的值
偶数	位于两个中间值中间的两个类别中较大者的值

参考

[1] “Weighted median.” In Wikipedia, May 21 2023. https://en.wikipedia.org/wiki/Weighted_median.

扩展功能

全部展开

tall 数组
对行数太多而无法放入内存的数组进行计算。

median 函数支持 tall 数组，但存在以下使用说明和限制：

输入 A 必须是列向量，才能计算第一个维度的 median。
不支持 Weights 名称-值参量。

有关详细信息，请参阅tall 数组。

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

如果使用参量 dim 和 vecdim，它们在代码生成时必须为常量。
对于输入参量 A：
- 如果不指定维度，代码生成器将沿输入数组中具有可变大小或其大小不为 1 的第一个维度进行运算。如果此维度在代码生成时具有可变大小且在运行时为 1，则可能发生运行时错误。为避免此错误，请指定维度。
- 如果输入数组的所有维度在代码生成时都具有可变大小，则此数组在运行时不能为空。
- 在生成的代码中，输入数组保持复数，即使其所有元素都具有零值虚部也是如此。在这些情况下，生成的代码产生的结果可能与 MATLAB 产生的结果不同。请参阅具有零值虚部的复数数据的代码生成 (MATLAB Coder)。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

用法说明和限制：

请参考“C/C++ 代码生成”一节中的用法说明和限制。同样的限制也适用于 GPU 代码生成。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

median 函数完全支持 GPU 数组。要在 GPU 上运行该函数，请将输入数据指定为 gpuArray (Parallel Computing Toolbox)。有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

此函数完全支持分布式数组。有关详细信息，请参阅使用分布式数组运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2006a 之前推出

全部展开

R2025a: 改进了 GPU 代码生成支持

GPU Coder™ 现在为 median 生成更优化的 CUDA^® 代码。必须具有 MATLAB Coder™ 和 GPU Coder 才能生成 CUDA 代码。

R2024b: 计算 `datetime` 和有序分类数据类型的加权中位数

您可以计算具有 datetime 和有序分类数据类型的输入数据的加权中位数。在 R2024b 之前，只能计算这些数据类型的未加权中位数。

R2024b: 改进了计算加权中位数时的性能

median 函数在您指定加权方案时表现出了更好的性能。

例如，以下代码计算一个 600×10 矩阵的加权中位数。代码的执行速度比上一版本大约快 1.8 倍。

function timingTest
A = rand(600,10);
W = rand(600,1);

for i = 1:1:3e2
    median(A,Weights=W); 
end
end

大致的执行时间是：

R2024a：1.00 秒

R2024b：0.55 秒

此代码是在运行 Windows^® 11 的 AMD EPYC 74F3 24 核处理器 @ 3.19 GHz 测试系统上使用 timeit 函数计时的。

timeit(@timingTest)

R2024a: 计算加权中位数

通过将 Weights 参数指定为加权方案来计算加权中位数。您可以计算具有数值、逻辑值和 duration 数据类型的输入数据的加权中位数。

R2023a: 指定缺失值条件

使用 "includemissing" 或 "omitmissing" 选项计算中位数时，包括还是忽略输入数组中的所有缺失值。以前，"includenan"、"omitnan"、"includenat"、"omitnat"、"includeundefined" 和 "omitundefined" 指定特定于输入数组的数据类型的缺失值条件。

R2023a: 直接对表和时间表执行计算

median 函数可以对表或时间表中的所有变量执行计算，而无需通过索引访问这些变量。所有变量都必须具有支持计算的数据类型。有关详细信息，请参阅Direct Calculations on Tables and Timetables。

R2018b: 对多个维度执行运算

一次对输入数组的多个维度执行运算。指定一个由运算维度组成的向量，或指定 "all" 选项以对所有数组维度执行运算。

另请参阅

corrcoef | cov | max | mean | min | mode | std | var

median

语法

说明

示例

矩阵列的中位数

矩阵行的中位数

三维数组的中位数

数组页的中位数

8 位整数数组的中位数

排除缺失值的中位数

指定加权方案

输入参数

A — 输入数据 向量 | 矩阵 | 多维数组 | 表 | 时间表

dim — 沿其运算的维度 正整数标量

vecdim — 维度向量 正整数向量

missingflag — 缺失值条件 "includemissing" (默认) | "includenan" | "includenat" | "includeundefined" | "omitmissing" | "omitnan" | "omitnat" | "omitundefined"

W — 加权方案 向量 | 矩阵 | 多维数组

算法

参考

扩展功能

tall 数组 对行数太多而无法放入内存的数组进行计算。

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成 使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组 使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

版本历史记录

R2025a: 改进了 GPU 代码生成支持

R2024b: 计算 datetime 和有序分类数据类型的加权中位数

R2024b: 改进了计算加权中位数时的性能

R2024a: 计算加权中位数

R2023a: 指定缺失值条件

R2023a: 直接对表和时间表执行计算

R2018b: 对多个维度执行运算

另请参阅

`A` — 输入数据
向量 | 矩阵 | 多维数组 | 表 | 时间表

`dim` — 沿其运算的维度
正整数标量

`vecdim` — 维度向量
正整数向量

`missingflag` — 缺失值条件
`"includemissing"` (默认) | `"includenan"` | `"includenat"` | `"includeundefined"` | `"omitmissing"` | `"omitnan"` | `"omitnat"` | `"omitundefined"`

`W` — 加权方案
向量 | 矩阵 | 多维数组

tall 数组
对行数太多而无法放入内存的数组进行计算。

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

R2024b: 计算 `datetime` 和有序分类数据类型的加权中位数