fscmrmr
Rank features for classification using minimum redundancy maximum relevance (MRMR) algorithm
Syntax
Description
fscmrmr ranks features (predictors) using the MRMR algorithm to
identify important predictors for classification problems.
To perform MRMR-based feature ranking for regression, see fsrmrmr.
idx = fscmrmr(Tbl,ResponseVarName)idx, ordered by predictor importance
(from most important to least important). The table Tbl contains the
predictor variables and a response variable, ResponseVarName, which
contains the class labels. You can use idx to select important
predictors for classification problems.
idx = fscmrmr(___,Name,Value)
Examples
Load the sample data.
load ionosphereRank the predictors based on importance.
[idx,scores] = fscmrmr(X,Y);
Create a bar plot of the predictor importance scores.
bar(scores(idx)) xlabel('Predictor rank') ylabel('Predictor importance score')

The drop in score between the first and second most important predictors is large, while the drops after the sixth predictor are relatively small. A drop in the importance score represents the confidence of feature selection. Therefore, the large drop implies that the software is confident of selecting the most important predictor. The small drops indicate that the difference in predictor importance are not significant.
Select the top five most important predictors. Find the columns of these predictors in X.
idx(1:5)
ans = 1×5
5 4 1 7 24
The fifth column of X is the most important predictor of Y.
Find important predictors by using fscmrmr. Then compare the accuracies of the full classification model (which uses all the predictors) and a reduced model that uses the five most important predictors by using testckfold.
Load the census1994 data set.
load census1994The table adultdata in census1994 contains demographic data from the US Census Bureau to predict whether an individual makes over $50,000 per year. Display the first three rows of the table.
head(adultdata,3)
age workClass fnlwgt education education_num marital_status occupation relationship race sex capital_gain capital_loss hours_per_week native_country salary
___ ________________ __________ _________ _____________ __________________ _________________ _____________ _____ ____ ____________ ____________ ______________ ______________ ______
39 State-gov 77516 Bachelors 13 Never-married Adm-clerical Not-in-family White Male 2174 0 40 United-States <=50K
50 Self-emp-not-inc 83311 Bachelors 13 Married-civ-spouse Exec-managerial Husband White Male 0 0 13 United-States <=50K
38 Private 2.1565e+05 HS-grad 9 Divorced Handlers-cleaners Not-in-family White Male 0 0 40 United-States <=50K
The output arguments of fscmrmr include only the variables ranked by the function. Before passing a table to the function, move the variables that you do not want to rank, including the response variable and weight, to the end of the table so that the order of the output arguments is consistent with the order of the table.
In the table adultdata, the third column fnlwgt is the weight of the samples, and the last column salary is the response variable. Move fnlwgt to the left of salary by using the movevars function.
adultdata = movevars(adultdata,'fnlwgt','before','salary'); head(adultdata,3)
age workClass education education_num marital_status occupation relationship race sex capital_gain capital_loss hours_per_week native_country fnlwgt salary
___ ________________ _________ _____________ __________________ _________________ _____________ _____ ____ ____________ ____________ ______________ ______________ __________ ______
39 State-gov Bachelors 13 Never-married Adm-clerical Not-in-family White Male 2174 0 40 United-States 77516 <=50K
50 Self-emp-not-inc Bachelors 13 Married-civ-spouse Exec-managerial Husband White Male 0 0 13 United-States 83311 <=50K
38 Private HS-grad 9 Divorced Handlers-cleaners Not-in-family White Male 0 0 40 United-States 2.1565e+05 <=50K
Rank the predictors in adultdata. Specify the column salary as the response variable.
[idx,scores] = fscmrmr(adultdata,'salary','Weights','fnlwgt');
Create a bar plot of predictor importance scores. Use the predictor names for the x-axis tick labels.
bar(scores(idx)) xlabel('Predictor rank') ylabel('Predictor importance score') xticklabels(strrep(adultdata.Properties.VariableNames(idx),'_','\_')) xtickangle(45)
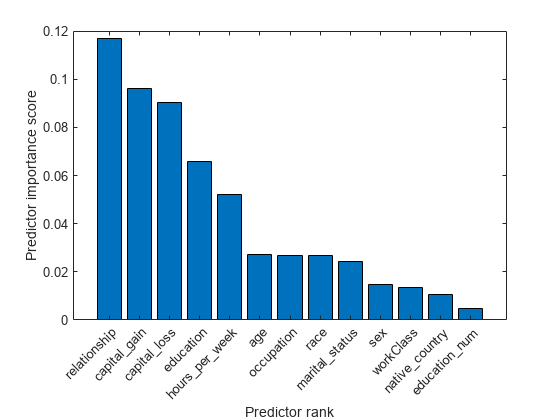
The five most important predictors are relationship, capital_loss, capital_gain, education, and hours_per_week.
Compare the accuracy of a classification tree trained with all predictors to the accuracy of one trained with the five most important predictors.
Create a classification tree template using the default options.
C = templateTree;
Define the table tbl1 to contain all predictors and the table tbl2 to contain the five most important predictors.
tbl1 = adultdata(:,adultdata.Properties.VariableNames(idx(1:13))); tbl2 = adultdata(:,adultdata.Properties.VariableNames(idx(1:5)));
Pass the classification tree template and the two tables to the testckfold function. The function compares the accuracies of the two models by repeated cross-validation. Specify 'Alternative','greater' to test the null hypothesis that the model with all predictors is, at most, as accurate as the model with the five predictors. The 'greater' option is available when 'Test' is '5x2t' (5-by-2 paired t test) or '10x10t' (10-by-10 repeated cross-validation t test).
[h,p] = testckfold(C,C,tbl1,tbl2,adultdata.salary,'Weights',adultdata.fnlwgt,'Alternative','greater','Test','5x2t')
h = logical
0
p = 0.9970
h equals 0 and the p-value is almost 1, indicating failure to reject the null hypothesis. Using the model with the five predictors does not result in loss of accuracy compared to the model with all the predictors.
Now train a classification tree using the selected predictors.
mdl = fitctree(adultdata,'salary ~ relationship + capital_loss + capital_gain + education + hours_per_week', ... 'Weights',adultdata.fnlwgt)
mdl =
ClassificationTree
PredictorNames: {'education' 'relationship' 'capital_gain' 'capital_loss' 'hours_per_week'}
ResponseName: 'salary'
CategoricalPredictors: [1 2]
ClassNames: [<=50K >50K]
ScoreTransform: 'none'
NumObservations: 32561
Properties, Methods
Input Arguments
Sample data, specified as a table. Multicolumn variables and cell arrays other than cell arrays of character vectors are not allowed.
Each row of Tbl corresponds to one observation, and each column corresponds
to one predictor variable. Optionally, Tbl can contain additional
columns for a response variable and observation weights.
A response variable can be a categorical, character, or string array, logical or numeric vector, or cell array of character vectors. If the response variable is a character array, then each element of the response variable must correspond to one row of the array.
If
Tblcontains the response variable, and you want to use all remaining variables inTblas predictors, then specify the response variable by usingResponseVarName. IfTblalso contains the observation weights, then you can specify the weights by usingWeights.If
Tblcontains the response variable, and you want to use only a subset of the remaining variables inTblas predictors, then specify the subset of variables by usingformula.If
Tbldoes not contain the response variable, then specify a response variable by usingY. The response variable andTblmust have the same number of rows.
If fscmrmr uses a subset of variables in Tbl as
predictors, then the function indexes the predictors using only the subset. The values
in the 'CategoricalPredictors' name-value pair argument and the
output argument idx do not count the predictors that the function
does not rank.
fscmrmr considers NaN, ''
(empty character vector), "" (empty string),
<missing>, and <undefined> values
in Tbl for a response variable to be missing values.
fscmrmr does not use observations with missing values for a
response variable.
Data Types: table
Response variable name, specified as a character vector or string scalar containing the name of a variable in Tbl.
For example, if a response variable is the column Y of
Tbl (Tbl.Y), then specify
ResponseVarName as "Y".
Data Types: char | string
Explanatory model of the response variable and a subset of the predictor variables, specified
as a character vector or string scalar in the form "Y ~ x1 + x2 +
x3". In this form, Y represents the response variable, and
x1, x2, and x3 represent
the predictor variables.
To specify a subset of variables in Tbl as predictors, use a formula. If
you specify a formula, then fscmrmr does not rank any variables
in Tbl that do not appear in formula.
The variable names in the formula must be both variable names in
Tbl (Tbl.Properties.VariableNames) and valid
MATLAB® identifiers. You can verify the variable names in Tbl
by using the isvarname function. If the variable
names are not valid, then you can convert them by using the matlab.lang.makeValidName function.
Data Types: char | string
Response variable, specified as a numeric, categorical, or logical vector, a character or
string array, or a cell array of character vectors. Each row of Y
represents the labels of the corresponding row of X.
fscmrmr considers NaN, ''
(empty character vector), "" (empty string),
<missing>, and <undefined> values
in Y to be missing values. fscmrmr does
not use observations with missing values for Y.
Data Types: single | double | categorical | logical | char | string | cell
Predictor data, specified as a numeric matrix. Each row of X corresponds to one observation, and each column corresponds to one predictor variable.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'CategoricalPredictors',[1 2],'Verbose',2 specifies the first
two predictor variables as categorical variables and specifies the verbosity level as
2.
List of categorical predictors, specified as one of the values in this table.
| Value | Description |
|---|---|
| Vector of positive integers |
Each entry in the vector is an index value indicating that the corresponding predictor is
categorical. The index values are between 1 and If |
| Logical vector |
A |
| Character matrix | Each row of the matrix is the name of a predictor variable. The
names must match the names in Tbl. Pad the
names with extra blanks so each row of the character matrix has the
same length. |
| String array or cell array of character vectors | Each element in the array is the name of a predictor variable.
The names must match the names in Tbl. |
"all" | All predictors are categorical. |
By default, if the predictor data is a table
(Tbl), fscmrmr assumes that a variable is
categorical if it is a logical vector, unordered categorical vector, character array, string
array, or cell array of character vectors. If the predictor data is a matrix
(X), fscmrmr assumes that all predictors are
continuous. To identify any other predictors as categorical predictors, specify them by using
the CategoricalPredictors name-value argument.
Example: "CategoricalPredictors","all"
Example: CategoricalPredictors=[1 5 6 8]
Data Types: single | double | logical | char | string | cell
Names of the classes to use for ranking, specified as the comma-separated pair consisting of 'ClassNames' and a categorical, character, or string array, a logical or numeric vector, or a cell array of character vectors. ClassNames must have the same data type as Y or the response variable in Tbl.
If ClassNames is a character array, then each element must correspond to
one row of the array.
Use 'ClassNames' to:
Specify the order of the
Priordimensions that corresponds to the class order.Select a subset of classes for ranking. For example, suppose that the set of all distinct class names in
Yis{'a','b','c'}. To rank predictors using observations from classes'a'and'c'only, specify'ClassNames',{'a','c'}.
The default value for 'ClassNames' is the set of all distinct class names in Y or the response variable in Tbl. The default 'ClassNames' value has mathematical ordering if the response variable is ordinal. Otherwise, the default value has alphabetical ordering.
Example: 'ClassNames',{'b','g'}
Data Types: categorical | char | string | logical | single | double | cell
Prior probabilities for each class, specified as one of the following:
Character vector or string scalar.
Vector (one scalar value for each class). To specify the class order for the corresponding elements of
'Prior', set the'ClassNames'name-value argument.Structure
Swith two fields.S.ClassNamescontains the class names as a variable of the same type as the response variable inYorTbl.S.ClassProbscontains a vector of corresponding probabilities.
fscmrmr normalizes the weights in each class
('Weights') to add up to the value of the prior probability of
the respective class.
Example: 'Prior','uniform'
Data Types: char | string | single | double | struct
Indicator for whether to use missing values in predictors, specified as either
true to use the values for ranking, or false
to discard the values.
fscmrmr considers NaN,
'' (empty character vector), "" (empty
string), <missing>, and <undefined>
values to be missing values.
If you specify UseMissing as true, then
fscmrmr uses missing values for ranking. For a categorical
variable, fscmrmr treats missing values as an extra category.
For a continuous variable, fscmrmr places
NaN values in a separate bin for binning.
If you specify UseMissing as false, then
fscmrmr does not use missing values for ranking. Because
fscmrmr computes mutual information for each pair of
variables, the function does not discard an entire row when values in the row are
partially missing. fscmrmr uses all pair values that do not
include missing values.
Example: "UseMissing",true
Example: UseMissing=true
Data Types: logical
Verbosity level, specified as the comma-separated pair consisting of
'Verbose' and a nonnegative integer. The value of
Verbose controls the amount of diagnostic information that the
software displays in the Command Window.
0 —
fscmrmrdoes not display any diagnostic information.1 —
fscmrmrdisplays the elapsed times for computing Mutual Information and ranking predictors.≥ 2 —
fscmrmrdisplays the elapsed times and more messages related to computing mutual information. The amount of information increases as you increase the'Verbose'value.
Example: 'Verbose',1
Data Types: single | double
Observation weights, specified as the comma-separated pair consisting of
'Weights' and a vector of scalar values or the name of a variable
in Tbl. The function weights the observations in each row of
X or Tbl with the corresponding value in
Weights. The size of Weights must equal the
number of rows in X or Tbl.
If you specify the input data as a table Tbl, then
Weights can be the name of a variable in Tbl
that contains a numeric vector. In this case, you must specify
Weights as a character vector or string scalar. For example, if
the weight vector is the column W of Tbl
(Tbl.W), then specify 'Weights,'W'.
fscmrmr normalizes the weights in each class to add up to the value
of the prior probability of the respective class. Inf weights are not supported.
Data Types: single | double | char | string
Output Arguments
Indices of predictors in X or Tbl ordered by
predictor importance, returned as a 1-by-r numeric vector, where
r is the number of ranked predictors.
If Tbl contains the response variable, then the function indexes
the predictors excluding the response variable. For example, suppose
Tbl includes 10 columns and you specify the second column of
Tbl as the response variable. If idx(3) is
5, then the third most important predictor is the sixth column of
Tbl.
If fscmrmr uses a subset of variables in Tbl as
predictors, then the function indexes the predictors using only the subset. For example,
suppose Tbl includes 10 columns and you specify the last five
columns of Tbl as the predictor variables by using
formula. If idx(3) is 5,
then the third most important predictor is the 10th column in Tbl,
which is the fifth predictor in the subset.
Predictor scores, returned as a 1-by-r numeric vector, where r is the number of ranked predictors.
A large score value indicates that the corresponding predictor is important. Also, a drop in the feature importance score represents the confidence of feature selection. For example, if the software is confident of selecting a feature x, then the score value of the next most important feature is much smaller than the score value of x.
For example, suppose Tbl includes 10 columns and you specify the last five columns of Tbl as the predictor variables by using formula. Then, score(3) contains the score value of the 8th column in Tbl, which is the third predictor in the subset.
More About
The mutual information between two variables measures how much uncertainty of one variable can be reduced by knowing the other variable.
The mutual information I of the discrete random variables X and Z is defined as
If X and Z are independent, then I equals 0. If X and Z are the same random variable, then I equals the entropy of X.
The fscmrmr function uses this definition to compute the mutual
information values for both categorical (discrete) and continuous variables.
fscmrmr discretizes a continuous variable into 256 bins or the number
of unique values in the variable if it is less than 256. The function finds optimal
bivariate bins for each pair of variables using the adaptive algorithm [2].
Algorithms
The MRMR algorithm [1] finds an optimal set of features that is mutually and maximally dissimilar and can represent the response variable effectively. The algorithm minimizes the redundancy of a feature set and maximizes the relevance of a feature set to the response variable. The algorithm quantifies the redundancy and relevance using the mutual information of variables—pairwise mutual information of features and mutual information of a feature and the response. You can use this algorithm for classification problems.
The goal of the MRMR algorithm is to find an optimal set S of features that maximizes VS, the relevance of S with respect to a response variable y, and minimizes WS, the redundancy of S, where VS and WS are defined with mutual information I:
|S| is the number of features in S.
Finding an optimal set S requires considering all 2|Ω| combinations, where Ω is the entire feature set. Instead, the MRMR algorithm ranks features through the forward addition scheme, which requires O(|Ω|·|S|) computations, by using the mutual information quotient (MIQ) value.
where Vx and Wx are the relevance and redundancy of a feature, respectively:
The fscmrmr function ranks all features in Ω and
returns idx (the indices of features ordered by feature importance)
using the MRMR algorithm. Therefore, the computation cost becomes O(|Ω|2). The function quantifies the importance of a feature using a heuristic
algorithm and returns a score (scores). A large score value indicates
that the corresponding predictor is important. Also, a drop in the feature importance score
represents the confidence of feature selection. For example, if the software is confident of
selecting a feature x, then the score value of the next most important
feature is much smaller than the score value of x. You can use the
outputs to find an optimal set S for a given number of features.
fscmrmr ranks features as follows:
Select the feature with the largest relevance, . Add the selected feature to an empty set S.
Find the features with nonzero relevance and zero redundancy in the complement of S, Sc.
If Sc does not include a feature with nonzero relevance and zero redundancy, go to step 4.
Otherwise, select the feature with the largest relevance, . Add the selected feature to the set S.
Repeat Step 2 until the redundancy is not zero for all features in Sc.
Select the feature that has the largest MIQ value with nonzero relevance and nonzero redundancy in Sc, and add the selected feature to the set S.
Repeat Step 4 until the relevance is zero for all features in Sc.
Add the features with zero relevance to S in random order.
The software can skip any step if it cannot find a feature that satisfies the conditions described in the step.
References
[1] Ding, C., and H. Peng. "Minimum redundancy feature selection from microarray gene expression data." Journal of Bioinformatics and Computational Biology. Vol. 3, Number 2, 2005, pp. 185–205.
[2] Darbellay, G. A., and I. Vajda. "Estimation of the information by an adaptive partitioning of the observation space." IEEE Transactions on Information Theory. Vol. 45, Number 4, 1999, pp. 1315–1321.
Version History
Introduced in R2019bStarting in R2020a, you can specify whether to use or discard missing values in
predictors for ranking by using the 'UseMissing' name-value pair
argument. The default value of 'UseMissing' is false
because most classification training functions in Statistics and Machine Learning Toolbox™ do not use missing values for training.
In R2019b, fscmrmr used missing values in predictors by default. To
update your code, specify 'UseMissing',true.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)