fsulaplacian

Rank features for unsupervised learning using Laplacian scores

Syntax

idx = fsulaplacian(X)

idx = fsulaplacian(X,Name,Value)

[idx,scores] = fsulaplacian(___)

Description

idx = fsulaplacian(X) ranks features (variables) in X using the Laplacian scores. The function returns idx, which contains the indices of features ordered by feature importance. You can use idx to select important features for unsupervised learning.

example

idx = fsulaplacian(X,Name,Value) specifies additional options using one or more name-value pair arguments. For example, you can specify 'NumNeighbors',10 to create a similarity graph using 10 nearest neighbors.

example

[idx,scores] = fsulaplacian(___) also returns the feature scores scores, using any of the input argument combinations in the previous syntaxes. A large score value indicates that the corresponding feature is important.

Examples

collapse all

Rank Features by Importance

Open Live Script

Load the sample data.

load ionosphere

Rank the features based on importance.

[idx,scores] = fsulaplacian(X);

Create a bar plot of the feature importance scores.

bar(scores(idx))
xlabel('Feature rank')
ylabel('Feature importance score')

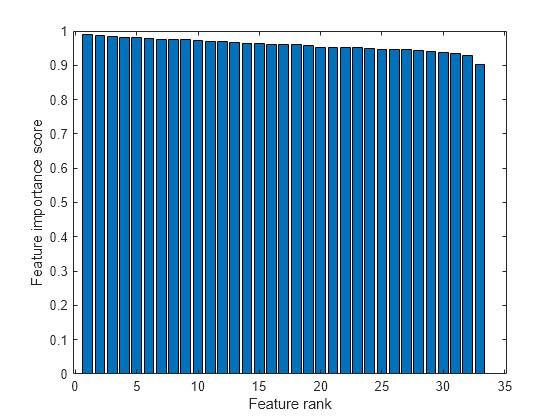
Figure contains an axes object. The axes object with xlabel Feature rank, ylabel Feature importance score contains an object of type bar.

Select the top five most important features. Find the columns of these features in X.

idx(1:5)

ans = 1×5

    15    13    17    21    19

The 15th column of X is the most important feature.

Rank Features Using Specified Similarity Matrix

Open Live Script

Compute a similarity matrix from Fisher's iris data set and rank the features using the similarity matrix.

Load Fisher's iris data set.

load fisheriris

Find the distance between each pair of observations in meas by using the pdist and squareform functions with the default Euclidean distance metric.

D = pdist(meas);
Z = squareform(D);

Construct the similarity matrix and confirm that it is symmetric.

S = exp(-Z.^2);
issymmetric(S)

ans = logical
   1

Rank the features.

idx = fsulaplacian(meas,'Similarity',S)

idx = 1×4

     3     4     1     2

Ranking using the similarity matrix S is the same as ranking by specifying 'NumNeighbors' as size(meas,1).

idx2 = fsulaplacian(meas,'NumNeighbors',size(meas,1))

idx2 = 1×4

     3     4     1     2

Input Arguments

collapse all

`X` — Input data
numeric matrix

Input data, specified as an n-by-p numeric matrix. The rows of X correspond to observations (or points), and the columns correspond to features.

The software treats NaNs in X as missing data and ignores any row of X containing at least one NaN.

Data Types: single | double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'NumNeighbors',10,'KernelScale','auto' specifies the number of nearest neighbors as 10 and the kernel scale factor as 'auto'.

`Similarity` — Similarity matrix
`[]` (empty matrix) (default) | symmetric matrix

Similarity matrix, specified as the comma-separated pair consisting of 'Similarity' and an n-by-n symmetric matrix, where n is the number of observations. The similarity matrix (or adjacency matrix) represents the input data by modeling local neighborhood relationships among the data points. The values in a similarity matrix represent the edges (or connections) between nodes (data points) that are connected in a similarity graph. For more information, see Similarity Matrix.

If you specify the 'Similarity' value, then you cannot specify any other name-value pair argument. If you do not specify the 'Similarity' value, then the software computes a similarity matrix using the options specified by the other name-value pair arguments.

Data Types: single | double

`Distance` — Distance metric
character vector | string scalar | function handle

Distance metric, specified as the comma-separated pair consisting of 'Distance' and a character vector, string scalar, or function handle, as described in this table.

Value	Description
`'euclidean'`	Euclidean distance (default)
`'seuclidean'`	Standardized Euclidean distance. Each coordinate difference between observations is scaled by dividing by the corresponding element of the standard deviation computed from `X`. Use the `Scale` name-value pair argument to specify a different scaling factor.
`'mahalanobis'`	Mahalanobis distance using the sample covariance of `X`, `C = cov(X,'omitrows')`. Use the `Cov` name-value pair argument to specify a different covariance matrix.
`'cityblock'`	City block distance
`'minkowski'`	Minkowski distance. The default exponent is 2. Use the `P` name-value pair argument to specify a different exponent, where `P` is a positive scalar value.
`'chebychev'`	Chebychev distance (maximum coordinate difference)
`'cosine'`	One minus the cosine of the included angle between observations (treated as vectors)
`'correlation'`	One minus the sample correlation between observations (treated as sequences of values)
`'hamming'`	Hamming distance, which is the percentage of coordinates that differ
`'jaccard'`	One minus the Jaccard coefficient, which is the percentage of nonzero coordinates that differ
`'spearman'`	One minus the sample Spearman's rank correlation between observations (treated as sequences of values)
`@distfun`	Custom distance function handle. A distance function has the form function D2 = distfun(ZI,ZJ) % calculation of distance ... where `ZI` is a `1`-by-`n` vector containing a single observation. `ZJ` is an `m2`-by-`n` matrix containing multiple observations. `distfun` must accept a matrix `ZJ` with an arbitrary number of observations. `D2` is an `m2`-by-`1` vector of distances, and `D2(k)` is the distance between observations `ZI` and `ZJ(k,:)`. If your data is not sparse, you can generally compute distance more quickly by using a built-in distance instead of a function handle.

For more information, see Distance Metrics.

When you use the 'seuclidean', 'minkowski', or 'mahalanobis' distance metric, you can specify the additional name-value pair argument 'Scale', 'P', or 'Cov', respectively, to control the distance metrics.

Example: 'Distance','minkowski','P',3 specifies to use the Minkowski distance metric with an exponent of 3.

`P` — Exponent for Minkowski distance metric
`2` (default) | positive scalar

Exponent for the Minkowski distance metric, specified as the comma-separated pair consisting of 'P' and a positive scalar.

This argument is valid only if 'Distance' is 'minkowski'.

Example: 'P',3

Data Types: single | double

`Cov` — Covariance matrix for Mahalanobis distance metric
`cov(X,'omitrows')` (default) | positive definite matrix

Covariance matrix for the Mahalanobis distance metric, specified as the comma-separated pair consisting of 'Cov' and a positive definite matrix.

This argument is valid only if 'Distance' is 'mahalanobis'.

Example: 'Cov',eye(4)

Data Types: single | double

`Scale` — Scaling factors for standardized Euclidean distance metric
`std(X,'omitnan')` (default) | numeric vector of nonnegative values

Scaling factors for the standardized Euclidean distance metric, specified as the comma-separated pair consisting of 'Scale' and a numeric vector of nonnegative values.

Scale has length p (the number of columns in X), because each dimension (column) of X has a corresponding value in Scale. For each dimension of X, fsulaplacian uses the corresponding value in Scale to standardize the difference between observations.

This argument is valid only if 'Distance' is 'seuclidean'.

Data Types: single | double

`NumNeighbors` — Number of nearest neighbors
`log(size(X,1))` (default) | positive integer

Number of nearest neighbors used to construct the similarity graph, specified as the comma-separated pair consisting of 'NumNeighbors' and a positive integer.

Example: 'NumNeighbors',10

Data Types: single | double

`KernelScale` — Scale factor
`1` (default) | `'auto'` | positive scalar

Scale factor for the kernel, specified as the comma-separated pair consisting of 'KernelScale' and 'auto' or a positive scalar. The software uses the scale factor to transform distances to similarity measures. For more information, see Similarity Graph.

The 'auto' option is supported only for the 'euclidean' and 'seuclidean' distance metrics.
If you specify 'auto', then the software selects an appropriate scale factor using a heuristic procedure. This heuristic procedure uses subsampling, so estimates can vary from one call to another. To reproduce results, set a random number seed using rng before calling fsulaplacian.

Example: 'KernelScale','auto'

Output Arguments

collapse all

`idx` — Indices of features ordered by feature importance
numeric vector

Indices of the features in X ordered by feature importance, returned as a numeric vector. For example, if idx(3) is 5, then the third most important feature is the fifth column in X.

`scores` — Feature scores
numeric vector

Feature scores, returned as a numeric vector. A large score value in scores indicates that the corresponding feature is important. The values in scores have the same order as the features in X.

More About

collapse all

Similarity Graph

A similarity graph models the local neighborhood relationships between data points in X as an undirected graph. The nodes in the graph represent data points, and the edges, which are directionless, represent the connections between the data points.

If the pairwise distance Dist_i,j between any two nodes i and j is positive (or larger than a certain threshold), then the similarity graph connects the two nodes using an edge [2]. The edge between the two nodes is weighted by the pairwise similarity S_i,j, where $S_{i, j} = \exp (- {(\frac{D i s t_{i, j}}{σ})}^{2})$ , for a specified kernel scale σ value.

fsulaplacian constructs a similarity graph using the nearest neighbor method. The function connects points in X that are nearest neighbors. Use 'NumNeighbors' to specify the number of nearest neighbors.

Similarity Matrix

A similarity matrix is a matrix representation of a similarity graph. The n-by-n matrix $S = {(S_{i, j})}_{i, j = 1, \dots, n}$ contains pairwise similarity values between connected nodes in the similarity graph. The similarity matrix of a graph is also called an adjacency matrix.

The similarity matrix is symmetric because the edges of the similarity graph are directionless. A value of S_i,j = 0 means that nodes i and j of the similarity graph are not connected.

Degree Matrix

A degree matrix D_g is an n-by-n diagonal matrix obtained by summing the rows of the similarity matrix S. That is, the ith diagonal element of D_g is $D_{g} (i, i) = \sum_{j = 1}^{n} S_{i, j} .$

Laplacian Matrix

A Laplacian matrix, which is one way of representing a similarity graph, is defined as the difference between the degree matrix D_g and the similarity matrix S.

$L = D_{g} - S .$

Algorithms

collapse all

Laplacian Score

The fsulaplacian function ranks features using Laplacian scores [1] obtained from a nearest neighbor similarity graph.

fsulaplacian computes the values in scores as follows:

For each data point in X, define a local neighborhood using the nearest neighbor method, and find pairwise distances $D i s t_{i, j}$ for all points i and j in the neighborhood.
Convert the distances to the similarity matrix S using the kernel transformation $S_{i, j} = \exp (- {(\frac{D i s t_{i, j}}{σ})}^{2})$ , where σ is the scale factor for the kernel as specified by the 'KernelScale' name-value pair argument.
Center each feature by removing its mean.

${\tilde{x}}_{r} = x_{r} - \frac{x_{r}^{T} D_{g} 1}{1^{T} D_{g} 1} 1,$
where x_r is the rth feature, D_g is the degree matrix, and $1^{T} = {[1, \dots, 1]}^{T}$ .
Compute the score s_r for each feature.

$s_{r} = \frac{{\tilde{x}}_{r}^{T} S {\tilde{x}}_{r}}{{\tilde{x}}_{r}^{T} D_{g} {\tilde{x}}_{r}} .$

Note that [1] defines the Laplacian score as

$L_{r} = \frac{{\tilde{x}}_{r}^{T} L {\tilde{x}}_{r}}{{\tilde{x}}_{r}^{T} D_{g} {\tilde{x}}_{r}} = 1 - \frac{{\tilde{x}}_{r}^{T} S {\tilde{x}}_{r}}{{\tilde{x}}_{r}^{T} D_{g} {\tilde{x}}_{r}},$

where L is the Laplacian matrix, defined as the difference between D_g and S. The fsulaplacian function uses only the second term of this equation for the score value of scores so that a large score value indicates an important feature.

Selecting features using the Laplacian score is consistent with minimizing the value

$\frac{\sum_{i, j} {(x_{i r} - x_{j r})}^{2} S_{i, j}}{V a r (x_{r})},$

where x_ir represents the ith observation of the rth feature. Minimizing this value implies that the algorithm prefers features with large variance. Also, the algorithm assumes that two data points of an important feature are close if and only if the similarity graph has an edge between the two data points.

References

[1] He, X., D. Cai, and P. Niyogi. "Laplacian Score for Feature Selection." NIPS Proceedings. 2005.

[2] Von Luxburg, U. “A Tutorial on Spectral Clustering.” Statistics and Computing Journal. Vol.17, Number 4, 2007, pp. 395–416.

Version History

Introduced in R2019b

fsulaplacian

Syntax

Description

Examples

Rank Features by Importance

Rank Features Using Specified Similarity Matrix

Input Arguments

`X` — Input data
numeric matrix

Name-Value Arguments

`Similarity` — Similarity matrix
`[]` (empty matrix) (default) | symmetric matrix

`Distance` — Distance metric
character vector | string scalar | function handle

`P` — Exponent for Minkowski distance metric
`2` (default) | positive scalar

`Cov` — Covariance matrix for Mahalanobis distance metric
`cov(X,'omitrows')` (default) | positive definite matrix

`Scale` — Scaling factors for standardized Euclidean distance metric
`std(X,'omitnan')` (default) | numeric vector of nonnegative values

`NumNeighbors` — Number of nearest neighbors
`log(size(X,1))` (default) | positive integer

`KernelScale` — Scale factor
`1` (default) | `'auto'` | positive scalar

Output Arguments

`idx` — Indices of features ordered by feature importance
numeric vector

`scores` — Feature scores
numeric vector

More About

Similarity Graph

Similarity Matrix

Degree Matrix

Laplacian Matrix

Algorithms

Laplacian Score

References

Version History

See Also

Topics

fsulaplacian

Syntax

Description

Examples

Rank Features by Importance

Rank Features Using Specified Similarity Matrix

Input Arguments

X — Input data numeric matrix

Name-Value Arguments

Similarity — Similarity matrix [] (empty matrix) (default) | symmetric matrix

Distance — Distance metric character vector | string scalar | function handle

P — Exponent for Minkowski distance metric 2 (default) | positive scalar

Cov — Covariance matrix for Mahalanobis distance metric cov(X,'omitrows') (default) | positive definite matrix

Scale — Scaling factors for standardized Euclidean distance metric std(X,'omitnan') (default) | numeric vector of nonnegative values

NumNeighbors — Number of nearest neighbors log(size(X,1)) (default) | positive integer

KernelScale — Scale factor 1 (default) | 'auto' | positive scalar

Output Arguments

idx — Indices of features ordered by feature importance numeric vector

scores — Feature scores numeric vector

More About

Similarity Graph

Similarity Matrix

Degree Matrix

Laplacian Matrix

Algorithms

Laplacian Score

References

Version History

See Also

Topics

`X` — Input data
numeric matrix

`Similarity` — Similarity matrix
`[]` (empty matrix) (default) | symmetric matrix

`Distance` — Distance metric
character vector | string scalar | function handle

`P` — Exponent for Minkowski distance metric
`2` (default) | positive scalar

`Cov` — Covariance matrix for Mahalanobis distance metric
`cov(X,'omitrows')` (default) | positive definite matrix

`Scale` — Scaling factors for standardized Euclidean distance metric
`std(X,'omitnan')` (default) | numeric vector of nonnegative values

`NumNeighbors` — Number of nearest neighbors
`log(size(X,1))` (default) | positive integer

`KernelScale` — Scale factor
`1` (default) | `'auto'` | positive scalar

`idx` — Indices of features ordered by feature importance
numeric vector

`scores` — Feature scores
numeric vector