Main Content

gagerr

Gage repeatability and reproducibility study

collapse all in page

Syntax

gagerr(y,{part,operator})
gagerr(y,group)
gagerr(y,part)
gagerr(___,Name=Value)
gagerr(ax,___)
results = gagerr(___)
[results,stats] = gagerr(___)

Description

gagerr(y,{part,operator}) performs a Gage repeatability and reproducibility (R&R) study on the measurements y, collected by operator on part.

gagerr(y,group) performs an R&R study on the measurements y, where the numeric identifiers for the parts and operators are contained in the first and second columns, respectively, of the matrix group.

gagerr(y,part) performs an R&R study on the measurements y, collected on part. Use this syntax when all measurements are collected by a single operator.

gagerr(___,Name=Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in the previous syntaxes. For example, you can specify whether to display a bar graph of results, and set the specification limits for the precision-to-tolerance ratio (PTR) calculation.

example

gagerr(ax,___) plots into the axes specified by ax instead of the current axes (gca). (since R2024a)

results = gagerr(___) additionally returns the numeric matrix results, which contains the study results.

[results,stats] = gagerr(___) additionally returns the structure stats, which contains the number of distinct categories, the percentage of Gage R&R of total variations, and the PTR. If you do not set the specification limits (Spec), the PTR value is NaN.

Examples

collapse all

Open Live Script

Simulate a measurement data set by randomly generating 100 measurements y of three parts. Each measurement is collected by one of four randomly assigned operators.

rng(1234,"twister"); % For reproducibility
n = 100;
y = randn(n,1);                
part = randi([1,3],1,n);       
operator = randi([1,4],1,n);

Perform a Gage repeatability and reproducibility (R&R) study on this data set using a mixed ANOVA model without interactions.

gagerr(y,{part,operator},RandomOperator=false)
    {'Source'           }    {'Variance'}    {'% Variance'}    {'sigma' }    {'5.15*sigma'}    {'% 5.15*sigma'}
    {'Gage R&R'         }    {[  0.9535]}    {[   99.2515]}    {[0.9765]}    {[    5.0288]}    {[     99.6250]}
    {'  Repeatability'  }    {[  0.9535]}    {[   99.2515]}    {[0.9765]}    {[    5.0288]}    {[     99.6250]}
    {'  Reproducibility'}    {[       0]}    {[         0]}    {[     0]}    {[         0]}    {[           0]}
    {'Part'             }    {[  0.0072]}    {[    0.7485]}    {[0.0848]}    {[    0.4367]}    {[      8.6518]}
    {'Total'            }    {[  0.9607]}    {[       100]}    {[0.9801]}    {[    5.0477]}    {0x0 char      }

Number of distinct categories (NDC):0
% of Gage R&R of total variations (PRR): 99.63
Note: The last column of the above table does not have to sum to 100%

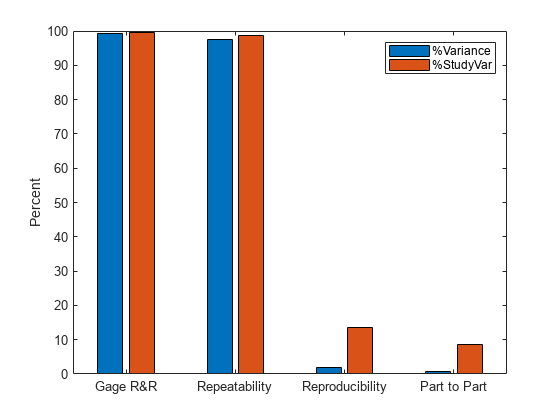
Figure contains an axes object. The axes object with ylabel Percent contains 2 objects of type bar. These objects represent %Variance, %StudyVar.

The software displays information and a bar graph summarizing the study results. Each row of the table contains statistics for a different source of variability in the measurement data. In this data set, the dominant source of variability is repeatability (the variation in the measurement value on the same part, obtained by the same operator). This source is responsible for 99.25% of the total measurement variance, and 99.63% of the total measurement standard deviation. The number of distinct categories is 0, indicating that the measurement system is not capable of distinguishing any groups within the measurement data.

Input Arguments

collapse all

Measurements, specified as a numeric column vector.

Data Types: single | double

Parts, specified as a categorical, character, or string array, a logical or numeric column vector, or a cell array of character vectors. part must have the same size as y. Each element of part contains an identifier for the part associated with the corresponding measurement in y.

Data Types: categorical | char | string | logical | single | double | cell

Operators, specified as a categorical, character, or string array, a logical or numeric column vector, or a cell array of character vectors. operator must have the same size as y. Each element of operator contains an identifier for the operator that collects the corresponding measurement in y.

Data Types: categorical | char | string | logical | single | double | cell

Parts and operators, specified as an n-by-2 numeric matrix, where n is the length of y. The first and second columns of group contain numeric identifiers for the part and operator, respectively, corresponding to the measurements in y.

Data Types: single | double

Axes for the plot, specified as an Axes object. If you do not specify ax, then gagerr creates the plot using the current axes. For more information on creating an Axes object, see axes.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: results=gagerr(y,group,PrintTable="off") specifies to suppress the display of command-line output.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

ANOVA model type, specified as one of the values in this table.

ValueDescription
"linear" (default)Main effects only
"interaction"Main effects plus two-factor interactions between operator and part
"nested"operator is nested in part. Use this model when operators are assigned to specific parts, and the operators measure only those specific parts. For more information, see Other ANOVA Models.

If you specify "linear" or "interaction", gagerr calls the anovan function with the specified value of Model. If you specify "nested", gagerr calls anovan with model="linear" and nested=[0 0; 1 0].

If you specify part but do not specify operator in the call to gagerr, you cannot specify "interaction" or "nested".

Example: Model="interaction"

Data Types: char | string

Indicator for random operators, specified as a numeric or logical 1 (true) or 0 (false). If you specify RandomOperator=false, the software uses a mixed-effects model, where part is a random effect and operator is a fixed effect.

Example: RandomOperator=false

Data Types: logical

Lower and upper specification limits, specified as a two-element numeric vector. If you specify Spec, the software computes the precision-to-tolerance ratio (PTR) using the formula PTR=5.15 σGRR/|(S2−S1)|, where σGRR is the Gage R&R standard deviation, and S1 and S2 are the first and second elements of Spec, respectively. If you do not specify Spec, PTR is NaN. For more information about PTR, see Gage R&R Study.

Example: Spec=[0.1 0.9]

Data Types: single | double

Flag to display the results output, specified as "on" or "off". For more information about the results output, see Gage R&R Study.

Example: PrintTable="off"

Data Types: char | string

Flag to display a bar graph of the results, specified as "on" or "off". For more information about the bar graph results, see Gage R&R Study.

Example: PrintGraph="off"

Data Types: char | string

Output Arguments

collapse all

Study results, returned as a 6-by-5 numeric matrix where the rows contain metrics for individual sources of variability in the measurement system. The rows of results are described below.

RowDescription
Gage R&RTotal measurement variation due to repeatability and reproducibility sources
RepeatabilityVariation in the measurements of the same part, collected by the same operator
ReproducibilityVariation in the measurements of the same part, collected by different operators
OperatorVariation in the measurements collected by the same operator
Part*OperatorVariation in the measurements due to the two-factor interactions of parts and operators. The variation is zero unless Model is "interaction".
Part-to-partVariation among the set of parts

The columns of results are described below.

ColumnDescription
SourceVariability source
VarianceVariance
% VariancePercentage of the total variance
sigmaStandard deviation (square root of the variance)
5.15*sigmaStudy variance, which is 5.15 times the standard deviation
% 5.15*sigmaPercentage of the total study variance

Summary statistics, returned as a structure with these fields:

  • ndc — Number of distinct categories

  • prr — Percentage of Gage R&R of total variations

  • ptr — Precision-to-tolerance ratio

If you do not specify Spec, then ptr is NaN. For more information on the summary statistics, see Gage R&R Study.

More About

collapse all

Gage R&R Study

A Gage repeatability and reproducibility (R&R) study uses one- or two-way analysis of variance (see anovan) to assess the precision of a measurement system. In a typical system, a group of operators use gages to obtain multiple measurements of a set of items (parts) under the same conditions, if possible. If a system has high precision, the measurements of an individual part are narrowly scattered around a single value. There are several possible sources of variability in a measurement system.

Variability SourceDescription
RepeatabilityVariation in the measurements of the same part, collected by the same operator
OperatorVariation in the measurements collected by the same operator
Part*OperatorVariation in the measurements due to the interactions of parts and operators
ReproducibilitySum of Operator and Part*Operator
Gage R&RTotal measurement variation due to repeatability and reproducibility
Part-to-partVariation among the set of parts.

The total variability in a measurement system is the sum of Gage R&R variability and part-to-part variability.

Each of the variability sources can be characterized by a statistical metric. Common metrics are the variance, standard deviation (square root of the variance), percentage of the total variance, and percentage of the total standard deviation. The study variance is a measure of all variability in the measurement system due to repeatability and reproducibility, and is defined as 5.15 times the Gage R&R standard deviation. The factor 5.15 corresponds to the number of standard deviations that span the middle 99% of a normally distributed population.

Three common summary metrics describe the capability of a measurement system to distinguish the parts from each other, based on the measurement data:

  • The number of distinct categories (NDC) is a measure of how many groups the system can distinguish within the measurement data. NDC is equal to 2 times the ratio of part-to-part standard deviation to Gage R&R standard deviation. An NDC value of 5 or larger is indicative of a capable measurement system. A system with an NDC value smaller than 2 is not capable. For example, if a measurement system has NDC=3, the measurements can be divided into three groups, such as low, middle, and high.

  • The percentage of Gage R&R of total variations (PRR) is the fraction of the total standard deviation that is due to Gage R&R variability. In general, a system with PRR less than 10% is capable, while a PRR value greater than 30% indicates that the system is not capable.

  • The precision-to-tolerance ratio (PTR) compares the variability in the measurement system to the specified tolerance (Spec). In general, a system with PTR less than 0.1 is capable, while a PTR value greater than 0.3 indicates that the system is not capable. For example, if the lower and upper specification limits for the set of parts are 1 and 20, respectively, and the standard deviation of the measurements due to Gage R&R is 0.3, the PTR value is 0.08, indicating a capable system.

References

[1] Burdick, Richard K., Connie M. Borror, and Douglas C. Montgomery. Design and Analysis of Gauge R&R Studies: Making Decisions with Confidence Intervals in Random and Mixed ANOVA Models. ASA-SIAM Series on Statistics and Applied Probability. Philadelphia, Pa. : Alexandria, Va: Society for Industrial Applied Mathematics ; American Statistical Association, 2005.

Version History

Introduced in R2006b

expand all

See Also

Topics