updateMetrics
Update performance metrics in kernel incremental learning model given new data
Since R2022a
Description
Given streaming data, updateMetrics measures the performance of
a configured incremental learning model for kernel regression (incrementalRegressionKernel object) or binary kernel classification (incrementalClassificationKernel object). updateMetrics stores
the performance metrics in the output model.
updateMetrics allows for flexible incremental learning. After you call
the function to update model performance metrics on an incoming chunk of data, you can perform
other actions before you train the model to the data. For example, you can decide whether you
need to train the model based on its performance on a chunk of data. Alternatively, you can
both update model performance metrics and train the model on the data as it arrives, in one
call, by using the updateMetricsAndFit
function.
To measure the model performance on a specified batch of data, call loss
instead.
Mdl = updateMetrics(Mdl,X,Y)Mdl, which is the input incremental learning model Mdl modified to contain the model performance metrics on the incoming
predictor and response data, X and Y
respectively.
When the input model is warm (Mdl.IsWarm is
true), updateMetrics overwrites previously computed
metrics, stored in the Metrics property, with the new values. Otherwise,
updateMetrics stores NaN values in
Metrics instead.
The input and output models have the same data type.
Examples
Train a kernel model for binary classification by using fitckernel, convert it to an incremental learner, and then track its performance to streaming data.
Load and Preprocess Data
Load the human activity data set. Randomly shuffle the data.
load humanactivity rng(1) % For reproducibility n = numel(actid); idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Responses can be one of five classes: Sitting, Standing, Walking, Running, or Dancing. Dichotomize the response by identifying whether the subject is moving (actid > 2).
Y = Y > 2;
Train Kernel Model for Binary Classification
Fit a kernel model for binary classification to a random sample of half the data.
idxtt = randsample([true false],n,true); TTMdl = fitckernel(X(idxtt,:),Y(idxtt))
TTMdl =
ClassificationKernel
ResponseName: 'Y'
ClassNames: [0 1]
Learner: 'svm'
NumExpansionDimensions: 2048
KernelScale: 1
Lambda: 8.2967e-05
BoxConstraint: 1
Properties, Methods
TTMdl is a ClassificationKernel model object representing a traditionally trained kernel model for binary classification.
Convert Trained Model
Convert the traditionally trained classification model to a model for incremental learning.
IncrementalMdl = incrementalLearner(TTMdl)
IncrementalMdl =
incrementalClassificationKernel
IsWarm: 1
Metrics: [1×2 table]
ClassNames: [0 1]
ScoreTransform: 'none'
NumExpansionDimensions: 2048
KernelScale: 1
Properties, Methods
IncrementalMdl is an incrementalClassificationKernel model. The model display shows that the model is warm (IsWarm is 1). Therefore, updateMetrics can track model performance metrics given data.
Track Performance Metrics
Track the model performance on the rest of the data by using the updateMetrics function. Simulate a data stream by processing 50 observations at a time. At each iteration:
Call
updateMetricsto update the cumulative and window classification error of the model given the incoming chunk of observations. Overwrite the previous incremental model to update the losses in theMetricsproperty. Note that the function does not fit the model to the chunk of data—the chunk is "new" data for the model.Store the classification error and number of training observations.
% Preallocation idxil = ~idxtt; nil = sum(idxil); numObsPerChunk = 50; nchunk = floor(nil/numObsPerChunk); ce = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]); numtrainobs = [zeros(nchunk,1)]; Xil = X(idxil,:); Yil = Y(idxil); % Incremental fitting for j = 1:nchunk ibegin = min(nil,numObsPerChunk*(j-1) + 1); iend = min(nil,numObsPerChunk*j); idx = ibegin:iend; IncrementalMdl = updateMetrics(IncrementalMdl,Xil(idx,:),Yil(idx)); ce{j,:} = IncrementalMdl.Metrics{"ClassificationError",:}; numtrainobs(j) = IncrementalMdl.NumTrainingObservations; end
IncrementalMdl is an incrementalClassificationKernel model object that has tracked the model performance to observations in the data stream.
Plot a trace plot of the number of training observations and the performance metrics on separate tiles.
t = tiledlayout(2,1); nexttile plot(numtrainobs) ylabel("Number of Training Observations") xlim([0 nchunk]) nexttile plot(ce.Variables) xlim([0 nchunk]) ylabel("Classification Error") legend(ce.Properties.VariableNames,Location="best") xlabel(t,"Iteration")
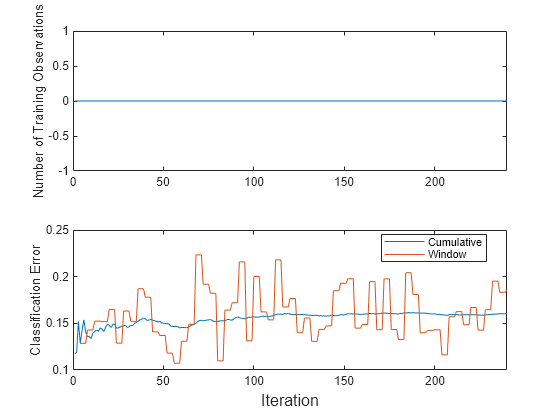
The cumulative loss is stable, whereas the window loss jumps. The number of training observations does not change because updateMetrics does not fit the model to the data.
Configure incremental learning options for an incrementalClassificationKernel model object when you call the incrementalClassificationKernel function. Track the model performance on streaming data, and fit the model to the data. Specify observation weights when you call incremental learning functions.
Create an incremental kernel model for binary classification. Specify an estimation period of 5000 observations and the stochastic gradient descent (SGD) solver.
Mdl = incrementalClassificationKernel(EstimationPeriod=5000,Solver="sgd")Mdl =
incrementalClassificationKernel
IsWarm: 0
Metrics: [1×2 table]
ClassNames: [1×0 double]
ScoreTransform: 'none'
NumExpansionDimensions: 0
KernelScale: 1
Properties, Methods
Mdl is an incrementalClassificationKernel model. All its properties are read-only.
The model display shows that the model is not warm (IsWarm is 0). Determine the size of the metrics warm-up period by displaying model properties.
mwp = Mdl.MetricsWarmupPeriod
mwp = 1000
Determine the number of observations that incremental fitting functions, such as fit, must process before measuring the performance of the model.
numObsBeforeMetrics = Mdl.MetricsWarmupPeriod + Mdl.EstimationPeriod
numObsBeforeMetrics = 6000
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Responses can be one of five classes: Sitting, Standing, Walking, Running, or Dancing. Dichotomize the response by identifying whether the subject is moving (actid > 2).
Y = Y > 2;
Suppose that the data collected when the subject was not moving (Y = false) has double the quality than when the subject was moving. Create a weight variable that attributes 2 to observations collected from a still subject, and 1 to a moving subject.
W = ones(n,1) + ~Y;
Perform incremental learning. At each iteration:
Simulate a data stream by processing a chunk of 50 observations.
Measure model performance metrics on the incoming chunk using
updateMetrics. Specify the corresponding observation weights and overwrite the input model.Fit the model to the incoming chunk by using the
fitfunction. Specify the corresponding observation weights and overwrite the input model.Store the misclassification error rate and number of training observations to see how they evolve during incremental learning.
% Preallocation numObsPerChunk = 50; nchunk = floor(n/numObsPerChunk); ce = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]); numtrainobs = [zeros(nchunk,1)]; % Incremental fitting for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; Mdl = updateMetrics(Mdl,X(idx,:),Y(idx),Weights=W(idx)); ce{j,:} = Mdl.Metrics{"ClassificationError",:}; Mdl = fit(Mdl,X(idx,:),Y(idx),Weights=W(idx)); numtrainobs(j) = Mdl.NumTrainingObservations; end
Mdl is an incrementalClassificationKernel model object trained on all the data in the stream.
Plot a trace plot of the number of training observations and the performance metrics on separate tiles.
t = tiledlayout(2,1); nexttile plot(numtrainobs) ylabel("Number of Training Observations") xline(Mdl.EstimationPeriod/numObsPerChunk,'-.') xlim([0 nchunk]) nexttile plot(ce.Variables) ylabel('ClassificationError') xline(Mdl.EstimationPeriod/numObsPerChunk,'-.') xline(numObsBeforeMetrics/numObsPerChunk,'--') xlim([0 nchunk]); legend(ce.Properties.VariableNames,Location="best") xlabel(t,'Iteration')
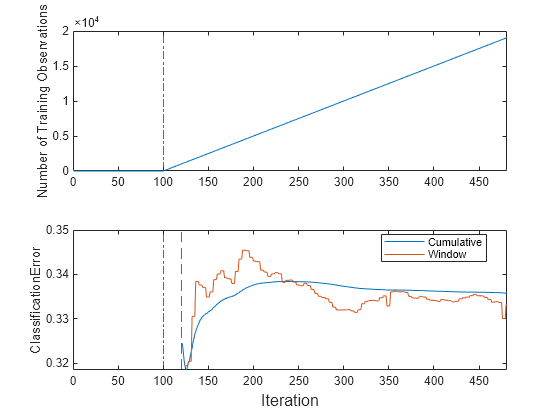
mdlIsWarm = numObsBeforeMetrics/numObsPerChunk
mdlIsWarm = 120
The plot suggests that fit does not fit the model to the data or update the parameters until after the estimation period. Also, updateMetrics does not track the classification error until after the estimation and metrics warm-up periods (120 chunks).
Incrementally train a kernel regression model only when its performance degrades.
Load and shuffle the 2015 NYC housing data set. For more details on the data, see NYC Open Data.
load NYCHousing2015 rng(1) % For reproducibility n = size(NYCHousing2015,1); shuffidx = randsample(n,n); NYCHousing2015 = NYCHousing2015(shuffidx,:);
Extract the response variable SALEPRICE from the table. For numerical stability, scale SALEPRICE by 1e6.
Y = NYCHousing2015.SALEPRICE/1e6; NYCHousing2015.SALEPRICE = [];
To reduce computational cost for this example, remove the NEIGHBORHOOD column, which contains a categorical variable with 254 categories.
NYCHousing2015.NEIGHBORHOOD = [];
Create dummy variable matrices from the other categorical predictors.
catvars = ["BOROUGH","BUILDINGCLASSCATEGORY"]; dumvarstbl = varfun(@(x)dummyvar(categorical(x)),NYCHousing2015, ... InputVariables=catvars); dumvarmat = table2array(dumvarstbl); NYCHousing2015(:,catvars) = [];
Treat all other numeric variables in the table as predictors of sales price. Concatenate the matrix of dummy variables to the rest of the predictor data.
idxnum = varfun(@isnumeric,NYCHousing2015,OutputFormat="uniform");
X = [dumvarmat NYCHousing2015{:,idxnum}];Configure a kernel regression model for incremental learning so that it does not have an estimation or metrics warm-up period. Specify a metrics window size of 1000. Prepare the model for updateMetrics by fitting it to the first 100 observations.
Mdl = incrementalRegressionKernel(EstimationPeriod=0, ...
MetricsWarmupPeriod=0,MetricsWindowSize=1000);
initobs = 100;
Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs));Mdl is an incrementalRegressionKernel model object.
Perform incremental learning, with conditional fitting, by following this procedure for each iteration:
Simulate a data stream by processing a chunk of 100 observations at a time.
Update the model performance by computing the epsilon insensitive loss, within a 200 observation window.
Fit the model to the chunk of data only when the loss more than doubles from the minimum loss experienced.
When tracking performance and fitting, overwrite the previous incremental model.
Store the epsilon insensitive loss and number of training observations to see how they evolve during training.
Track when
fittrains the model.
% Preallocation numObsPerChunk = 100; nchunk = floor((n - initobs)/numObsPerChunk); ei = array2table(nan(nchunk,2),VariableNames=["Cumulative","Window"]); numtrainobs = zeros(nchunk,1); trained = false(nchunk,1); % Incremental fitting for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs); iend = min(n,numObsPerChunk*j + initobs); idx = ibegin:iend; Mdl = updateMetrics(Mdl,X(idx,:),Y(idx)); ei{j,:} = Mdl.Metrics{"EpsilonInsensitiveLoss",:}; minei = min(ei{:,2}); pdiffloss = (ei{j,2} - minei)/minei*100; if pdiffloss > 100 Mdl = fit(Mdl,X(idx,:),Y(idx)); trained(j) = true; end numtrainobs(j) = Mdl.NumTrainingObservations; end
Mdl is an incrementalRegressionKernel model object trained on all the data in the stream.
To see how the number of training observations and model performance evolve during training, plot them on separate tiles.
t = tiledlayout(2,1); nexttile plot(numtrainobs) hold on plot(find(trained),numtrainobs(trained),"r.") xlim([0 nchunk]) ylabel("Number of Training Observations") legend("Number of Training Observations","Training occurs",Location="best") hold off nexttile plot(ei.Variables) xlim([0 nchunk]) ylabel("Epsilon Insensitive Loss") legend(ei.Properties.VariableNames) xlabel(t,"Iteration")
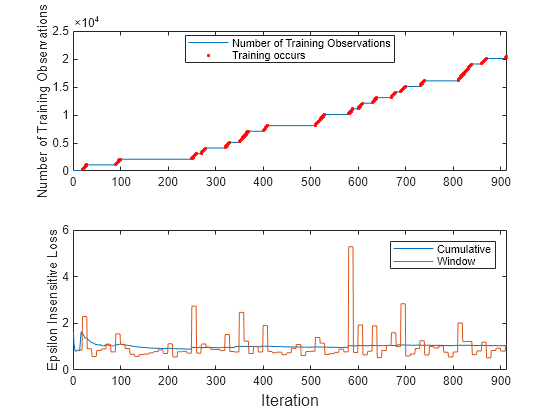
The trace plot of the number of training observations shows periods of constant values, during which the loss does not double from the minimum experienced.
Input Arguments
Incremental learning model whose performance is measured, specified as an incrementalClassificationKernel or incrementalRegressionKernel model object. You can create
Mdl directly or by converting a supported, traditionally trained
machine learning model using the incrementalLearner function. For
more details, see the corresponding reference page.
If Mdl.IsWarm is false,
updateMetrics does not track the performance of the model. You must
fit Mdl to Mdl.EstimationPeriod +
Mdl.MetricsWarmupPeriod observations by passing Mdl and
the data to fit before
updateMetrics can track performance metrics. For more details, see
Performance Metrics.
Chunk of predictor data, specified as a floating-point matrix of n
observations and Mdl.NumPredictors predictor variables.
The length of the observation labels Y and the number of observations in X must be equal; Y( is the label of observation j (row) in j)X.
Note
If
Mdl.NumPredictors= 0,updateMetricsinfers the number of predictors fromX, and sets the corresponding property of the output model. Otherwise, if the number of predictor variables in the streaming data changes fromMdl.NumPredictors,updateMetricsissues an error.updateMetricssupports only floating-point input predictor data. If your input data includes categorical data, you must prepare an encoded version of the categorical data. Usedummyvarto convert each categorical variable to a numeric matrix of dummy variables. Then, concatenate all dummy variable matrices and any other numeric predictors. For more details, see Dummy Variables.
Data Types: single | double
Chunk of responses (labels), specified as a categorical, character, or string array, a logical or floating-point vector, or a cell array of character vectors for classification problems; or a floating-point vector for regression problems.
The length of the observation labels Y and the number of
observations in X must be equal;
Y( is the label of observation
j (row) in j)X.
For classification problems:
updateMetricssupports binary classification only.When the
ClassNamesproperty of the input modelMdlis nonempty, the following conditions apply:If
Ycontains a label that is not a member ofMdl.ClassNames,updateMetricsissues an error.The data type of
YandMdl.ClassNamesmust be the same.
Data Types: char | string | cell | categorical | logical | single | double
Chunk of observation weights, specified as a floating-point vector of positive values.
updateMetrics weighs the observations in X
with the corresponding values in weights. The size of
weights must equal n, the number of
observations in X.
By default, weights is
ones(.n,1)
For more details, including normalization schemes, see Observation Weights.
Data Types: double | single
Note
If an observation (predictor or label) or weight contains at
least one missing (NaN) value, updateMetrics ignores the
observation. Consequently, updateMetrics uses fewer than n
observations to compute the model performance, where n is the number of
observations in X.
Output Arguments
Updated incremental learning model, returned as an incremental learning model object
of the same data type as the input model Mdl, either incrementalClassificationKernel or incrementalRegressionKernel.
If the model is not warm, updateMetrics does
not compute performance metrics. As a result, the Metrics property of
Mdl remains completely composed of NaN values. If the
model is warm, updateMetrics computes the cumulative and window performance
metrics on the new data X and Y, and overwrites the
corresponding elements of Mdl.Metrics. All other properties of the input
model Mdl carry over to the output model Mdl. For more details, see
Performance Metrics.
Tips
Unlike traditional training, incremental learning might not have a separate test (holdout) set. Therefore, to treat each incoming chunk of data as a test set, pass the incremental model and each incoming chunk to
updateMetricsbefore training the model on the same data usingfit.
Algorithms
updateMetricsandupdateMetricsAndFittrack model performance metrics, specified by the row labels of the table inMdl.Metrics, from new data only when the incremental model is warm (IsWarmproperty istrue). An incremental model is warm afterfitorupdateMetricsAndFitfits the incremental model toMdl.MetricsWarmupPeriodobservations, which is the metrics warm-up period.If
Mdl.EstimationPeriod> 0, thefitandupdateMetricsAndFitfunctions estimate hyperparameters before fitting the model to data. Therefore, the functions must process an additionalEstimationPeriodobservations before the model starts the metrics warm-up period.The
Mdl.Metricsproperty stores two forms of each performance metric as variables (columns) of a table,CumulativeandWindow, with individual metrics in rows. When the incremental model is warm,updateMetricsandupdateMetricsAndFitupdate the metrics at the following frequencies:Cumulative— The functions compute cumulative metrics since the start of model performance tracking. The functions update metrics every time you call the functions and base the calculation on the entire supplied data set.Window— The functions compute metrics based on all observations within a window determined by theMdl.MetricsWindowSizeproperty.Mdl.MetricsWindowSizealso determines the frequency at which the software updatesWindowmetrics. For example, ifMdl.MetricsWindowSizeis 20, the functions compute metrics based on the last 20 observations in the supplied data (X((end – 20 + 1):end,:)andY((end – 20 + 1):end)).Incremental functions that track performance metrics within a window use the following process:
Store a buffer of length
Mdl.MetricsWindowSizefor each specified metric, and store a buffer of observation weights.Populate elements of the metrics buffer with the model performance based on batches of incoming observations, and store corresponding observation weights in the weights buffer.
When the buffer is filled, overwrite
Mdl.Metrics.Windowwith the weighted average performance in the metrics window. If the buffer is overfilled when the function processes a batch of observations, the latest incomingMdl.MetricsWindowSizeobservations enter the buffer, and the earliest observations are removed from the buffer. For example, supposeMdl.MetricsWindowSizeis 20, the metrics buffer has 10 values from a previously processed batch, and 15 values are incoming. To compose the length 20 window, the function uses the measurements from the 15 incoming observations and the latest 5 measurements from the previous batch.
The software omits an observation with a
NaNprediction (score for classification and response for regression) when computing theCumulativeandWindowperformance metric values.
For classification problems, if the prior class probability distribution is known (in other words, the prior distribution is not empirical), updateMetrics normalizes observation weights to sum to the prior class probabilities in the respective classes. This action implies that observation weights are the respective prior class probabilities by default.
For regression problems or if the prior class probability distribution is empirical, the software normalizes the specified observation weights to sum to 1 each time you call updateMetrics.
Version History
Introduced in R2022a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)