RegressionQuantileLinear

Quantile linear regression model

Since R2024b

Description

A RegressionQuantileLinear object is a trained quantile linear regression model. For each quantile (Quantiles), the object stores the estimated linear model coefficients (Beta) and estimated bias term (Bias). The object also contains the regularization strength used for all quantiles (Lambda).

After training a RegressionQuantileLinear model object, you can use the loss object function to compute the quantile loss, and the predict object function to predict the response for new data.

Creation

Create a RegressionQuantileLinear object by using the fitrqlinear function.

Properties

expand all

Linear Regression Properties

`Quantiles` — Quantiles
vector of values in the range [0,1]

This property is read-only.

Quantiles used to train the quantile linear regression model, returned as a vector of values in the range [0,1].

Data Types: double

`Beta` — Linear coefficient estimates
numeric matrix

This property is read-only.

Linear coefficient estimates, returned as a numeric matrix. Each row corresponds to an expanded predictor (ExpandedPredictorNames), and each column corresponds to a quantile (Quantiles).

Data Types: double

`Bias` — Estimated bias terms
numeric vector

This property is read-only.

Estimated bias terms or model intercepts, returned as a numeric vector. Each element corresponds to a quantile (Quantiles).

Data Types: double

`Lambda` — Regularization term strength
nonnegative scalar

This property is read-only.

Regularization term strength for the ridge (L2) penalty, returned as a nonnegative scalar. The software uses the same regularization term strength for all quantiles.

Data Types: double | single

`Solver` — Objective function minimization technique
`'bfgs'` | `'lbfgs'`

This property is read-only.

Objective function minimization technique used to train the quantile linear regression model, returned as 'bfgs' or 'lbfgs'.

Data Types: char

`ModelParameters` — Parameter values used to train model
`QuantileLinearParams` object

This property is read-only.

Parameter values used to train the quantile linear regression model, returned as a QuantileLinearParams object. ModelParameters contains parameter values such as the name-value arguments used to train the model.

Access the properties of ModelParameters by using dot notation. For example, you can access the initial linear coefficient estimates used to train a model Mdl by using Mdl.ModelParameters.Beta.

`ConvergenceInfo` — Convergence information
structure array

This property is read-only.

Convergence information, returned as a structure array.

Field	Description
`Lambda`	Regularization term strength
`Objective`	Objective function value for each quantile when the training optimization ends
`IterationLimit`	Maximum number of training optimization iterations
`NumIterations`	Number of iterations used to train the model for each quantile
`GradientNorm`	Gradient magnitude at the last iteration for each quantile
`GradientTolerance`	Absolute gradient tolerance
`RelativeChangeInBeta`	Relative change in the linear coefficients at the last iteration for each quantile
`BetaTolerance`	Relative tolerance on the linear coefficients and the bias term
`TerminationCode`	Code for `TerminationStatus`
`TerminationStatus`	Criterion for ending the training optimization
`History`	Training history
`FitTime`	Total time spent fitting the model for each quantile (in seconds)

Data Types: struct

Predictor Properties

`PredictorNames` — Predictor variable names
cell array of character vectors

This property is read-only.

Predictor variable names, returned as a cell array of character vectors. The order of the elements of PredictorNames corresponds to the order in which the predictor names appear in the training data.

Data Types: cell

`CategoricalPredictors` — Categorical predictor indices
vector of positive integers | `[]`

This property is read-only.

Categorical predictor indices, returned as a vector of positive integers. Assuming that the predictor data contains observations in rows, CategoricalPredictors contains index values corresponding to the columns of the predictor data that contain categorical predictors. If none of the predictors are categorical, then this property is empty ([]).

Data Types: double

`ExpandedPredictorNames` — Expanded predictor names
cell array of character vectors

This property is read-only.

Expanded predictor names, returned as a cell array of character vectors. If the model uses encoding for categorical variables, then ExpandedPredictorNames includes the names that describe the expanded variables. Otherwise, ExpandedPredictorNames is the same as PredictorNames.

Data Types: cell

`Mu` — Predictor means
numeric vector | `[]`

This property is read-only.

Predictor means, returned as a numeric vector. If you set Standardize to 1 or true when you train the linear model, then the length of the Mu vector is equal to the number of expanded predictors (ExpandedPredictorNames). The vector contains 0 values for dummy variables corresponding to expanded categorical predictors.

If you set Standardize to 0 or false when you train the linear model, then the Mu value is an empty vector ([]).

Data Types: double

`Sigma` — Predictor standard deviations
numeric vector | `[]`

This property is read-only.

Predictor standard deviations, returned as a numeric vector. If you set Standardize to 1 or true when you train the linear model, then the length of the Sigma vector is equal to the number of expanded predictors (ExpandedPredictorNames). The vector contains 1 values for dummy variables corresponding to expanded categorical predictors.

If you set Standardize to 0 or false when you train the linear model, then the Sigma value is an empty vector ([]).

Data Types: double

`X` — Unstandardized predictors
numeric matrix | table

This property is read-only.

Unstandardized predictors used to train the linear model, returned as a numeric matrix or table. X retains its original orientation, with observations in rows or columns depending on the value of the ObservationsIn name-value argument in the call to fitrqlinear.

Data Types: single | double | table

Response Properties

`ResponseName` — Response variable name
character vector

This property is read-only.

Response variable name, returned as a character vector.

Data Types: char

`Y` — Response values
numeric vector

This property is read-only.

Response values used to train the model, returned as a numeric vector. Each row of Y represents the response value of the corresponding observation in X.

Data Types: single | double

`ResponseTransform` — Response transformation function
`'none'` | function handle

Response transformation function, specified as 'none' or a function handle. ResponseTransform describes how the software transforms raw response values.

For a MATLAB^® function or a function that you define, enter its function handle. For example, you can enter Mdl.ResponseTransform = @function, where function accepts a numeric vector of the original responses and returns a numeric vector of the same size containing the transformed responses.

Data Types: char | function_handle

Other Data Properties

`NumObservations` — Number of observations
positive numeric scalar

This property is read-only.

Number of observations in the training data stored in X and Y, returned as a positive numeric scalar.

Data Types: double

`RowsUsed` — Observations of original training data stored
logical vector | `[]`

This property is read-only.

Observations of the original training data stored in the model, returned as a logical vector. This property is empty if all observations are stored in X and Y.

Data Types: logical

`W` — Observation weights
numeric vector

This property is read-only.

Observation weights used to train the model, returned as an n-by-1 numeric vector. n is the number of observations (NumObservations).

The software normalizes the observation weights specified by the Weights name-value argument in the call to fitrqlinear so that the elements of W sum to 1.

Data Types: single | double

Object Functions

`loss`	Loss for quantile linear regression model
`predict`	Predict response for quantile linear regression model

Examples

collapse all

Fit Quantile Linear Regression Model

Open Live Script

Fit a quantile linear regression model using the 0.25, 0.50, and 0.75 quantiles.

Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a matrix X containing the predictor variables Acceleration, Displacement, Horsepower, and Weight. Store the response variable MPG in the variable Y.

load carbig
X = [Acceleration,Displacement,Horsepower,Weight];
Y = MPG;

Delete rows of X and Y where either array has missing values.

R = rmmissing([X Y]);
X = R(:,1:end-1);
Y = R(:,end);

Partition the data into training data (XTrain and YTrain) and test data (XTest and YTest). Reserve approximately 20% of the observations for testing, and use the rest of the observations for training.

rng(0,"twister") % For reproducibility of the partition
c = cvpartition(length(Y),"Holdout",0.20);

trainingIdx = training(c);
XTrain = X(trainingIdx,:);
YTrain = Y(trainingIdx);

testIdx = test(c);
XTest = X(testIdx,:);
YTest = Y(testIdx);

Train a quantile linear regression model. Specify to use the 0.25, 0.50, and 0.75 quantiles (that is, the lower quartile, median, and upper quartile). To improve the model fit, change the beta tolerance to 1e-6 instead of the default value 1e-4. Use a ridge (L2) regularization term of 1. Adding a regularization term can help prevent quantile crossing.

Mdl = fitrqlinear(XTrain,YTrain,Quantiles=[0.25,0.50,0.75], ...
    BetaTolerance=1e-6,Lambda=1)

Mdl = 
  RegressionQuantileLinear
             ResponseName: 'Y'
    CategoricalPredictors: []
        ResponseTransform: 'none'
                     Beta: [4x3 double]
                     Bias: [17.0004 23.0029 29.5243]
                Quantiles: [0.2500 0.5000 0.7500]

Mdl is a RegressionQuantileLinear model object. You can use dot notation to access the properties of Mdl. For example, Mdl.Beta and Mdl.Bias contain the linear coefficient estimates and estimated bias terms, respectively. Each column of Mdl.Beta corresponds to one quantile, as does each element of Mdl.Bias.

In this example, you can use the linear coefficient estimates and estimated bias terms directly to predict the test set responses for each of the three quantiles in Mdl.Quantiles. In general, you can use the predict object function to make quantile predictions.

predictedY = XTest*Mdl.Beta + Mdl.Bias

predictedY = 78×3

   12.3963   16.2569   19.5263
    5.8328   10.1568   12.6058
   17.1726   20.6398   24.9748
   23.3790   28.1122   31.3617
   17.0036   22.5314   23.0539
   16.6120   17.0713   20.1062
   10.9274   12.3302   13.2707
   14.9130   14.6659   12.7100
   16.3103   17.7497   20.8477
   19.6229   25.7109   30.5389
      ⋮

isequal(predictedY,predict(Mdl,XTest))

ans = logical
   1

Each column of predictedY corresponds to a separate quantile (0.25, 0.5, or 0.75).

Visualize the predictions of the quantile linear regression model. First, create a grid of predictor values.

minX = floor(min(X))

minX = 1×4

           8          68          46        1613

maxX = ceil(max(X))

maxX = 1×4

          25         455         230        5140

gridX = zeros(100,size(X,2));
for p = 1:size(X,2)
    gridp = linspace(minX(p),maxX(p))';
    gridX(:,p) = gridp;
end

Next, use the trained model Mdl to predict the response values for the grid of predictor values.

gridY = predict(Mdl,gridX)

gridY = 100×3

   20.8073   25.4104   29.1436
   20.6991   25.2907   29.0251
   20.5909   25.1711   28.9066
   20.4828   25.0514   28.7881
   20.3746   24.9318   28.6696
   20.2664   24.8121   28.5512
   20.1583   24.6924   28.4327
   20.0501   24.5728   28.3142
   19.9419   24.4531   28.1957
   19.8337   24.3335   28.0772
      ⋮

For each observation in gridX, the predict object function returns predictions for the quantiles in Mdl.Quantiles.

View the gridY predictions for the second predictor (Displacement). Compare the quantile predictions to the true test data values.

predictorIdx = 2;
plot(XTest(:,predictorIdx),YTest,".")
hold on
plot(gridX(:,predictorIdx),gridY(:,1))
plot(gridX(:,predictorIdx),gridY(:,2))
plot(gridX(:,predictorIdx),gridY(:,3))
hold off
xlabel("Predictor (Displacement)")
ylabel("Response (MPG)")
legend(["True values","0.25 predicted values", ...
    "0.50 predicted values","0.75 predicted values"])
title("Test Data")

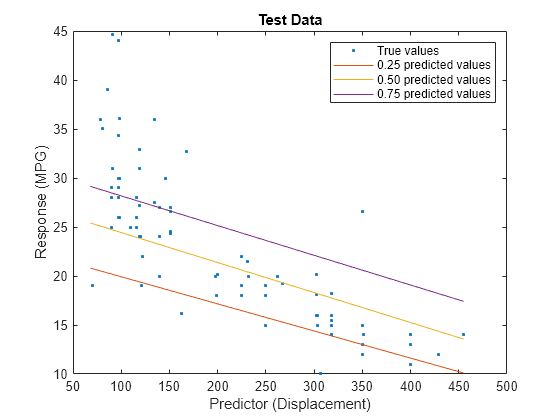
Figure contains an axes object. The axes object with title Test Data, xlabel Predictor (Displacement), ylabel Response (MPG) contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent True values, 0.25 predicted values, 0.50 predicted values, 0.75 predicted values.

The red line shows the predictions for the 0.25 quantile, the yellow line shows the predictions for the 0.50 quantile, and the purple line shows the predictions for the 0.75 quantile. The blue points indicate the true test data values.

Notice that the quantile prediction lines do not cross each other.

Version History

Introduced in R2024b

RegressionQuantileLinear

Description

Creation

Properties

Linear Regression Properties

Quantiles — Quantiles vector of values in the range [0,1]

Beta — Linear coefficient estimates numeric matrix

Bias — Estimated bias terms numeric vector

Lambda — Regularization term strength nonnegative scalar

Solver — Objective function minimization technique 'bfgs' | 'lbfgs'

ModelParameters — Parameter values used to train model QuantileLinearParams object

ConvergenceInfo — Convergence information structure array

Predictor Properties

PredictorNames — Predictor variable names cell array of character vectors

CategoricalPredictors — Categorical predictor indices vector of positive integers | []

ExpandedPredictorNames — Expanded predictor names cell array of character vectors

Mu — Predictor means numeric vector | []

Sigma — Predictor standard deviations numeric vector | []

X — Unstandardized predictors numeric matrix | table

Response Properties

ResponseName — Response variable name character vector

Y — Response values numeric vector

ResponseTransform — Response transformation function 'none' | function handle

Other Data Properties

NumObservations — Number of observations positive numeric scalar

RowsUsed — Observations of original training data stored logical vector | []

W — Observation weights numeric vector

Object Functions

Examples

Fit Quantile Linear Regression Model

Version History

See Also

`Quantiles` — Quantiles
vector of values in the range [0,1]

`Beta` — Linear coefficient estimates
numeric matrix

`Bias` — Estimated bias terms
numeric vector

`Lambda` — Regularization term strength
nonnegative scalar

`Solver` — Objective function minimization technique
`'bfgs'` | `'lbfgs'`

`ModelParameters` — Parameter values used to train model
`QuantileLinearParams` object

`ConvergenceInfo` — Convergence information
structure array

`PredictorNames` — Predictor variable names
cell array of character vectors

`CategoricalPredictors` — Categorical predictor indices
vector of positive integers | `[]`

`ExpandedPredictorNames` — Expanded predictor names
cell array of character vectors

`Mu` — Predictor means
numeric vector | `[]`

`Sigma` — Predictor standard deviations
numeric vector | `[]`

`X` — Unstandardized predictors
numeric matrix | table

`ResponseName` — Response variable name
character vector

`Y` — Response values
numeric vector

`ResponseTransform` — Response transformation function
`'none'` | function handle

`NumObservations` — Number of observations
positive numeric scalar

`RowsUsed` — Observations of original training data stored
logical vector | `[]`

`W` — Observation weights
numeric vector