predict

Fit a quantile linear regression model using the 0.25, 0.50, and 0.75 quantiles.

Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a matrix X containing the predictor variables Acceleration, Displacement, Horsepower, and Weight. Store the response variable MPG in the variable Y.

load carbig
X = [Acceleration,Displacement,Horsepower,Weight];
Y = MPG;

Delete rows of X and Y where either array has missing values.

R = rmmissing([X Y]);
X = R(:,1:end-1);
Y = R(:,end);

Partition the data into training data (XTrain and YTrain) and test data (XTest and YTest). Reserve approximately 20% of the observations for testing, and use the rest of the observations for training.

rng(0,"twister") % For reproducibility of the partition
c = cvpartition(length(Y),"Holdout",0.20);

trainingIdx = training(c);
XTrain = X(trainingIdx,:);
YTrain = Y(trainingIdx);

testIdx = test(c);
XTest = X(testIdx,:);
YTest = Y(testIdx);

Train a quantile linear regression model. Specify to use the 0.25, 0.50, and 0.75 quantiles (that is, the lower quartile, median, and upper quartile). To improve the model fit, change the beta tolerance to 1e-6 instead of the default value 1e-4. Use a ridge (L2) regularization term of 1. Adding a regularization term can help prevent quantile crossing.

Mdl = fitrqlinear(XTrain,YTrain,Quantiles=[0.25,0.50,0.75], ...
    BetaTolerance=1e-6,Lambda=1)

Mdl = 
  RegressionQuantileLinear
             ResponseName: 'Y'
    CategoricalPredictors: []
        ResponseTransform: 'none'
                     Beta: [4x3 double]
                     Bias: [17.0004 23.0029 29.5243]
                Quantiles: [0.2500 0.5000 0.7500]

Mdl is a RegressionQuantileLinear model object. You can use dot notation to access the properties of Mdl. For example, Mdl.Beta and Mdl.Bias contain the linear coefficient estimates and estimated bias terms, respectively. Each column of Mdl.Beta corresponds to one quantile, as does each element of Mdl.Bias.

In this example, you can use the linear coefficient estimates and estimated bias terms directly to predict the test set responses for each of the three quantiles in Mdl.Quantiles. In general, you can use the predict object function to make quantile predictions.

predictedY = XTest*Mdl.Beta + Mdl.Bias

predictedY = 78×3

   12.3963   16.2569   19.5263
    5.8328   10.1568   12.6058
   17.1726   20.6398   24.9748
   23.3790   28.1122   31.3617
   17.0036   22.5314   23.0539
   16.6120   17.0713   20.1062
   10.9274   12.3302   13.2707
   14.9130   14.6659   12.7100
   16.3103   17.7497   20.8477
   19.6229   25.7109   30.5389
      ⋮

isequal(predictedY,predict(Mdl,XTest))

ans = logical
   1

Each column of predictedY corresponds to a separate quantile (0.25, 0.5, or 0.75).

Visualize the predictions of the quantile linear regression model. First, create a grid of predictor values.

minX = floor(min(X))

minX = 1×4

           8          68          46        1613

maxX = ceil(max(X))

maxX = 1×4

          25         455         230        5140

gridX = zeros(100,size(X,2));
for p = 1:size(X,2)
    gridp = linspace(minX(p),maxX(p))';
    gridX(:,p) = gridp;
end

Next, use the trained model Mdl to predict the response values for the grid of predictor values.

gridY = predict(Mdl,gridX)

gridY = 100×3

   20.8073   25.4104   29.1436
   20.6991   25.2907   29.0251
   20.5909   25.1711   28.9066
   20.4828   25.0514   28.7881
   20.3746   24.9318   28.6696
   20.2664   24.8121   28.5512
   20.1583   24.6924   28.4327
   20.0501   24.5728   28.3142
   19.9419   24.4531   28.1957
   19.8337   24.3335   28.0772
      ⋮

For each observation in gridX, the predict object function returns predictions for the quantiles in Mdl.Quantiles.

View the gridY predictions for the second predictor (Displacement). Compare the quantile predictions to the true test data values.

predictorIdx = 2;
plot(XTest(:,predictorIdx),YTest,".")
hold on
plot(gridX(:,predictorIdx),gridY(:,1))
plot(gridX(:,predictorIdx),gridY(:,2))
plot(gridX(:,predictorIdx),gridY(:,3))
hold off
xlabel("Predictor (Displacement)")
ylabel("Response (MPG)")
legend(["True values","0.25 predicted values", ...
    "0.50 predicted values","0.75 predicted values"])
title("Test Data")

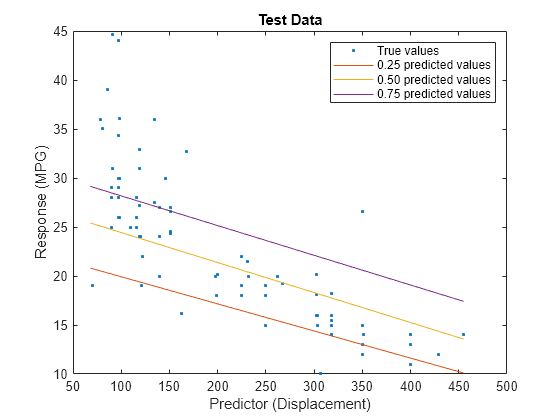
The red line shows the predictions for the 0.25 quantile, the yellow line shows the predictions for the 0.50 quantile, and the purple line shows the predictions for the 0.75 quantile. The blue points indicate the true test data values.

Notice that the quantile prediction lines do not cross each other.

When training a quantile linear regression model, you can use a ridge (L2) regularization term to prevent quantile crossing.

Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Acceleration, Cylinders, Displacement, and so on, as well as the response variable MPG.

load carbig
cars = table(Acceleration,Cylinders,Displacement, ...
    Horsepower,Model_Year,Weight,MPG);

Remove rows of cars where the table has missing values.

cars = rmmissing(cars);

Partition the data into training and test sets using cvpartition. Use approximately 80% of the observations as training data, and 20% of the observations as test data.

rng(0,"twister") % For reproducibility of the data partition
c = cvpartition(height(cars),"Holdout",0.20);

trainingIdx = training(c);
carsTrain = cars(trainingIdx,:);

testIdx = test(c);
carsTest = cars(testIdx,:);

Train a quantile linear regression model. Use the 0.25, 0.50, and 0.75 quantiles (that is, the lower quartile, median, and upper quartile). To improve the model fit, change the beta tolerance to 1e-6 instead of the default value 1e-4.

Mdl = fitrqlinear(carsTrain,"MPG",Quantiles=[0.25 0.5 0.75], ...
    BetaTolerance=1e-6);

Mdl is a RegressionQuantileLinear model object.

Determine if the test data predictions for the quantiles in Mdl.Quantiles cross each other by using the predict object function of Mdl. The crossingIndicator output argument contains a value of 1 (true) for any observation with quantile predictions that cross.

[~,crossingIndicator] = predict(Mdl,carsTest);
sum(crossingIndicator)

ans = 
2

In this example, two of the observations in carsTest have quantile predictions that cross each other.

To prevent quantile crossing, specify the Lambda name-value argument in the call to fitrqlinear. Use a 0.1 ridge (L2) penalty term.

newMdl = fitrqlinear(carsTrain,"MPG",Quantiles=[0.25 0.5 0.75], ...
    BetaTolerance=1e-6,Lambda=0.1);
[predictedY,newCrossingIndicator] = predict(newMdl,carsTest);
sum(newCrossingIndicator)

ans = 
0

With regularization, the predictions for the test data set do not cross for any observations.

Visualize the predictions returned by newMdl by using a scatter plot with a reference line. Plot the predicted values along the vertical axis and the true response values along the horizontal axis. Points on the reference line indicate correct predictions.

plot(carsTest.MPG,predictedY(:,1),".")
hold on
plot(carsTest.MPG,predictedY(:,2),".")
plot(carsTest.MPG,predictedY(:,3),".")
plot(carsTest.MPG,carsTest.MPG)
hold off
xlabel("True MPG")
ylabel("Predicted MPG")
legend(["0.25 quantile values","0.50 quantile values", ...
    "0.75 quantile values","Reference line"], ...
    Location="southeast")
title("Test Data")

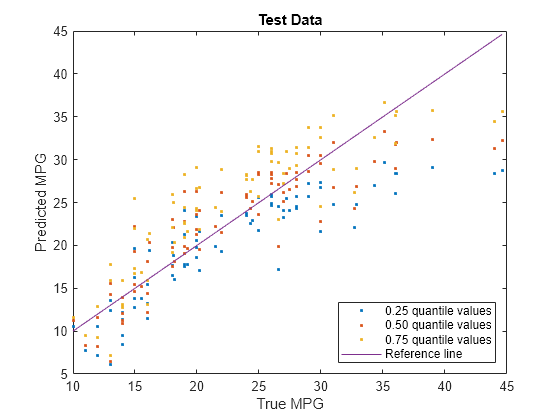
Blue points correspond to the 0.25 quantile, red points correspond to the 0.50 quantile, and yellow points correspond to the 0.75 quantile.